行动装置动力学模型及其应用

根据装甲车辆行动装置模型组成，可以将其看作多刚体系统。多刚体系统分为4个基本部分：部件、约束、作用力和自定义的代数/微分方程。

部件是指任何刚体或集总质量或柔性体等，每个部件列出相应的动力学方程（将力和加速度相联系）和运动学方程（将位置和速度相联系）。

约束是指在系统中对一个（或多个）部件的运动作出限制，每个约束列出一个（或多个）代数约束方程（方程的数目与其限制的自由度数目相同）。

作用力包括两类：其一，体积力，包括重力、电磁力等；其二，接触力，包括除体积力以外的各种外力。

自定义的代数/微分方程：对于一些特殊要求，可直接加入所需的代数/微分方程。

装甲车辆行动装置多体动力学模型的建立，需以大量的各类参数为支撑。建模所需的参数主要分为三类：尺寸参数、质量特性参数和力学特性参数。

尺寸参数是指动力学模型中各零部件的几何形状和定位参数，决定了系统整体与各零部件的空间位置和运动关系。在装甲车辆行动装置动力学模型中，主要有车辆整体的结构形式和外形尺寸，主动轮、负重轮、诱导轮、履带和托带轮的外形尺寸和安装位置等。尺寸参数一般可通过查阅设计资料、图纸和实车测量等方法获得。

质量特性参数是指多体系统中各刚体的质量、质心和转动惯量。在进行多体动力学分析时，各零部件的质量、质心和转动惯量等参数对车辆的动力学性能起决定性作用。

力学特性参数是指扭力轴、减振器等零部件的刚度、阻尼。零部件的力学特性对履带车的通过性、行驶平顺性以及操纵性能具有直接的影响。

1.悬挂系统动力学模型

利用平动弹簧阻尼驱动器和转动弹簧阻尼驱动器等力单元可模拟各种不同结构形式的悬挂系统。装甲车辆悬挂系统采用独立扭杆弹簧及平衡肘式导向机构，建模时采用转动弹簧旋转阻尼器模拟实车悬挂系统。悬挂系统的作用扭矩T计算公式如下：

式中，T0——悬挂系统预张紧扭矩值，N·m；

KT——扭杆弹簧刚度系数，N·m/（°）；

CT——减振器阻尼系数，N·m·s/（°）；

θ——扭杆弹簧扭转角，（°）；

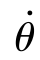——扭转角速度，（°）/s。

2.多刚体系统总体动力学模型

以第一类拉格朗日方程建立多刚体系统总体动力学方程。系统的几何约束方程如下：

对于由两个刚体组成的铰，约束方程如下：

式中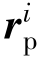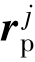， ， ——惯性基中的矢量，分别为刚体i和刚体j连体坐标系统中铰定义点的位置矢量，方向由惯性坐标原点指向铰定义点；

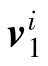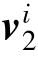，——在刚体i中定义的与铰轴向正交的矢量；

v j——在刚体j中定义的与铰轴向平行的矢量。

刚体i的铰定义点在惯性基XYZ中的位置矢量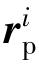计算公式如下：

式中，R i——刚体i连体基原点在惯性基中的位置矢量；

A i——惯性基对刚体i连体基的方向余弦矩阵；(www.xing528.com)

——连体基中由原点指向铰定义点的矢量。

将式（5－11）对时间求一次导数：

即

式中，——刚体i和刚体j在各自连体基中的角速度矢量；

令

式（5－14）可写成

式（5－17）对时间求一次导数：

其中，。

同理，多刚体系统的所有运动副约束方程的雅可比矩阵：

式中，；

系统的动力学方程可写成如下的矩阵形式：

式中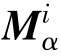，——刚体i的质量阵；

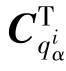——约束方程的雅可比矩阵；

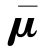——拉格朗日乘子；

——系统的主矢阵、主矩阵。

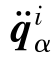由下式定义：

式中，（αi）T——刚体的加速度矢量。

拉格朗日乘子的个数与非独立变量的坐标相等，用s表示。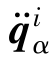的阶数为6n，而方程的未知参数个数为6n＋s，所以必须增加s个方程才能求解。

另有广义质量阵：

可得矩阵：

式中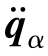，——广义坐标的二阶导数；

Qe＋Qv——广义力矩阵，由装甲车辆行动装置中各零部件之间的相互作用力和铰接点的约束反力构成。

上述方程个数与未知数个数相等，可使用牛顿－拉弗森方法求解该类微分方程组。