1.费用优化的原则
费用优化的目的是使项目的总费用最低优化,应从以下四个方面进行考虑。
(1)在既定工期的前提下,确定项目的最低费用。
(2)在既定的最低费用限额下完成项目计划,确定最佳工期。
(3)在网络图中存在多条关键线路时,若继续进行优化,就需要同时缩短这些线路中某些工作的持续时间。
(4)同时压缩多个并行工作的持续时间时,既要考虑赶工时间的限制,又要考虑这些工作持续时间的时间差数的限制,应取这两个限制的最小值。
2.时间和费用的关系
工程网络计划的工期确定下来后,其所包含的总费用也就确定下来,网络计划所涉及的总费用由直接费和间接费两部分组成。直接费由人工费、材料费和机械费组成,它随工期的缩短而增加,间接费属于管理费用范畴,它随工期缩短而减少。由于直接费随工期缩短而增加,间接费随工期缩短而减小,两者进行叠加,必有一个总费用最少的工期,这就是费用优化所寻求的目标。
间接费用和直接费用与工期的关系如图3-41所示。图中的总费用为直接费用与间接费用叠加而成。总费用曲线在p点为最小费用Cp,所对应的Tp为最优工期。
由于间接费用基本与工期成正线性关系,计算方便,所以在费用优化中,主要分析直接费用与工期的关系,图3-42表示的是直接费用与工期的关系。图中T0和Tn分别为完成工作的最短和正常持续时间,C0和Cn为T0和Tn相应的直接费用。通过图3-42可求出缩短单位时间直接费用的增长率(即费用率)CT:
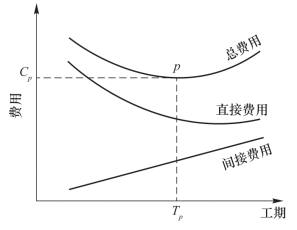
图3-41 费用与工期的关系
![]()
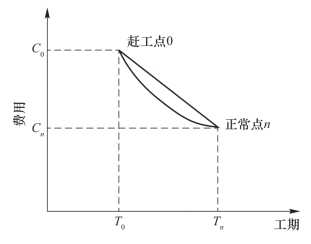
图3-42 直接费用与工期的关系
3.费用优化的步骤
(1)根据各工作正常持续时间,通过计算时间参数确定网络计划的关键线路、总工期以及直接费用和总费用。
(2)在缩短时间限制内,压缩直接费用增长率最小的关键工作持续时间,并计算其直接费用。
(3)计算总费用,与上次优化结果比较,若大于上次优化结果的总费用,则停止优化,说明上次结果为最优,否则,重复上一步骤,寻求总费用最低的方案。
4.费用优化示例
【例3-6】 某工程双代号网络计划如图3-43所示。若间接费用每天为1100元,直接费用资料见表3-7。试寻求工期最短且总费用最少的网络计划的费用优化方案。
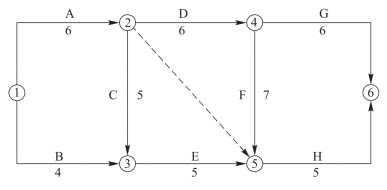
图3-43 某工程双代号网络计划(https://www.xing528.com)
表3-7 直接费用资料
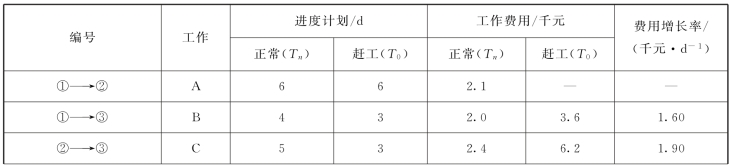
续表

【解】 根据图3-43的正常持续时间,计算出网络图的总工期为24d;关键线路为①→②→④→⑤→⑥,如图3-44所示;所需总费用为
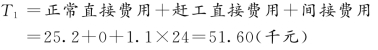
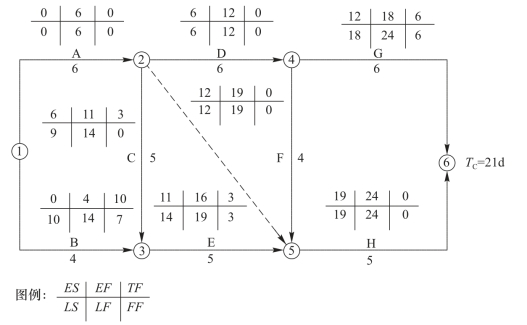
图3-44 某工程双代号网络计划时间参数计算
第1次压缩:由表3-7可知,关键工作A、D、F、H工作的直接费用增长率最小者为F工作(0.65千元/d)。由图3-44可知,除了关键工作外,其余工作的总时差的最小值为3d,而F工作可压缩4d。故只能压缩F工作3d,才能使原关键线路不变。压缩F工作3d后,重新计算总工期、总时差和总费用,计算网络图如图3-45所示。
由图3-45可知,总工期为21d,除了原关键线路不变外,又增加了一条①→②→③→⑤→⑥的关键线路。那么,所需的总费用T2为
![]()
由于T2=50.25千元,小于T1=51.60千元,故还可以继续压缩。
第2次压缩:若再缩短工期,还有5种方式可供选择,见表3-8。
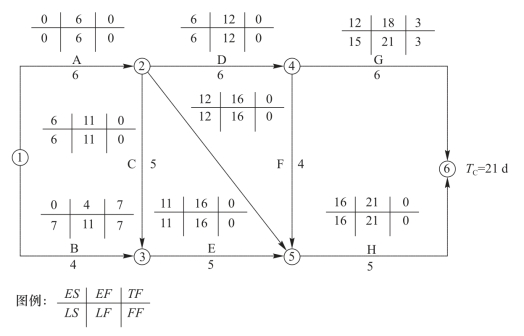
图3-45 第1次压缩后某工程双代号网络计划时间参数计算
表3-8 缩短工期的几种方式
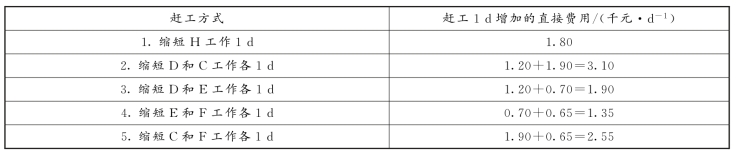
由表3-8可知,选择赶工方式4,所增加的直接费用最低,为1.35千元/d。而F工作仅有1d可赶工,故采取E、F各缩短1d方式,重新计算网络图的时间参数如图3-46所示。经过缩短E、F工作各1d后,总工期为20d,关键线路不变。那么,所需总费用T3为
![]()
由于T3=50.5千元,大于T2=50.25千元,因此,经过第1次压缩后,便使原网络计划达到了工期最短、费用最少的目的,实现了费用优化。此时,最短总工期为21d,最少总费用为50.25千元。
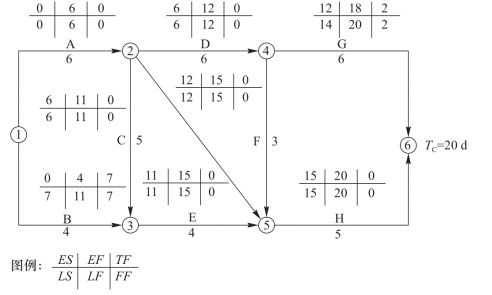
图3-46 第2次压缩后工程双代号网络计划时间参数计算
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




