给水管网的计算就是决定管径和供水时的水头损失。为了确定管径,就必须先确定设计流量。新建和扩建的城市管网按最高时用水量计算,据此求出所有管段的直径、水头损失、水泵扬程和水塔高度(当设置水塔时)。并在此管径基础上按其他用水情况,如消防时、事故时、对置水塔系统在最大转输时各管段的流量和水头损失,从而可以知道按最高用水时确定的管径和水泵扬程能否满足其他用水时的水量和水压要求。
对于改建和扩建的管网,因现有管线遍布在街道下,不但管线太多,而且不同管径交接,计算时比新设计的管网较为困难。其原因是由于生活和生产用水量不断增长,水管结垢或腐蚀等,使计算结果易于偏离实际,这时必须对现实情况进行调查研究,调查用水量、节点流量、不同材料管道的阻力系数和实际管径、管网水压分布等,才能使计算结果接近于实际。
1.管网图形的性质与简化
(1)管网图形的性质。给水管网是由管段和节点构成的有向图,管网图形中每个节点通过一条或多条管段与其他节点相连接。
1)节点。有集中流量进出、管道合并或分叉以及边界条件发生变化的地点,如图2.13所示的1,2,3,…,8节点。
2)管段。两个相邻节点之间的管道管线:顺序相连的若干管段,如图2.13所示的管段3~6。
3)环。起点与终点重合的管线,如图2.13所示的2~3~6~5~2。
a.基环。不包含其他环的环,如图2.13所示的环2~3~6~5~2,即图中的环Ⅰ。
b.大环。包含两个或两个以上基环的环,如图2.13所示的环Ⅰ、环Ⅱ合成的大环2~3~4~7~6~5~2。
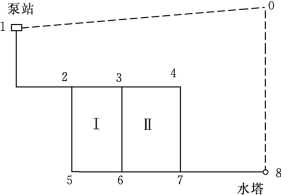
图2.13 干管网的组成
c.虚环。多水源的管网,为了计算方便,有时将两个或多个水压已定的水源节点(泵站、水塔等)用虚线和虚节点0连接起来,也形成环,因实际上并不存在,所以称为虚环,如图2.13所示的1~0~8~7~4~3~2~1大环。
(2)管网图形的简化。
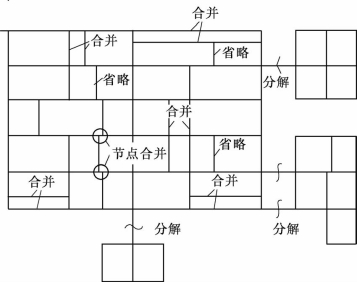
图2.14 管网简化
1)简化目的及原则。由于给水管线遍布在街道下,不但管线很多而且管径差别很大,若计算全部管线,实际上既无必要,也不大可能。对于新设计的管网,因为定线和计算仅限于干管网,所以管网设计计算相对简单,而对城镇管网的现状核算以及管网的扩建或改建往往需要将实际的管网加以简化,保留主要的干管,略去一些次要的、水力条件影响较小的管线,使简化后的管网基本上能反映实际用水情况,大大减轻计算工作量。通常管网越简化,计算工作量越小。但过分简化的管网,计算结果难免与实际用水情况的差别增大。所以,管网图形简化是保证计算结果接近于实际情况的前提下,对管线进行的简化。
2)简化方法。在进行管网简化时,应先对实际管网的管线情况进行充分了解和分析,然后采用分解、合并、省略等方法进行简化。图2.14为某城市管网管线布置,共计42个环。
a.分解。只有一条管线连接的两个管网,可以把连接管线断开,分解成为两个独立的管网;有两条管线连接的分支管网,若其位于管网的末端且连接管线的流向和流量可以确定时,也可以进行分解;管网分解后即可分别计算。
b.合并。管径较小、相互平行且靠近的管线可考虑合并。如管线交叉点很近时,可以将其合并为同一交叉点。相近交叉点合并后可以减少管线数目,使系统简化。在给水管网中,为了施工方便和减小水流阻力,管线交叉处往往用两个三通代替四通(实际工程中很少使用四通),不必将两个三通认为是两个交叉点,仍应简化为四通交叉点。
c.省略。管线省略时,首先略去水力条件影响较小的管线,即省略管网中管径相对较小的管线。管线省略后的计算结果是偏于安全的,但是由于流量集中,管径增大,并不经济。
2.沿线流量
城市给水管网的干管和分配管上,承接了许多用户,沿线配水情况比较复杂,既有工厂、机关、学校、医院、宾馆等大用户,其用水流量称为集中流量,又有数量很多、但用水量较小的居民用水、浇洒道路或绿化用水等沿线流量,以致不但沿线所接用户很多,而且用水量变化也很大。干管的配水情况如图2.15所示。
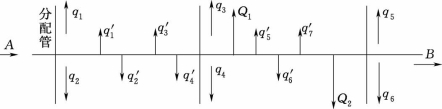
图2.15 干管配水情况
从图2.15中可以看出,干管除供沿线两旁为数较多的居民生活用水q′1、q′2、q′3、…外,还要供给分配管流量q1、q2、q3等,还有可能给少数大用水户供应集中流量Q1、Q2、Q3、…。由于用水点多,用水量经常变化,所以按实际情况进行管网计算是非常繁杂的,而且在实际工程中也无必要。所以,为了计算方便,常采用简化法——比流量法,即将除去大用户集中流量以外的用水量均匀地分配在全部有效干管长度上,由此计算出的单位长度干管承担的供水量。比流量法有长度比流量和面积比流量两种。
(1)长度比流量。所谓长度比流量法是假定沿线流量q′1、q′2、…均匀分布在全部配水干管上,则管线单位长度上的配水流量称为长度比流量,记为qs[L/(s·m)],可按下式计算:
![]()
式中 Q——管网总用水量,L/s;
∑Qi——工业企业及其他大用户的集中流量之和,L/s;
∑L——管网配水干管总计算长度,m;单侧配水的管段(如沿河岸等地段敷设的只有一侧配水的管线)按实际长度的一半计入;双侧配水的管段,计算长度等于实际长度;两侧不配水的管线长度不计(即不计穿越广场、公园等无建筑物地区的管线长度)。
比流量的大小随用水量的变化而变化。因此,控制管网水力情况的不同供水条件下的比流量(如在最高用水时、消防时、最大转输时的比流量)是不同的,须分别计算。另外,若城市内各区人口密度相差较大时,也/应根据各区的用水量和干管长度,分别计算其比流量。
长度比流量按用水量全部均匀分布在干管上的假定来求比流量,忽视了沿管线供水人数和用水量的差别,存在一定的缺陷,因此计算出来的配水量可能和实际配水量有一定差异。为接近实际配水情况,也可按面积比流量法计算。
(2)面积比流量。假定沿线流量q′1、q′2、…均匀分布在整个供水面积上,则单位面积上的配水流量称为面积比流量,记作qA[单位L/(s·m2)],按下式计算:
![]()
式中 ∑A——给水区域内沿线配水的供水面积总和,m2;
其余符号意义同前。
干管每一管段所负担的供水面积可按分角线或对角线的方法进行划分,如图2.16所示。在街坊长边上的管段,其单侧供水面积为梯形;在街坊短边上的管段,其单侧供水面积为三角形。
面积比流量因考虑了管线供水面积(人数)多少对管线配水流量的影响,故计算结果更接近实际配水情况,但计算复杂。当供水区域的干管分布比较均匀,管距大致相同时,两者计算结果相差很小,采用长度比流量简便。当供水区域内各区卫生设备情况或人口密度差异较大时,各区比流量应分别计算。同一管网,比流量大小随用水流量变化而变化,故管网在不同供水条件下的比流量需分别计算。

图2.16 供水面积划分
由比流量qs、qA可计算出各管段的沿线配水流量即沿线流量,记作qy,则任一管段的沿线流量qy(单位L/s)可按下式计算:
![]()
或
![]()
式中 Li——该管段的计算长度,m;
Ai——该管段所负担的供水面积,m2。
3.节点流量

图2.17 转输流量示意图
管网中任一管段的流量,包括两部分:一部分是沿本管段均匀泄出供给各用户的沿线流量qy,流量大小沿程直线减小,到管段末端等于零;另一部分是通过本管段流到下游管段的流量,沿程不发生变化,称为转输流量qzs。从管段起端A到末端B管段内流量由qzs+qy变为qzs,如图2.17所示。对于流量变化的管段,难以确定管径和水头损失,因此,需对其进一步简化。简化的方法是化渐变流为均匀流,即以变化的沿线流量折算为管段两端节点流出的流量,亦即节点流量。全管段引用一个不变的流量,称为折算流量,记为qif,使它产生的水头损失与实际上沿线变化的流量产生的水头损失完全相同,从而得出管线折算流量的计算公式为
![]() (https://www.xing528.com)
(https://www.xing528.com)
式中 α——折减系数,通常统一采用0.5,即将管段沿线流量平分到管段两端的节点上。
因此管网任一节点的节点流量为
![]()
即管网中任一节点的节点流量qi等于与该节点相连各管段的沿线流量总和的一半。
当整个给水区域内管网的比流量qcb或qmb相同时,由式(2.25)和式(2.26)可得节点流量计算式(2.28)的另一种表达形式:
![]()
或
![]()
式中 ∑Li——与该节点相连各管段的计算长度之和,m;
∑Ai——与该节点相连各管段所负担的配水面积之和,m2。
城市管网中,工企业等大用户所需流量,可直接作为接入大用户节点的节点流量。工业企业内的生产用水管网,水量大的车间用水量也可直接作为节点流量。
这样,管网图上各节点的流量包括由沿线流量折算的节点流量和大用户的集中流量。大用户的集中流量可以在管网图上单独注明,也可与节点流量加在一起,在相应节点上注出总流量。一般在管网计算图的各节点旁引出细实线箭头,并在箭头的前端注明该节点总流量的大小。
4.管段流量
管网各管段的沿线流量简化成各节点流量后,可求出各节点流量,并把大用水户的集中流量也加于相应的节点上,则所有节点流量的总和,便是由二级泵站送来的总流量,即总供水量。按照质量守恒原理,每一节点必须满足节点流量平衡条件:流入任一节点的流量必须等于流出该节点的流量,即流进等于流出。
若规定流入节点的流量为负,流出节点为正,则上述平衡条件可表示为
![]()
式中 qi——节点i的节点流量,L/s;
qij——连接在节点i上的各管段流量,L/s。
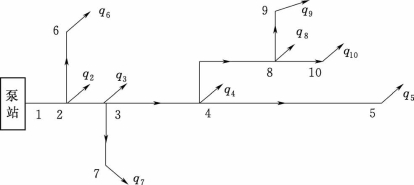
图2.18 枝状管网管段流量计算
依据式(2.31),用二级泵站送来的总流量沿各节点进行流量分配,所得出的各管段所通过的流量,就是各管段的计算流量。
在单水源枝状管网中,各管段的计算流量容易确定。从配水源(泵站或水塔等)供水到各节点只能沿一条管路通道,即管网中每一管段的水流方向和计算流量都是确定的。每一管段的计算流量等于该管段后面(顺水流方向)所有节点流量和大用户集中用水量之和。因此,对于枝状管网,若任一管段发生事故,该管段以后地区就会断水。
如图2.18所示的一枝状管网,部分管段的计算流量为

5.管径计算
确定管网中每一管段的直径是输水和配水系统设计计算的主要课题之一。管段的直径应按分配后的流量确定。因为
![]()
所以在设计中,各管段的管径按下式计算:

式中 q——管段流量,m3/s;
A——水管断面面积,m2;
D——管段直径,m;
v——流速,m/s。
由式(2.33)可知,管径不但和管段流量有关,而且还与流速有关。因此,确定管径时必须先选定流速。
为了防止管网因水锤现象而损坏,在技术上最大设计流速限定在2.5~3.0m/s范围内;在输送浑浊的原水时,为了避免水中悬浮物质在水管内沉积,最低流速通常应大于0.60m/s,由此可见,在技术上允许的流速范围是较大的。因此,还需在上述流速范围内,根据当地的经济条件,考虑管网的造价和经营管理费用,来选定合适的流速。
从式(2.33)可以看出,流量一定时,管径与流速的平方根成反比。如果流速选用的大一些,管径就会减小,相应的管网造价便可降低,但水头损失明显增加,所需的水泵扬程将增大,从而使经营管理费(主要指电费)增大,同时流速过大,管内压力高,因水锤现象引起的破坏作用也随之增大。相反,若流速选用小一些,因管径增大,管网造价会增加。但因水头损失减小,可节约电费,使经营管理费降低。因此,管网造价和经营管理费(主要指电费)这两项经济因素是决定流速的关键。按一定年限t(称为投资偿还期)内,管网造价和经营管理费用之和为最小的流速,称为经济流速,以此来确定的管径,称为经济管径。
若管网造价为C,每年的经营管理费用为M,包括电费M1和折旧、大修费M2,因M2和管网造价有关,故可按管网造价的百分数计,表示为p%C,那么在投资偿还期t年内,总费用为
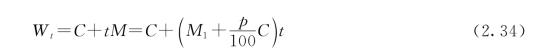
式中 p——管网的折旧和大修率,以管网造价的百分比计。
式(2.34)除以投资偿还期t,则得年折算费用W:


图2.19 流速和费用的关系
总费用W曲线的最低点表示管网造价和经营管理费用之和为最小时的流速,称为经济流速ve,如图2.19所示。
各城市的经济流速值应按当地条件,如水管材料和价格、施工条件、电费等来确定,不能直接套用其他城市的数据。另外,管网中各管段的经济流速也不一样,须随管网图形、该管段在管网中的位置、该管段流量和管网总流量的比例等决定。因为计算复杂,有时简便地应用“界限流量表”确定经济管径,见表2.1。
表2.1 界限流量表

由于实际管网的复杂性,加上情况在不断地变化,例如,流量在不断增加,管网逐步扩展,诸多经济指标如水管价格、电费等也随时变化,要从理论上计算管网造价和年管理费用相当复杂且有一定难度。在条件不具备时,设计中也可采用由各地统计资料计算出的平均经济流速来确定管径,得出的是近似经济管径,见表2.2。
表2.2 平均经济流速

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




