1.1.2.1 沿程水头损失计算
给水排水管道的沿程水头损失常用谢才公式计算，其形式为
式中 hf——沿程水头损失，m；
v——过水断面平均流速，m/s；
C——谢才系数；
R——过水断面水力半径，即过水断面面积除以湿周，m，圆管满流时R=0.25D（D为圆管直径）；
l——管渠长度，m。
对于圆管满流，沿程水头损失也可用达西公式计算：
式中 D——圆管直径，m；
g——重力加速度，m/s2；
λ——沿程阻力系数，λ=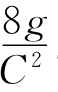
。
沿程阻力系数或谢才系数与水流流态有关，一般只能采用经验公式或半经验公式计算。目前国内外较为广泛使用的主要有舍维列夫公式、海曾-威廉公式、柯尔勃洛克-怀特公式和巴甫洛夫斯基等公式，其中，国内常用的是舍维列夫公式和巴甫洛夫斯基公式。
1.舍维列夫公式
舍维列夫公式根据他对旧铸铁管和旧钢管的水力实验（水温10℃），提出了计算紊流过渡区的经验公式。
当v≥1.2m/s时
当v＜1.2m/s时
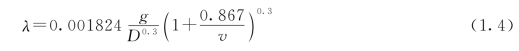
将式（1.3）、式（1.4）代入式（1.2）分别得
当v≥1.2m/s时
当v＜1.2m/s时
2.海曾-威廉公式
海曾-威廉公式适用于较光滑的圆管满管紊流计算：
式中 q——流量，m3/s；
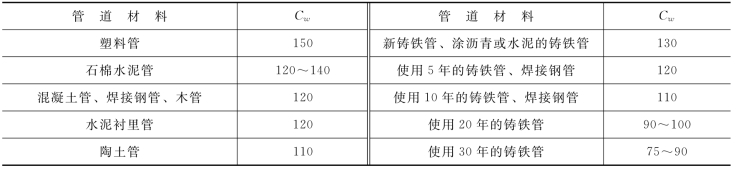
Cw——海曾-威廉粗糙系数，其值见表1.1；
其余符号意义同式（1.2）。
表1.1 海曾-威廉粗糙系数Cw值
将式（1.7）代入式（1.2）得
3.柯尔勃洛克-怀特公式
柯尔勃洛克-怀特公式适用于各种紊流：
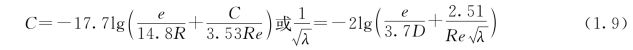
式中 Re——雷诺数，
（其中υ为水的动力黏滞系数，和水温有关，单位为m2/s）；
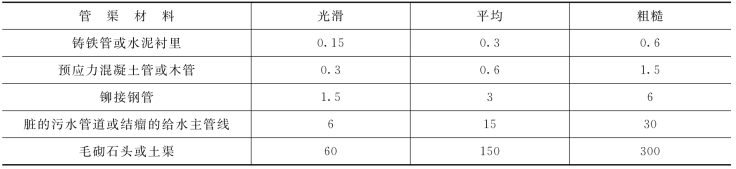
e——管壁当量粗糙度，m，由实验确定，常用管材的e值见表1.2。
表1.2 常用管渠材料内壁当量粗糙度e值 单位：mm
(www.xing528.com)
续表
该式适用范围广，是计算精度最高的公式之一，但运算较复杂，为便于应用，可简化为直接计算的形式：
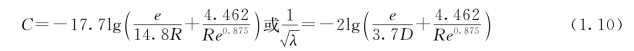
4.巴甫洛夫斯基公式
巴甫洛夫斯基公式适用于明渠流和非满流管道的计算，公式为
其中
式中 nb——巴甫洛夫斯基公式粗糙系数，见表1.3。
表1.3 常用管渠材料粗糙系数nb值
将式（1.11）代入式（1.2）得
5.曼宁公式
曼宁公式是巴甫洛夫斯基公式中y=1/6时的特例，适用于明渠或较粗糙的管道计算：
式中 n——粗糙系数，与式（1.12）中nb相同，见表1.3。
将式（1.13）代入式（1.1）得
1.1.2.2 局部水头损失计算
局部水头损失用下式计算：
式中 hj——局部水头损失，m；
ζ——局部阻力系数，见表1.4。
表1.4局部阻力系数ζ
在管网系统中，各种配件、附件或设施种类数量繁多，局部水头损失计算起来十分繁复，所以为了简化计算，可以将局部水头损失等效于一定长度的管道（称为当量管道长度）的沿程水头损失，从而可以与沿程水头损失合并计算。
设某管道直径为d，管道上的局部阻力设施的阻力系数为ζ，令其局部水头损失与当量管道长度的沿程水头损失相等，则有
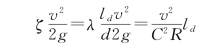
经简化得
式中 ld——当量管道长度，m。
【案例1.1】 已知某管道直径d=800mm，管壁粗糙系数n=0.0013，管道上有2个45°和1个90°弯头，2个闸阀，2个直流三通，试计算当量管道长度ld。
【解】 查表1.4，该管道上总的局部阻力系数：
ζ=2×0.4+1×0.9+2×0.19+2×0.1=2.28
采用曼宁公式计算谢才系数：
求得当量管道长度为
在实际中，室外给水排水管网中的局部水头损失一般不超过沿程水头损失的5%，因和沿程水头损失相比很小，所以在管网水力计算中，常忽略局部水头损失的影响，不会造成大的计算误差。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
