西南地区泥石流灾害损失测度及救灾管理研究

巨灾债券定价是整个巨灾债券发行、流通的最关键因素之一，也是能否成功通过保险风险证券化顺利将巨灾风险转嫁至资本市场的决定性因素之一。本章主要研究定价问题。巨灾债券不是传统的金融证券，具有显著的保险特征，但又不是单纯的保险，因此它的定价无法用常规的债券定价方法或者保险定价方法进行定价。本节主要探讨巨灾债券现有的定价模型，并针对现有定价模型的不足进行改进。

（1）巨灾债券定价模型概述

巨灾债券是保险风险证券化中发行时间最早、发行量最大、发行范围最广、交易最为活跃的证券产品，其主要运行的核心环节包括两个：其一，将承保现金流转化为标准化的可交易债券；其二，通过交易债券将巨灾风险从保险市场转移到资本市场[77]。合理的风险定价对于现金流转化环节和风险转嫁环节成功运行至关重要。因此，定价问题往往是巨灾债券研究的核心。巨灾债券定价属于金融保险研究的前沿领域，现有定价技术还没有统一的规范和标准，总体上还不太成熟。

巨灾债券的研究者主要是金融经济研究员和保险精算师。因此，从这两个不同的行业和职业角度出发，现有的巨灾债券定价模型大致分为两类：金融定价模型和损失精算模型。金融定价模型包含以Cox和Pedersen（2000）[78]、和李永（2013）[79]等为代表的均衡定价模型和以Lee与Yu（2002）[80]、Vaugirard[81]（2003）、Lai（2014）[82]为代表的无套利模型。从保险精算的角度下分析，巨灾债券定价模型主要包含Kreps模型[83]，LFC模型[84]-[86]，Wang转换模型[87]-[89]， Christofides模型和Wang两因素转换模型[90]等。谢世清在《巨灾保险连接证券》中比较了上述几类精算巨灾债券定价模型的精度、优缺点等特征[86]，为相关研究者提供了重要的参考意见。

①金融定价模型。

金融定价模型可划分为均衡定价模型和无套利模型，分别以Cox&Pedersen均衡定价模型和Vaugirad模型为代表。

（a）Cox & Pedersen均衡定价模型。

Cox和Pedersen（2000）认为由于巨灾风险与金融市场潜在变量不相关的事实使得不完全市场定价比在一个风险显著相关的市场进行定价更简单，并提出了代表性的均衡定价模型[78]。该模型的总体思路在于：首先建立无巨灾风险下的支付结构模型；然后，评估巨灾风险大小；最后，将巨灾风险模块与利率变动的支付结构模型相结合进行定价。

债券息票只有一个可能的违约原因——特定的巨灾。假设巨灾债券面值为1 ，债券以每期c的利率开始支付。如果债券存续期间未发生巨灾或者未达到触发机制的要求，连续支付T期，并且最后一期的支付为1+c。如果在债券存续期间发生了一场巨灾且损失达到触发机制的要求，债券就会支付部分息票，并在此期间偿还部分本金。部分支付被假定为以比例f(0＜f＜1)进行支付，因此如果发生了灾难，在周期结束时支付的费用为f(1+c)。

假设金融投资市场中存在一个风险中性的概率测度Q，假设一笔投资，在投资期内存在T次支付，每次支付的金额不确定，记为{c (k )|k=1,2,3…,T }。那么，在投资期的初始时刻（记为0时刻）的不确定的现金流{c (k )|k=1,2,3…,T }的价格由概率测度Q的期望给出：

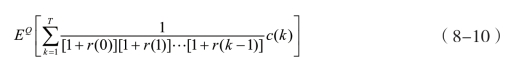
其中，{r (k )|k=1,2,3…,T }是一期的利率随机过程。如果投资证券为面值为1的0息票债券，那么该0息票债券的价格(0,)nP为：

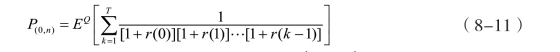
不妨以τ表示巨灾首次发生的时间，如果巨灾发生，τ∈{1,2… T }，如果巨灾不发生，τ∉{1,2 …T }或者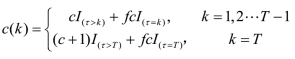。对于本金保障的巨灾债券，现金流支付如下所示：

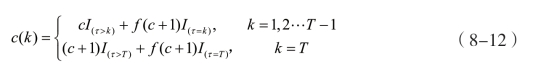
其中，I为指示函数。

对于一种只有在风险中才有现金流回报的巨灾债券，到期时本金得以保证，将（8-12）中的f(1+c)用fc替换，同时调节τ=T以反映本金的偿还状况：

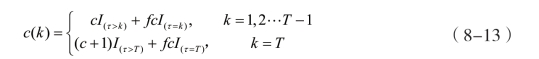
根据Cox和Pedersen（2000）的观点：假设在一个无套利的投资市场中交易巨灾风险债券，风险中性价值测度为Q，巨灾发生时刻与测度Q下的期限结构不相依，联系（8-11）、（8-12）可得0时刻由巨灾债券提供的现金流的现值（巨灾债券发行价格）如等式（8-14）所示。

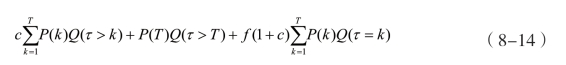
其中，Q(τ＞k)表示在风险中性测度的条件下，前k个时期巨灾未发生的概率，其余以此类推。

（b）Vaugirad模型。

Vaugirad模型证明即使在不完全市场和原始状态变量存在的基础下，巨灾债券无套利定价是存在的。巨灾债券具有一旦触发机制被触发就会被扣除利息和本金的特征，因此债券定价严重依赖于随机变量“首次触发时间”的分布[91]。本文对Vaugirad定价模型进行简要介绍，同时对Vaugirad定价模型进行小幅度的改进，有兴趣读者可参考Vaugirad（2003）[81]、Nowak（2012）[92]以及Nowak（2013）[93]。

设P为巨灾风险发生的概率测度，市场无风险利率波动为CIR型，即无风险利率波动满足以下微分方程：

其中，a (b-r (t))为无风险利率的漂移项，a, b为常数，σ为波动率，Wt为标准布朗运动。同时，假设损失指数是一个跳跃扩散过程，其扩散状态描述如下：

其中，tI表示t时刻的损失指数，用以反映灾害风险导致损失的情况；()tμ为漂移项，2σ为波动项；2()W t为标准布朗运动；tN为服从参数()tη的Poisson过程，它表示单位时间内的跳跃次数（灾害发生次数）；ttJ dN是一个复合Poisson过程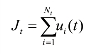，表示跳跃幅度，表示次灾害的累计损失程度，ui(t)为t时刻发生的Nt次灾害中，第i次的损失情况，iu独立同分布，且分布为()P P=·。根据式（8-16）可知，损失指数的变化可分解为巨灾未发生情况的期望变化()tμ、不可预期的变化2()W t以及巨灾发生产生的变化ttJ dN。损失指数的前两部分变化与金融市场风险有关，也是可以通过国债等无风险债券进行复制或者重现，由此，便解决两个问题：跳跃过程的无交易风险指数与市场的不完全性[94]。

Vaugirad（2003）认为，根据上述定义的一个或有权益IC存在一个定义明确的套利定价，如下所示：

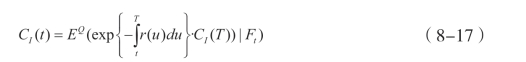
其中，Q是由定义在1()W t和2()W t生成的σ代数构造的等价鞅测度，它刻画了风险中性假定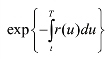，为贴现因子。特别的，当0时刻时，或有债权的定价（发行价格）为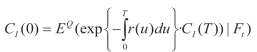：。I与r的取值由有以下（8-18）及（8-19）动态方程决定：

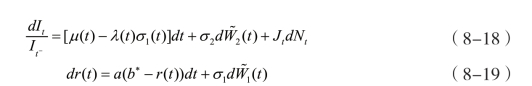
其中，λ(t)为市场风险的价格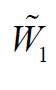，与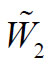分别为W1和W2对应等价鞅测度Q的标准布朗运动，b*=b-λ1σ1/a ，-λ1则刻画了无风险债券的风险溢价。与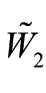以及b*=b-λ1σ1/a 可由Girsanov 定理推导出，详细请查阅文献Vaugirad（2003）。

②损失精算定价模型。

与上述金融定价理论不同，精算定价方法更注重于损失实务，可操作性高于金融定价方法，但是缺乏严密、系统的理论支撑。损失精算定价模型主要包含LFC模型，Wang转换模型，Christofides模型和Wang两因素转换模型等。

（a）LFC模型。

LFC模型，是Kreps再保险定价模型[83]的拓展，由美国Lane Financial公司总裁Morton Lane根据再保险定价和市场上流通的巨灾债券市场价格提出来的。Lane认为，巨灾债券的价格应该有期望损失EL（Expected loss，EL）和超额收益EER（Expect excess return，EER）两部分构成[84]。Lane（1999）将巨灾发生的概率视为“第一单元损失概率”PFL（Probability of the first dollar loss ，PEL），除非损失不发生，否则它等于所有潜在可能的风险损失概率总和，即PEL=，其中，pi＞0，p0 ≥0[85]。CEL是指一次灾害发生造成损失规模的期望值。Lane根据Cobb-Douglas生产函数来计算EER。因此券定价如式（8-20）所示。

其中，,α β分别代表了债券价格对于PEL和CEL的弹性，即敏感程度。,α β可以通过市场上巨灾债券的数据估算。

（b）Wang转换模型。

Wang转换模型定价核心在获取转换后的巨灾风险损失分布。将市场交易中的巨灾债券的价格对巨灾风险进行转换调整，根据转化获得更加精确的巨灾风险损失分布，然后根据转换后的损失分布结合损失期望定价模型进行债券定价。假设S (x)=p{X ＞x}表示一个生存函数概率测度，表示巨灾损失X超过x的概率。即为期望损失。（再）保险保费厘定时，往往会根据风险范围、层级设置不同层级的费率，那么每一层级风险以及对应的期望损失（净保费）分别如式（8-21）和式（8-22）所示。

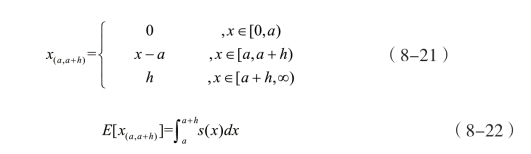
根据黎曼积分的定义，当h很小时，E[X(a,a+h)]≈s (a )·h ，则存在以下关系：

假设实际观测价格为，由于包含期望损失部分和风险溢价部分，因此。一般而言，Shape比例能够较好地模拟巨灾风险正态分布的损失风险[86]，但是由于巨灾风险的偏态和厚尾使得Shape比例不能直接用于巨灾债券定价。因此，Wang（2002）提出（8-24）的转换，将Shape比例运用范围拓展到有偏斜分布的风险损失上。

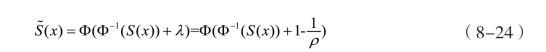
其中，φ为标准正态分布的分布函数，()xS为损失分布，为风险厌恶水平。因此，根据式（8-21）和（8-24），巨灾债券的定价为式（8-25）。

（c）Christofides模型。

Christofides模型是基于Wang转换模型基础上提出来的。Christofides假定巨灾债券支付无风险利率来补偿债券持有者持有债券，同时附加风险溢价来补偿灾害风险。生存函数曲线()S x，曲线下方的面积EL=为巨灾债券的期望损失，比例风险转换函数，因此与S (x)之间的面积即为巨灾债券的风险溢价或者期望超额收益率EER。PE为扣减的本金，PFL为第一美元损失的概率。

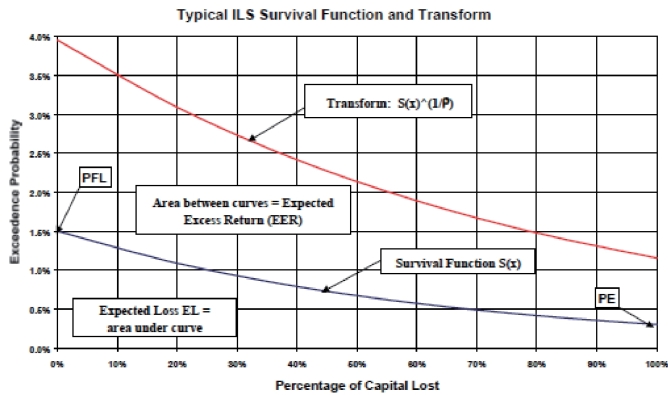
图8-3　生存函数风险厌恶水平下的Wang转换后的生存函数曲线

资料来源：Christofides（2004）

Christofides用指数衰减函数来刻画生存函数，即S (x)=αe-βx ，其中α ,β为未知待估参数。分别令x=0和1，第一美元损失的概率以及本金扣减的概率分别为S(0)=α,S(1)=αe-β，在不考虑风险厌恶水平的条件下，期望损失如式（8-26）所示。

风险厌恶水平ρ根据已发行的债券数据来计算。因此，在 ,,α β ρ已知的条件下，Christofides定价模型如下所示：

如果β足够小，式（8-27）可以近似为下式：

如果将期望损失EL表示为第一美元损失的概率PFL和条件期望损失CEL的面积，那么式（8-27）可以表达为式（8-28）。

（d）Wang两因素转换模型。

Wang转换模型是建立在风险损失分布已知的条件上的。但是由于我们难以全面地了解风险分布，只能经过有限的数据推断分布特征，因此，参数的不确定性始终存在。因此，Wang（2004）考虑了Wang转换模型的缺点，用t分布来代替正态分布来调整风险的厚尾性特征。调整过程如下所示：

其中，T (x)为t分布函数，Φ-1为标准正态分布函数的逆函数，λ为Shape率。根据式（8-29），不同损失层次的巨灾债券定价如式（8-30）所示。

（e）四种巨灾债券定价模型比较。

上文中对损失保险精算模型进行简要介绍，并对上述模型进行简单的比较。四者共同点主要体现在模型的根本形式和都考虑了损失风险的厚尾性特征。

从模型的根源上看，LFC模型、Wang转化模型、Christofides模型和Wang两因素转换模型都是沿袭了保险业的保费计算模型，即巨灾债券的价格视为期望损失和风险溢价的合计。从顺序上看，四个模型具有一定的顺延性和继承性，是一个不断改进和更新的过程。

从厚尾性对巨灾债券定价的影响上看，四个模型都不同程度地考虑厚尾性对巨灾债券定价的影响。

不同点在于模型性质、度量指标、精确程度和缺陷等方面。

首先，对于模型性质，LFC完全属于实证型保险定价的方法，是从精算的角度出发，对巨灾风险和市场特征的归纳，缺乏理论角度的分析。而另外三个模型则不同程度地考虑了巨灾风险厌恶水平以及如何从资本风险和保险风险理论角度来刻画风险溢价。

其次，从风险度量指标上看，LFC采用条件期望损失CEL来衡量巨灾风险损失，Wang转换模型和Christofides模型则是考虑资本市场上的巨灾风险厌恶水平，Wang两因素模型则是考虑从概率变化以及参数不确定性两个方面来描述巨灾风险。

再次，就精确程度而言，田玲（2006）[68]、谢世清（2011）[86]比较结果表明：Wang两因素转换模型精度最高，其次是Wang转换模型，再次是Christofides模型，最后是LFC模型。

最后，从缺陷上看，LFC模型不考虑资本市场周期和巨灾风险的季节性变化趋势；Wang的巨灾风险厌恶水平估计十分困难；Christofides模型对于参数不确定性的分析比较欠缺；Wang两因素转换模型同时考虑参数不确定性和风险厌恶水平，计算复杂，技术模块实现困难。

巨灾债券的定价属于相对前沿的领域，已然成为一个研究热点，其主流方法主要分为金融定价法和损失精算定价法。其中，金融定价法在国外金融领域比较常见，它注重经济金融理论的支撑以及严密的数学推导，正因为追求其理论推导的完美性导致假设限制条件过于严苛，进而使得定价模型复杂，实用性不足。损失精算定价模型因更注重于损失实务，可操作性更高而被广泛保险精算师使用，但是该方法没有形成系统的理论，并且缺少深入、严密、系统的研究。

（2）传统巨灾损失模型改进

①传统灾害损失分布的缺陷。

大多数定价模型是以风险正态分布或者广义上的对称分布为基础的。但是，经验数据表明，灾害风险损失具有显著右偏、厚尾特征。尽管巨灾次数占灾害次数比重较小，但是巨灾一旦发生却极易导致保险公司破产。保险中常用的损失分布，如Gamma、logNormal、Weibull分布，都难以精确地拟合具有厚尾性的巨灾风险。相比较，极值理论（Extreme value theory，EVT）在分析极端损失中却能取到较好的效果。极值理论建模分为两种EVT模型和POT（Peaks Over Threshold，POT）模型。EVT模型提供了一套估计极大值的方法，但是模拟所有的极大值导致大量的数据浪费，尤其在大量数据不可获得的条件下，该方法的运用十分受限。相比，POT模型在分析极端数据时有更好的效果，它侧重于对随机变量超出某个较大阈值的超出量建模，能够更好地模拟随机变量超过某个阈值的数据分布的尾部特征。

但是，POT模型只对超阈值数据的超出量建模，而不限制于低于阈值的损失数据的具体分布。Cummins等人研究表明：分布函数的形式和参数对保费率以及其他重要统计量会产生显著的影响，中心数据分布特征会影响到GPD参数的估计。然而，大多数研究成果存在两个缺陷：其一，只考虑尾部特征，而不考虑中心分布，使得风险度量结果可能存在较大误差。其二，GPD建模基础在于阈值u的选择，但是阈值u如何选择，没有统一的方法标准。大多数学者仅仅采取“看”和“取”的主观方法。阈值u需要在超阈值数据稀缺性导致的参数估计不确定性和尾部渐进逼近之间达到平衡，故其精确估计十分困难[95]。常用的阈值选择方法主要是图像诊断法（看）[96]和取高分位数法（取）[97]，这两种方法过于主观，需要大量数据的验证。此外，就算选取了一个合适阈值，由于样本量差异使得无法使用根据似然函数构造的信息准则来判断模型拟合的好坏。如果GPD的形状参数 在（-1，-0.5）之间，参数的极大似然估计不服从常规分布；当小于-0.5时，似然估计则不存在。对此，Behrens和Lopes（2004）[98]，Carreau 和 Bengio（2009）[99]以及Cabras（2011）建立混合模型来克服这些困难。混合模型中，阈值u被视为混合模型中的一个参数，低阈值部分的中心分布视为常规分布，高阈值的数据分布采用GPD来刻画，分布函数中所有参数均使用Bayes计算来估计。Bayes混合模型有效地回避了建模时的阈值估计问题，改善传统方法中阈值单向影响其他参数估计的缺陷，使得所有参数在估计过程中相互联动，相互制约。

②损失分布的改进。

针对传统的单峰、对称分布的不足，本节采用混合分布来改进。由于混合分布可以是多种形式，在拟合厚尾、多峰、分对称数据时，也能取得较高的精度。根据巨灾风险的特征，本小节主要以常规分布如Gamma分布来拟合风险主体部分，以GPD拟合尾部特征来构建混合模型。

（a）混合分布模型。(www.xing528.com)

假设随机变量X服从一个常规分布和GPD的混合分布，小于阈值u的部分服从某个分布形式已知的分布函数H (x /η)，而超阈值部分则来自GPD。随机变量X的分布函数和密度函数可表示为式（8-31）、式（8-32）：

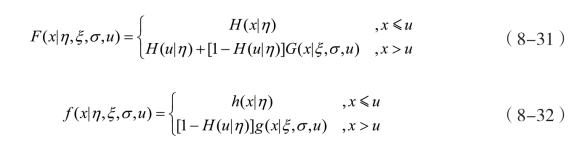
其中，h( x |η)，g (x |ξ ,σ)分别为低阈值部分服从的已知分布和GPD分布的密度函数。不妨令θ1=η ,θ2=(ξ ,σ ),θ =(θ1 ,θ2,u)，由此可得损失样本的似然函数L (θ;X)为：

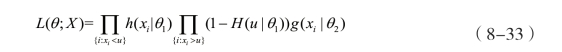
混合模型式（8-31）、式（8-32）和似然函数式（8-33）构造完毕，接下来是参数估计。

（b）Bayes混合分布。

Bayes计算与Bayes推断的基本依据是Bayes公式，其基本思想可以通过式（8-34）表示：

此处，借用Bayes学派的观点和方法，将参数视为随机变量，设置参数先验分布，结合似然函数，通过Bayes计算即可得到参数后验分布。然后，根据后验分布和Bayes决策理论即可得到相对应参数的Bayes估计值。本研究以Gamma分布为低阈值数据分布建立混合分布模型，以平方损失函数作为损失函数，待估参数的Bayes估计值等于其后验分布的均值。

如果灾害损失小于阈值u的部分来自一个Gamma分布总体，超阈值部分来自GPD。在形状参数α和比率参数β均大于0的条件下，Gamma分布的密度函数如式（8-35）所示：

其中，Γ(·)为Gamma函数，其累计分布函数为。因此，（8-35）式可以改写为Gamma-GPD混合分布函数：

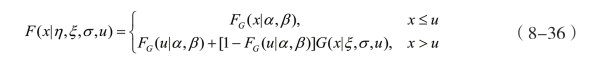
同理，令θ =(α ,β ,ξ ,σ,u)，似然函数可改写为式（8-37）：

假定所有参数相互独立。首先，设α，β的先验分布分别为α～IGamma (a, b)，β～Gamma(c2/d ,c /d )，其中a，b，c，d为超参数。

其次，设定阈值u的先验分布。本文中取正态分布N作为阈值u的先验分布。

再次，GPD参数ξ，σ先验分布的选取。此处根据Jeffrey先验法则，ξ、σ的联合先验分布的选取及后验分布结果分别如式（8-38）、式（8-39）所示。

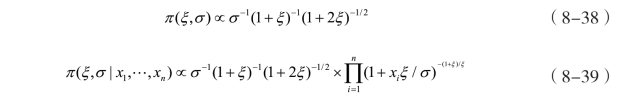
最后，结合上述三个先验分布及似然函数，可以导出参数向量θ的后验分布：

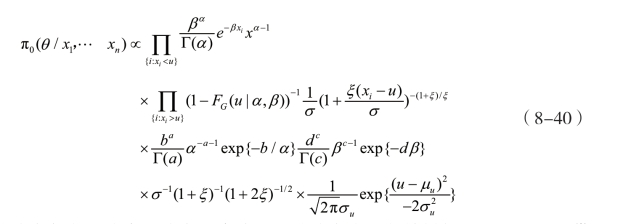
由于该后验分布复杂且非常规分布，直接从后验分布中进行抽样较困难。因此，借助MCMC（Markov Chain Monte Carol ，MCMC）方法进行计算。当所抽取的参数链达到稳态时，该链的极限分布收敛于参数后验分布，所抽取的参数链近似为参数抽样，在平方损失函数下，抽样链的均值即为参数的Bayes估计值。

③聚合损失分布。

（a）灾害发生次数分布。

本文假设灾害发生次数服从Poisson分布。

定义8.1：假设一个随机过程{N (t ),t＞0}表示到t时刻事件发生的总次数，如果它满足以下四个条件：①N (t)≥0；② N (t)的取值为正整数；③∀0 ＜s ＜t ，有N (s )≤N(t )；④∀0＜s ＜t ,N (t )-N (s)表示事件在(s ,t]中发生的次数；那么随机过程{N (t ),t＞0}是一个计数过程。如果事件在两个时间区间不相交时发生的次数相互独立，那么{N (t ),t＞0}是一个独立增量过程。

定义8.2：如果计数过程{N (t ),t＞0}满足：A.N(0)=0；B.N (t)是一个独立增量过程；C.在任何(s ,s +t]的时间区间内，事件发生的次数服从强度为λt的Poisson分布，即∀0 ＜s ＜t ，

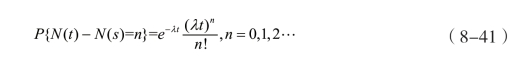
则称{N (t ),t＞0}为具有强度为λ的Poisson过程。

如果将时间间隔确定为单位时间，则，发生次数的均值、方差均为λ，矩母函数为。假设单位时间为一年，那么一年内灾害发生的次数服从Poisson分布。

( b）风险损失聚合。

风险损失聚合是指单位时间内，所有发生灾害造成的总损失，它与灾害发生的次数以及单次灾害发生的总损失有关，索赔次数（灾害发生次数）反映了灾害发生的可能性大小，损失额则刻画了风险损失程度。假设单位时间内的风险损失聚合，Xi表示单位时间内发生的N次灾害中，第i次的损失额N服从参数为λ的Poisson分布。假设每场灾害间的损失相互独立，且发生次数与损失NS有以下特征：

A.假设灾害损失iX是独立同分布于()F·，根据卷积公式，NS的概率分布如下所示：

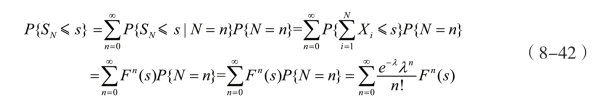
其中，Fn(·)表示()F·的n重卷积。

B.E (SN)=E (X )E (N)=λE (X)。

C.D (SN)=E2(X )D (N )+E (N )D (X)=λ[E2(X )+D (X )]。

D.S的矩母函数M (t )=M[ln(M (t))]=eλ[MX(t)-1]。

N

s N X

如果Xi形式比较简单且属于常规分布，根据特征函数的逆转公式和再生性定理可以推导出SN的分布函数。但是，如果Xi具有一个形式比较复杂的概率分布，如上文中提到的混合分布，那么上述方法将不可行，但是可以运用数值算法和Monte Carlo 算法模拟出NS的分布。SN分布的Monte Carlo 模拟过程如下所示：

Step1：给定Poisson分布参数λ、混合分布参数θ =(α ,β ,ξ ,σ,u)以及需要模拟的随机数个数m；

Step2：从Poisson分布p(λ)中产生一个随机数n；

Step3：从均匀分布U(0,1)中产生n个随机数y1 ,y2…yn ，若0≤yi≤FG (u |α ,β)从截尾Gamma(α ,β)[0,u]分布中产生对应的随机数 xi(0＜xi ＜u)；否则，则从GPD (u ,ξ ,σ)中产生与之对应的xi(xi ＞u)，将x1 ,x2 …xn 累加，即为一个SN的模拟值S；

Step4：重复step2和step3 m次，得到m个SN的随机数S1 ,S2…Sm ；

Step5：画随机数S1 ,S2…Sm 的条形图，运用非参数方法进行拟合优度检验（如K-S、A-D检验等），选择最优拟合分布作为损失聚合SN的分布。

（3）巨灾债券定价模型的构建

鉴于金融定价模型和损失定价模型的缺陷，本段借鉴金融BDT模型同时结合Bayes混合分布模型对巨灾债券进行定价分析。

①利率期限模型。

利率变动是债券定价时必须考虑的因素之一。尽管巨灾债券是具有保险特征的特殊债券，但利率对其定价的敏感性和大多数与利率挂钩的金融产品一样，敏感程度较大。无套利的利率期限结构模型是随机利率分析和金融衍生工具定价最常用的方法之一。尤其是BDT模型，它因结构比较简单、可操作性强，被广泛运用。本处参考Louberge（1999）、李永和刘鹃（2012）[101]提到的方法，结合BDT利率模型的思想，建立离散形式的BDT利率期限结构模型。

模型的基本假定：

A.短期利率变动服从对数正态分布。

B.在一个较短的时间跨度内，利率变动1次且结果只有两种，以p的概率上升到ra和以1-p的概率下降到rb。

C.本期利率波动率与上一期利率波动的方差相等。

D.假设债券每期期末以当期定期存款收益利率Ri支付一次利息，债券到期时支付本金和利息。

债券的本金为单位1，我们以二叉树的形式来刻画随机利率每期期末的状态，如图 8-4所示。利率服从对数正态分布，在每期期末只有两种变化结果ra和rb，且。根据刘鹃和李永（2009）[102]、李永（2010）[103]的推导，式（8-43）的利率结构递推关系成立。

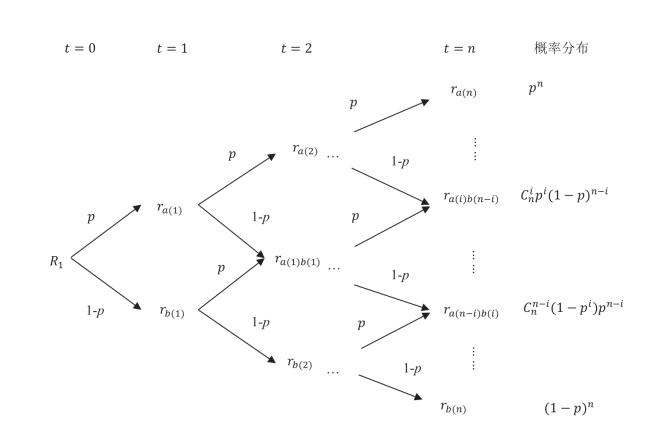
图8-4　利率期限结构BDT二叉树模型

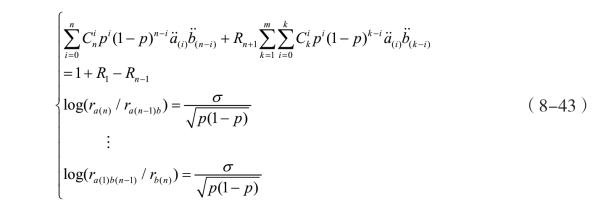
其中，表示贴现因子集合，比如n=3时：

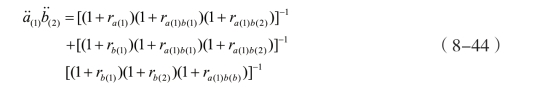
②巨灾债券定价模型构建。

巨灾债券定价的核心在于很好地模拟利率波动过程、巨灾风险和设置触发机制以及赔付规则。本文参考刘鹃和李永（2009）、李永和刘鹃（2010）的方法，尝试构建一个巨灾债券定价模型。一方面，引入BDT二叉树模型模拟利率波动过程，另一方面将Bayes混合分布和Monte Carlo模拟运用到巨灾风险的模拟当中，同时设置不同层级的触发水平和与之对应的赔付函数用来体现触发机制和赔付水平。

（a）触发机制与息票偿付机制。

假定所发行的巨灾债券是在每期期末付息，到期日还本且付最后一次利息的附息债券。息票的支付额度依赖于灾害损失是否达到触发水平。如果损失超过了触发机制的标准，将扣减部分甚至全部的利息，但是会保证本金的按时偿还。假设债券存续期为T期，对于存续期内的任意一期t∈[0,T]期末支付现金流V (t)，假设灾害损失未超过触发水平K时，每期期末支付息票Fr。一旦损失超过触发水平K，息票将会被以(1-q)的比例扣减为qFr，若债券到期时，损失未达到触发水平，则偿还本金和当期风险报酬。具体结构如式（8-45）所示。

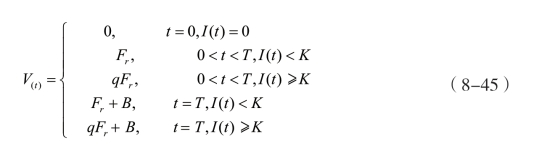
假设触发水平有不同的层级，且与之对应的扣减系数如下表所示，其中K1＜K2＜…＜Km+1，1＞q1＞q2＞…＞qm+1≥0。

表8-1　巨灾债券触发水平和扣减系数设置

（b）巨灾债券回报率和期限结构。

对于利率波动的假设，我们假设其服从如图 8-4所示的BDT二叉树模型结构。到期收益由无风险报酬和定额息票Fr组成。其中无风险报酬率为基本保证收益率，取决于定期存款利率或者国债利率，息票利率为浮动利率。

（c）巨灾风险模型。

假设单次灾害损失概率分布如式（8-41）所示，由一个常规分布和GPD混合而成。假设灾害发生次数是式（8-41）所示的随机过程，单位时间内灾害发生次数服从Poisson分布。由于损失分布比较复杂且不是常规分布，依赖卷积公式、特征函数、逆转公式难以计算SN的分布，故采用Monte Carlo 算法模拟和非参数检验得出SN的分布。

（d）巨灾债券定价。

在上述假定的触发机制和扣减比例下，期末时，息票在各层级触发标准下回收部分的期望值：

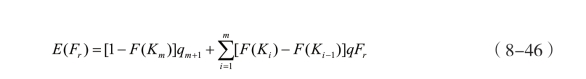
其中(·)F表示损失()I t的分布函数。结合式（8-42）可知：

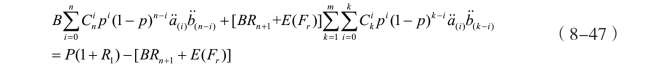
整理后可得式（8-48）：

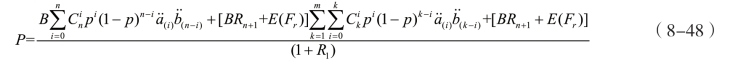
其中，B为保证赔偿金额，E (Fr)为每期期末支付的息票额期望值，R1为一年期无风险收益，Rn+1为n年期无风险收益率，p为短期利率波动的概率，为前向路径贴现因子。

从定价模型中可以看出，巨灾债券的回报率是高于无风险收益率的，其n年期的收益率为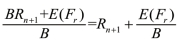，除了无风险收益Rn+1外，还包含了巨灾风险溢价。因此，巨灾债券发行时，因为保证了无风险收益和本金安全，且支付风险溢价，故在相同本金下，巨灾债券收益率高于一般无风险金融债券，支付息票相同的条件下，巨灾债券的发行价格低于一般金融债券的发行价格。