确定评价指标权重，解析西南地区泥石流灾害损失测度与救灾管理

作为AHP法的核心，权重矩阵的构造步骤一般是：①建立一个评价指标系统；②通过两个指标间的比较，确定各自权重的相对重要性，并建立判断矩阵；③用特征值法来确定权数。其中，重要程度的确定由通用规则来确定，如表7-4所示。

表7-4　权重的评分规则

各指标的权数的确定由以下式子决定：

m为判断矩阵中指标的个数，用aij表示xi相对于xj的重要性，表示每行的几何平均数。将各个指标的重要性用一个向量来表示，即为W　，该向量又称为判断矩阵的特征向量。

对判断矩阵进行一致性检验也是一个必不可少的程序。设A为判断矩阵，W为判断断矩阵的特征向量，则判断矩阵的最大特征根为maxλ，且

则一致性指标如下：

最后，判断矩阵的随机一致性比率如下：

其中，RI称为判断矩阵的随机一致性指标，其大小由评价指标的个数的多少来决定，可通过查表获得。通常，R语言的软件包会自带判断矩阵指标参数。(www.xing528.com)

根据前文对重庆泥石流成因的分析，可以建立一级指标的判断矩阵，如表7-5至表7-8所示。

表7-5　一级指标对总指标的判断矩阵

表7-6　二级指标对降水因素的判断矩阵

表7-7　二级指标对物源因素的判断矩阵

表7-8　二级指标对地质因素的判断矩阵

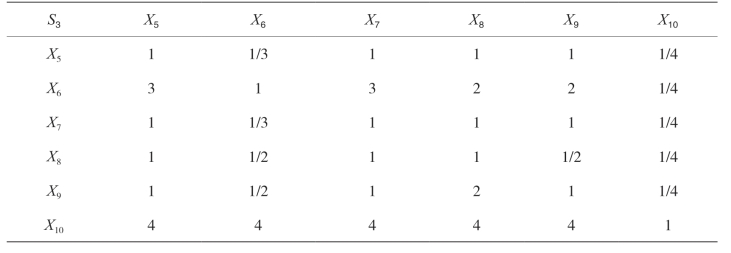
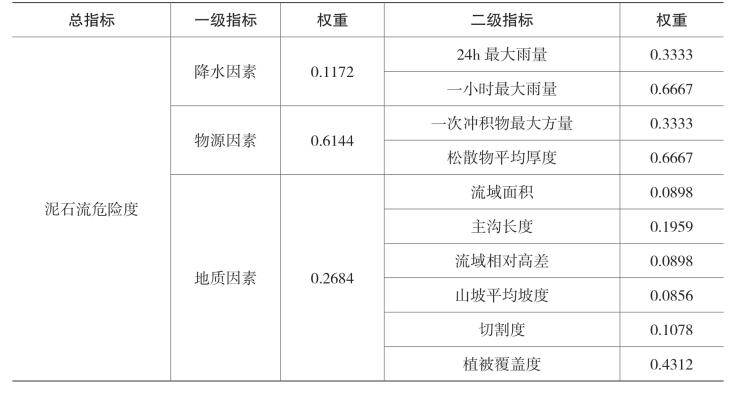
所有矩阵均通过了一致性测试。结果表明，一级指标对总指标的一致性比率约为0.063，二级指标对地质因素的一致性比率约为0.027，均小于0.1。因为当指标数是2时，随机一致性指标为0，默认降水因素和物源因素的一致性测试通过。综上，判断矩阵通过一致性检验，各指标权重如表7-9所示。

表7-9　二级指标对地质因素的判断矩阵