四川泥石流灾害损失及救灾管理

本部分将结合上文中的自然灾害风险测度方法对四川省泥石流灾害的损失风险进行测度。

（1）四川省泥石流灾害损失的统计性描述

对数据的统计性描述有众多方式，本部分主要对四川省泥石流灾害经济损失的集中程度、损失分布进行描述性分析。分析之前，为消除物价水平的影响，需要将历史的损失数据转换为实际损失数据，（5-5）式为实际损失的计算公式。

通过python软件对四川省泥石流灾害损失进行描述性统计分析，其结果如表 5-4和图 5-1—图 5-3所示。在过去29年里，四川省总体泥石流灾害造成的最大实际经济损失为35000万元，最小实际经济损失为0.5万元，平均实际经济损失为2435.332万元，损失分布的偏度为3.616822，峰度为18.73971。四川省第一区域泥石流造成的最大实际经济损失为35000万元，最小实际经济损失为2万元，平均实际经济损失为2863.566万元，损失分布的偏度为3.603471，峰度为17.8258；第二区域泥石流灾害造成的最大实际经济损失为13000万元，最小实际经济损失为0.5万元，平均实际经济损失为824.1333万元，损失分布的偏度为4.425082，峰度为24.81357。根据图 5-1—图 5-3中实际损失的频率直方图与表 5-4所示，四川省总体泥石流损失分布、第一区域泥石流损失分布和第二区域泥石流损失分布都具有右偏性。

表5-4　实际损失的描述性统计

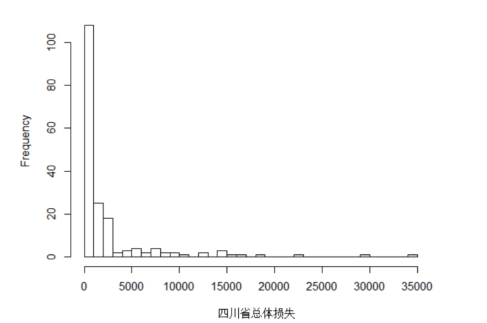
图5-1　四川省总体损失的频率直方图

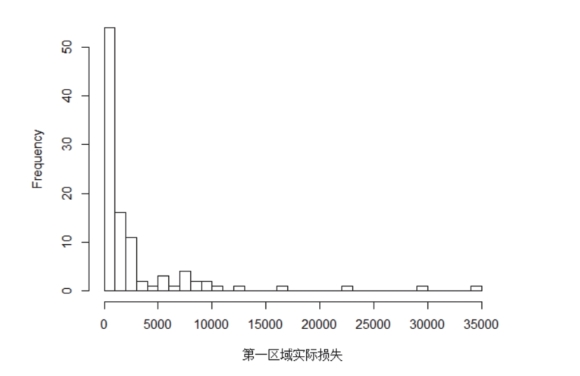
图5-2　四川省第一区域损失的频率直方图

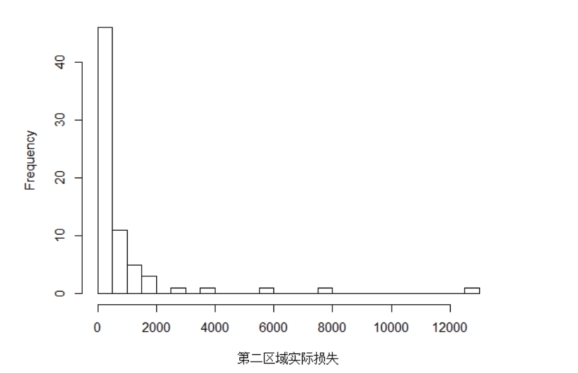
图5-3　四川省第二区域损失的频率直方图

描述性统计分析和损失直方图表明，四川泥石流损失普遍在12000万元以下，少数分布介于12000万元至361000万元之间。其中，第一区域的泥石流损失普遍小于25000万元，少数灾害损失超过25000万元；第二区域的泥石流损失普遍小于9000万元，少数灾害损失超过12000万元，由于损失数据离散度比较高，差异较大，为缩小数据离散差异并更好地对数据信息和分布特征进行提取和描述，对原始损失数据进行对数化处理。对数化处理后的描述性统计量和直方图见表 5-5和图 5-4—图 5-6。表 5-5显示，第一区域泥石流灾害对数损失和第二区域泥石流灾害对数损失的偏度都变为小于0，说明取对数后四川省总体灾害的对数损失、第一区域灾害对数损失和第二区域灾害对数损失的分布变为左偏。因为g-h分布是通过调节正态分布的偏度系数和峰度系数形成的分布，所以本章将用对实际损失取对数后的数据进行拟合。

表5-5　取对数后实际损失的数据特征

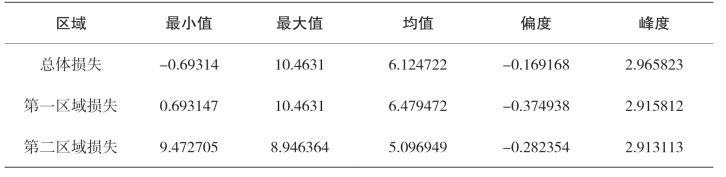
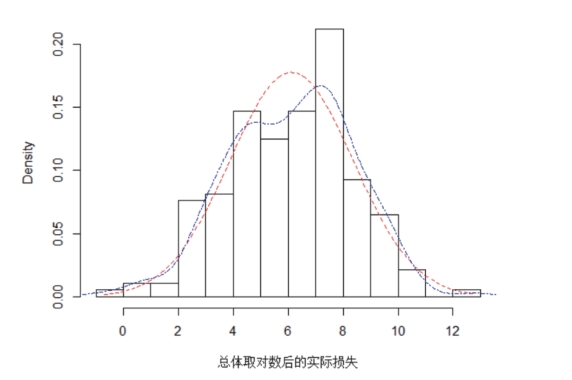
图5-4　四川省总体取对数后的损失频率直方图

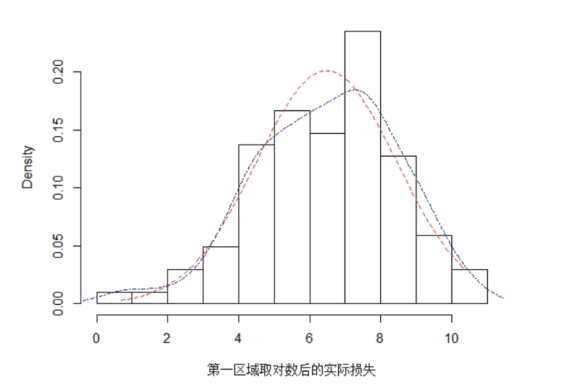
图5-5　四川省第一区域取对数后的损失频率直方图

图5-6　四川省第二区域取对数后的损失频率直方图

（2）四川省泥石流分布的厚尾性检验

四川省泥石流灾害对数损失分布直观上较为接近于正态分布，但仅从描述统计量和直方图上还不足以证明，还需要对三个域的泥石流灾害损失分布是否满足正态分布进行检验。(www.xing528.com)

正态性经验通常用偏度和峰度检验、K-S检验和Q-Q图检验三种方式进行检验。为了更加直观地证明三个区域的泥石流灾害损失的分布接近于正态分布，本章将选取Q-Q图对其进行检验。Q-Q图是通过观察分布的点与对角线的重合程度来判断其分布的相似程度，重合越好，相似度越高，相反则越差。三个区域的QQ图分别见图 5-7—图 5-9。根据Q-Q图显示，在Q-Q图的两端，实际数据和理论数据的差别较大，证明在四川省总体区域和第一区域数据的分位数增长速度与理论正态分布的分位数增长速度相比较，先缓后基本一致，最后又小于理论分位数的增长速度，而在第三区域分位数的增长速度先大于理论分位数，后基本一致，最后小于理论分位数增长速度。进而说明四川省石流的部分损失较大，使得整体的实际损失平均值较大，但我们研究的是四川省泥石流的VaR，根据前文对于VaR的描述，不能把损失较大的数据当作极值点删除，否则将不利于VaR的测度。结合Q-Q图与偏度和峰度的计算，说明四川省三个区域的泥石流的损失分布的确是厚尾型的分布。

图5-7　四川省总体实际损失分布与标准正态分布对比的Q-Q图

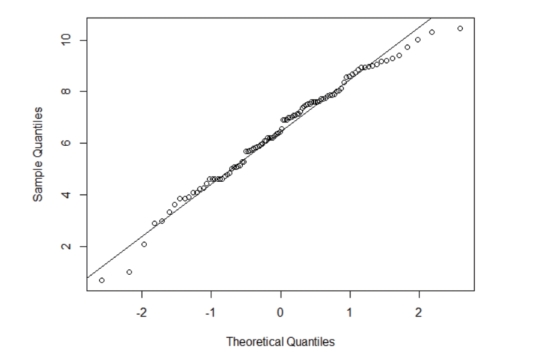
图5-8　四川省第一区域实际损失分布与标准正态分布对比的Q-Q图

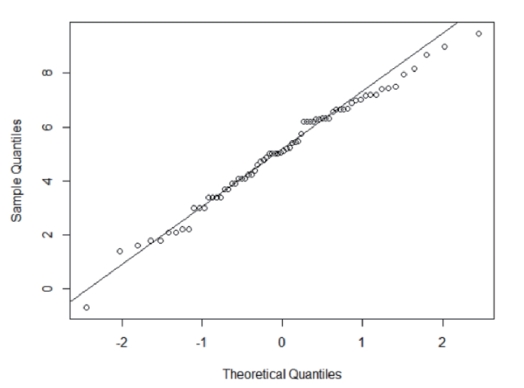
图5-9　四川省第二区域实际损失分布与标准正态分布对比的Q-Q图

（3）四川省泥石流灾害损失的风险测度

① g-h分布与蒙特卡罗结合进行参数估计。

选取拔靴法（Bootstrapping）来计算VaR并对四川省泥石流灾害损失风险测度之前，需要对其历史数据分布进行拟合，由上文可知，四川省三个区域均服从厚尾型分布，且其分布较为接近于正态分布，而对于接近于正态分布的厚尾型数据，说明采用g-h分布对四川省三个部分的泥石流灾害损失数据进行拟合效果较好。为了得到g-h分布的四个参数A、B、g、h的估计，首先，应用蒙特卡罗方法随机模拟10000个标准正态分布数据；其次，应用牛顿迭代法对对称性参数g的初始值进行估计，使得生成新向量yg(z)的偏度与历史数据的偏度接近；然后，再用牛顿迭代法对峰度参数h的初始值进行估计，使得生成新向量yh(z)的峰度与历史数据的峰度接近，把得到的初始值带入（5-10）式和（5-11）式对位置参数A和尺度参数B进行估计；最后，将估计的g、h、A、B值带入（5-3）式，采用梯度下降法对g、h、A、B值进行估计。三个区域的参数估计值如表 5-6所示：

表5-6　g-h分布的参数估计结果

②四川省泥石流对数损失的VaR值估计。

在g-h分布基础上，对四川省不同区域的泥石流对数损失分别在98%、99%、99.5%、99.9%四个置信水平的VaR值进行估计，结果如表 5-7所示。同时，为保证准确性，采用Kupiec的似然比率检验对模型进行检验。似然比率检验法是通过构建LR统计量来对模型进行检验。检验结果见表 5-8。结果显示在四个置信水平下，三个区域的VaR值所对应的LR检验统计量的值均大于5.411894，则表明我们的VaR的估计值通过了检验，即表明所构建模型适用于四川省泥石流损失分布拟合与度量。

表5-7　不同置信水平下取对数后的VaR估计值

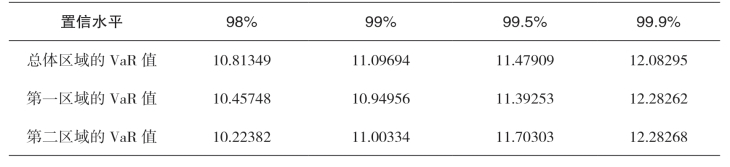
表5-8　不同置信水平下的LR值

本章取置信度为0.01，对应分位点为5.411894，来对模型进行检验。结果显示在四个置信水平下，三个区域的VaR值所对应的LR检验统计量的值均大于5.411894，则表明我们的VaR的估计值通过了检验，检验结果表明用g-h分布与VaR模型相结合可以很好地对四川省泥石流灾害损失进行风险测度。

（4）对四川省泥石流实际损失值的VaR计算

通过对对应的VaR值取e为底的指数值，可以得到在不同置信水平下，四川省不同区域的泥石流实际损失值的VaR值，详细见表 5-9。

表5-9　实际损失的VaR估计值

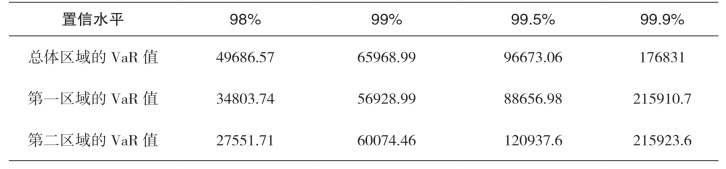
根据表 5-9，在近30年内，在95%、99%、99.5%、99.9%的置信水平下，四川省总体区域的泥石流灾害最大风险损失分别为49686.57万元、65968.99万元、6673.06万元和176831万元；第一区域的泥石流灾害最大风险损失分别为34803.74万元、56928.99万元、88656.98万元和215910.7万元，第二区域的泥石流灾害最大风险损失分别为27551.71万元、60074.46万元、120937.6万元、215923.6万元。