西南地区泥石流灾害风险研究方法研究成果

（1）VaR模型介绍

VaR（Value at Risk，VaR）模型是由JP.Morgan最早提出，并在1995年，世界银行巴塞尔委员会对JP.Morgan提出的VaR模型认可后，VaR风险测度模型迅速推广和应用于金融风险的管理中[9]。VaR又被称为风险价值，被应用于政府机构、保险行业、投资、银行等行业领域的风险度量。VaR描述了在一定时期T内和给定的置水平p下，经济损失在未来可能达到的最大水平。其数学表达式为：

其中，x表示在指定时期T内和置信水平p下可能的损失值。

VaR具有简洁明了、统一风险计量标准、易于理解掌握、可事前计算等优点，但也存在诸多的缺陷和不足，如其原理和统计估计方法上存在一定缺陷，隐含了前提假设以及只能用于正常市场条件下的风险度量。随着VaR模型的逐步成熟，人们通常采用方差协方差法、历史数据法、拔靴法（Bootstrapping）等方法对其进行改进[9]。方差协方差法本质为对风险测定的部分，它在实际应用中需要两个潜在假设：风险资产的价格为线性变化；收益率为正态分布。历史数据法主要利用历史数据的变动序列来对VaR进行计算。拔靴法（Bootstrapping）也是利用历史数据对VaR的值进行计算，但不同于历史数据法，它更侧重于在历史数据的基础上对未来数据进行模拟。三种方法各有优劣，方差协方差法具有容易理解的优势，但具有计算过于复杂、假设条件很难满足的劣势。不需要假设历史数据的分布是历史数据法的优势，劣势也是计算过于复杂，误差较大。拔靴法（Bootstrapping）的优势在于容易理解，计算简便，劣势在于对于历史数据分布的拟合较为困难。为了更加精确地对四川省泥石流灾害损失的风险进行测度，本章将选取拔靴法（Bootstrapping）对其损失风险进行测度。

（2）g-h分布介绍

①g-h分布的定义。

基于正态分布，John Tukey引入不对称性、形状、位置和尺度四个参数从而形成g-h分布，四个参数用字母分别表示为g、h、A和B。根据历史数据调节四个参数的大小，可以使g-h分布较好地对具有厚尾型特点的数据进行拟合。

由g-h分布的定义可知，g-h分布为一个关于z的函数，其中z服从标准正态分布，其数学表达式如（5-2）式所示。

其中g为分布的不对称性参数，把看作yg(z)，h为形状参数，影响分布的峰度，可把看作yh(z)，把yg(z)看作是影响分布的不对称性函数，把yh(z)看作是影响分布峰度的函数。再在（5-2）式的基础上将位置参数A和尺度参数B引入其中，则一个完整的g-h分布如下式所示：

②g-h分布参数估计的方法。(www.xing528.com)

由于g-h分布可以通过合理调节位置参数、尺度参数、对称性参数和峰度参数，将该分布转化为多种分布，如逻辑分布、t分布、均匀分布、指数分布等分布[10-12]，因此可以假设一个g-h分布，通过调节其参数使其分布的特征向量与历史数据的特征向量匹配，从而生成一个与历史数据相符合的g-h分布。本章采用MC算法，随机生成一个标准正态分布，再在此分布的基础上调节A、B、g、h四个参数的值，从而拟合历史数据，使得形成的g-h分布的均值、方差、尺度、峰度与历史数据的均值、方差、尺度、峰度逼近，具体参数估计过程如下：

首先，用MC算法随机产生一组样本量为10000的标准正态分布数据并记为z。

其次，根据历史数据，求得历史数据的均值、方差、尺度、峰度，并将求出来的值分别用m、v、s、k表示。

然后，将g-h分布可以看作两部分，分别将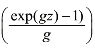看作yg(z)与看作yh(z)。把随机产生的随机向量z分别带入yg(z)和yh(z)，得到yg(z)向量和yh(z)向量，再采用牛顿-拉弗森算法直到yg(z)向量的偏度与历史数据的偏度s逼近，yh(z)向量的峰度与历史数据峰度k逼近。假设yg向量的偏度为s(g)，则估计g的损失函数为f (g)=|s (g )-s |，假设yh(z)向量的峰度为k（h），则估计k的损失函数为y (k)=|k (g )-k |，牛顿迭代方法的收敛阈值为0.0001。

最后，在初步估计了A、B、g、h值后将初始值带入（5-3）式当中，得到新的随机向量y，再通过梯度下降法，使得新的y向量的特征向量逐步逼近于历史数据的m、v、s、k。新估计的A、B、g、h值为g-h的最终估计值。

（3）g-h分布下的VaR值

由前一节所述，本章应用拔靴法（Bootstrapping）对VaR的值进行测度[13-14]。根据g-h分布的分布函数，可知在置信水平为p时，其对应的最大可能损失值为：

根据（5-4）式所示，VaR的值随着p值的增大而增大。