西南地区泥石流灾害风险评估与管理

本节将首先利用云南三江并流区泥石流灾害直接经济损失历史数据，使用巨灾风险研究中的POT（Peaks Over Threshold，POT）模型对直接经济损失数据进行分布拟合，然后结合上一节的泥石流灾害风险预测结果计算各县区的VaR值和ES值，实现泥石流灾害经济损失风险的货币化表示和风险区划。

（1）泥石流灾害单次损失数据描述统计分析

本部分的泥石流灾害直接经济损失数据来源于《云南减灾年鉴》（1991-2017）的灾害损失记录，该年鉴详细记录了云南省各州市历年发生的泥石流灾害时间、地点、人员伤亡情况和财产损失，其中涉及云南三江并流区各县区的记录共75条。由于直接经济损失数据是以灾害发生当年的物价水平计算，在进行损失分布拟合前利用CPI指数进行了调节，将损失数据折算为2017的实际价值，使得折算后的损失数据具有可比性。经过计算，云南三江并流区单次泥石流灾害直接经济损失各描述统计量、直方图和正态P-P图如表 4-16和图 4-5、图 4-6所示。根据结果，单次直接经济损失数额的峰度系数为6.309，表现为尖峰特征，偏度系数大于0代表其损失分布表现为右偏特征，同时其正态P-P图（图 4-6）表现为向右下方凸出表示其损失分布具有厚尾性。由于直接经济损失数据具有的尖峰厚尾性，如使用一般的标准分布进行分布拟合则会造成较大的误差，并且会导致后续的VaR和ES计算出现更大的误差。因此，本章将使用巨灾风险研究中对尖峰厚尾数据具有较好拟合表现的POT模型进行分布拟合。

表4-16　直接经济损失数据描述统计量

（2）基于POT模型的泥石流灾害单次经济损失数据分布拟合

图4-5　直接经济损失数据直方图

图4-6　直接经济损失数据正态P-P图

基于POT模型的泥石流灾害单次经济损失数据分布拟合首先需确定合适的阈值，在确定阈值的基础上估计分布函数的参数值，从而得出损失数据的分布函数。本节的分布拟合使用R软件中的evir程序包完成。

①基于Hill图的阈值选取。

对泥石流灾害单次损失数据进行分析，使用Hill函数绘制出损失数据的Hill图，由此完成对阈值的选取，如图 4-7所示。观察Hill图，图中曲线趋于相对平稳的首个值则为合适的阈值，即阈值u=480。本章将根据该阈值进行POT模型的参数估计和模型检验。

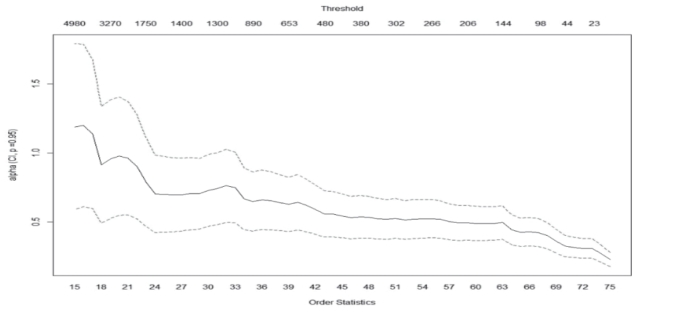
图4-7　直接经济损失数据Hill图

②模型参数估计与诊断检验。

在R软件中带入泥石流灾害单次直接经济损失数据，以u=480为阈值进行参数估计，估计方法为极大似然估计，估计参数和诊断检验图如表 4-17和图 4-8所示。在图 4-8模型检验图 中，（a）图反映的是超出量的分布函数，（b）为残差散点图，（c）为分布函数的尾部概率估计图，（d）为残差Q-Q图。检验图（c）和（d）中的样本点均与图中实线基本重合，说明阈值u=480的选取较合理，具有较好的拟合效果。

表4-17　模型参数估计表(www.xing528.com)

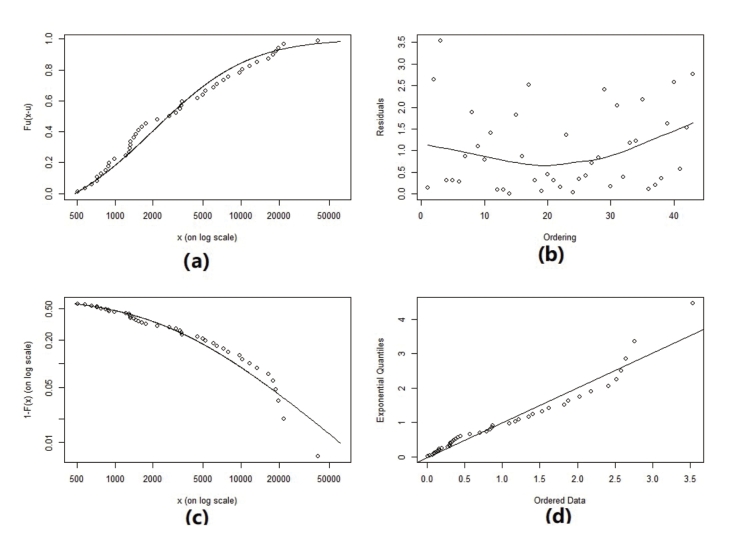
图4-8　模型检验图

根据计算出的树增强型贝叶斯网络（TAN）参数估计结果即可得出云南三江并流区单次泥石流灾害直接经济损失服从的累积分布函数如下：

（3）泥石流灾害经济损失风险计算与风险区划

在对泥石流灾害单次直接经济损失进行分布拟合后，最重要的功能是能利用分布函数计算VaR和ES值完成对泥石流灾害经济损失风险的货币化表示。在以往的灾害风险分析中，计算VaR值最重要的部分在于选取合适置信水平p，结合对应的分布函数计算VaR值，但在计算过程中往往对一个整体地区选择一个置信水平p进行计算，缺乏对区域内各县区具体情况的考虑。本章将以贝叶斯网络模型输出的各县区泥石流灾害发生后验概率值为依据选取各县区对应的置信水平p。结合VaR的定义，泥石流灾害损失发生概率越高的地区，其面临的泥石流灾害风险越大，就需要对应较高的置信水平，计算出的VaR值和ES值则越高。在以往的置信水平选取上，一般依据风险高低按99%、97.5%、95%、90%、85%、80%显示出各县区的后验概率值和风险等级，可用于各县区置信水平的选取，以体现各县区间的风险差异。基于该思想，本章以99%、97.5%、95%、90%、85%、80%的置信水平为基准，构造各县区实际置信水平的计算方式，如表 4-18所示。根据计算得出的各县区对应的置信水平p，计算出的VaR值以及ES值见表 4-18。

表4-18　实际置信水平p计算方式

依据贝叶斯网络测度的泥石流灾害损失发生概率得出了云南三江并流区内各县区的VaR值以及ES值，实现了泥石流灾害损失风险的货币化表示，以大理州巍山县为例，其泥石流灾害损失发生概率较高（达93.07%），则其对应的置信水平也较高（为99.31%），VaR值为80472.82万元，即有99.31%的概率认为泥石流灾害造成的直接经济损失不超过80472.82万元，若超过该值，则直接经济损失的期望值为307986.55万元。

表4-19　VaR与ES计算结果

续表

根据表4-19的计算结果以及按置信水平为99%、97.5%、95%、90%计算的VaR值为边界，按照巨灾风险经济损失分层分担理论得出了云南三江并流区泥石流灾害直接经济损失风险分散表，如表4-20所示。假设研究区均投保了应对泥石流灾害经济损失的保险，则该损失的分散方式为：①在第1层中，主要包括洱源县、宾川县等12个县区，县区数量较多，由于该类县区泥石流灾害发生概率较低，对应的置信水平不高，则由泥石流灾害导致巨额直接经济损失的可能性较低，在实际的灾害风险分散过程中，这类损失可由大型保险公司通过保险产品进行相应的风险分散；②在第2层中，包括了兰坪县和维西县，该类县区存在中等概率的泥石流灾害损失风险，有可能造成巨额直接经济损失，数额可能超过保险公司的赔付能力，超出的部分就需要多家保险公司采取措施共同承担该部分超出的风险；③在第3层中，包括福贡县、弥渡县和剑川县，该类县区面临着高概率的泥石流灾害损失风险，可能造成较大数额的损失，该数额使得大部分保险公司都难以赔付，需针对该部分超出赔付能力的风险实施进一步的再保险以应对该部分超出的风险；④在第4层中，包括华坪县、贡山县、德钦县、泸水县、香格里拉县，县区数量较多，该类县区具有较高概率的泥石流灾害损失风险，其面临的直接经济损失将是巨大的，这就需要利用多种分散手段将超出赔付能力的巨额损失通过如巨灾风险证券化等多种金融手段分散至资本市场才能提升损失应对能力；⑤在第5层中，包括巍山县和玉龙县，该类县区由于面临的泥石流灾害损失风险非常高，其造成的直接经济损失可能会超出多种风险分散手段的赔付能力，需要政府作为最后承担人对超出部分的直接经济损失进行相应的支援与救助才能有效应对。

表4-20　直接经济损失风险分散表