摩擦静力平衡中的哲学思维：教学研究成果

1.课程内容简介

“考虑摩擦的物体平衡问题分析求解”是在“物体系的平面任意力系平衡”学习之后。对于“静摩擦的基本概念”，学生在高中已掌握，但中学分析的力学模型主要是“点”，而理论力学分析对象主要是刚体，因此在平面任意力系的平衡问题分析中考虑摩擦力会增加分析难度，呈现新的特点。学生虽早已了解摩擦角和摩擦自锁概念，却不能应用其对实际问题进行定量分析。故这部分教学内容主要是针对“考虑摩擦的物体系平衡分析”的新特点，即临界状态判定、解的范围分析讨论的分析和讲解。故此部分教学内容主要是：

第一，理解求解呈现的新特点，是静摩擦力在小于等于最大静摩擦力（即0≤Fs≤fsFN）情况下物体都能处于平衡状态所致，求解的关键是掌握临界状态的判定；

第二，建立物理上的临界状态和数学上解的区间的端点值的联系，进而在临界状态下求解后能针对具体问题进行主动力的解的范围的讨论；

第三，能够利用“摩擦角和自锁”概念进行定量分析，即利用“几何法”实现快速便利求解。

2.课程设计思路

第一，课程的引入。首先由工程及生活中的摩擦实例说明“摩擦无处不在，有利有弊”，此处蕴含着辩证唯物主义的认识论。接着由实际问题出发，说明静平衡分析中考虑摩擦力的必要性和新特点，从而引导学生思考：“考虑摩擦的物体系平衡分析”和平面任意力系平衡问题求解有何异同？这里分析求解异同时需遵循求解规律，讲究分析顺序，其中蕴含着《大学》中“物有本末，事有终始，知所先后，则近道矣”的道理。

第二，课程的深入。在由实例演示“考虑摩擦的物体系平衡分析”和平面任意力系平衡问题求解的异同时，详细阐述新特点和分析思路：由于摩擦力不同于其他未知力，其不同的方向对应不同的物理状态，即不同的相对滑动趋势，故在求解前需要分析可能的物理状态，从而给出对应情况下的受力分析图；根据考虑摩擦力列平衡方程和补充方程，并强调说明“临界状态判定”是关键。此处蕴含着“析规律、明方向”的处世哲学。

通过两个典型例题讲解，巩固刚刚总结过的求解新特点及求解思路，并注意引导学生思考“临界状态判定”，明确其真正物理意义及进行临界状态分析的目的和意义；注重临界状态物理意义的讲解，帮助学生建立物理上的临界状态和数学上解的区间的端点值的联系，从数学方程和物理意义两个角度同时分析“解的范围”，既体现了数学方程对物理本质的描述，又反映了物理与数学的统一，由此可延伸出现象与本质的辩证唯物主义的认识论。

第三，课程的升华。由问题引入：如何对摩擦自锁问题进行定量分析，或是对利用摩擦自锁而平衡的结构进行设计？从而对另一种求解方法——几何法（利用摩擦角对静平衡问题进行分析求解）进行讲解。此方法求解的本质是：临界状态下全约束力和法线的夹角是摩擦角，此时每个摩擦点摩擦力和支撑力以全约束力代替，再利用“刚体的三力平衡汇交”建立几何关系，从而快速准确地得到问题的解。此处同样蕴含着“明方向、析规律、知趋势”的处事哲学。

3.具体实施方案

第一，课程内容导入。由工程及生活中的摩擦实例（如图2-12和图2-13所示）说明“摩擦无处不在，有利有弊”。由事物的两面性引出：科技同样是把双刃剑，一方面能够砸烂愚昧和落后，另一方面也可能带给人类无尽的灾难。矛盾推动着社会前进，我们应该正确看待科学技术发展的积极和消极的影响，应具有“正确看待它与社会其他因素的关系，尽可能地发挥科技的正面效应——创造价值、减少损失”的科技价值观。针对摩擦的利弊，想要趋利避害，则需要在对摩擦定性定量分析的基础上掌握规律，从而充分发挥摩擦的积极作用，由此引出教学内容“考虑摩擦的物体系平衡分析”。这里体现了辩证法的两面性：事物对立统一的基本矛盾双方，是构成此事物的根本基础，矛盾双方对立统一、不可分割，没有对立的统一或没有统一的对立都是不存在的；没有矛就没有盾，有矛就必有盾。同时充分反映了马克思主义哲学的辩证思维方式：在我们不知向左拐还是向右拐的时候，哲学并没有为我们指明向哪个方向拐，却全面分析了利弊，以便我们权衡得失。

图2-12　微动摩擦

图2-13　摩擦的利用(www.xing528.com)

第二，课程内容讲解。

授课环节1：以“梯子的摆放”为例帮助学生总结归纳“考虑摩擦的物体平衡问题求解”的新特点（如图2-14）。考虑摩擦力的静平衡问题求解虽然问题的解往往是一个范围，但在求解过程中，为了便于求解，方程往往以等式出现，即在平衡方程基础上列补充方程Fs=fsFN；由于考虑的是临界滑动状态下的最大静摩擦力，所以对临界状态的判定很重要。因此求解过程最关键的一步首先是正确判定临界物理状态，从而明确受力图中摩擦力的方向；然后再根据物理上的临界状态和数学上解的区间的端点值的联系，并结合物理意义和问题具体形式分析，给出问题的解的范围。整个分析求解过程充分体现了“析规律、明方向”的处世哲学。

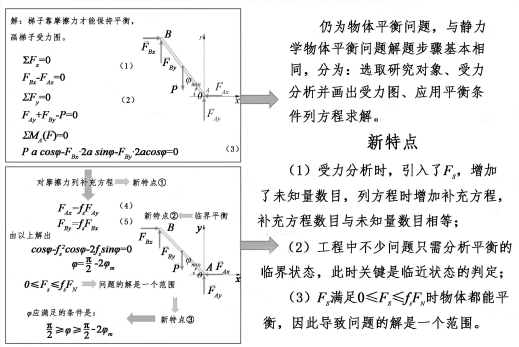
图2-14　梯子摆放问题的求解

为了让学生能够举一反三，这里要通过例题强化教学重难点——临界状态判定和解的讨论。要在反复巩固练习中，引导学生思考“临界状态判定”，明确其真正物理意义；帮助学生建立物理上的临界状态和数学上解的区间的端点值的联系，建立合理的思维方式，即从数学方程和物理意义两个角度同时分析“解的范围”，这里体现了数学方程对物理本质的描述。由此可延伸出本质与现象的辩证唯物主义的认识论：本质与现象是揭示事物内部联系和外部表现相互关系的一对辩证法的基本范畴；本质是事物的内部联系，它决定了事物性质和发展趋向；现象是事物的外部联系，是本质在各方面的外部表现；本质和现象是对立统一关系。通过辩证唯物主义的认识论，帮助学生更深刻地理解求解中“物理与数学的统一”。

授课环节2：首先通过摩擦自锁应用实例（如图2-15）帮助学生简单回顾自锁及摩擦角的概念。接着引用电视节目里的科学小实验（如图2-16），让学生在趣味互动中体会摩擦自锁定量分析和摩擦角的应用。在对该小实验进行解析分析求解以后，引导学生思考：“既然是临界状态下列方程，此时全约束力和法线的夹角是摩擦角，那么能否利用摩擦角从几何直接寻找几何关系求解？”

图2-15　摩擦自锁应用实例

图2-16　摩擦自锁科学小实验

如图2-17所示，摩擦角是临界状态下全约束力和法线的夹角，临界平衡状态下，摩擦力为最大静滑动摩擦力，此时在摩擦点利用全约束力替代摩擦力和法向力，然后根据全约束力与接触法线的夹角为摩擦角，同时刚体满足“三力平衡汇交”，则利用三个力之间的几何关系可以方便快速求解。这种方法称为“几何法”。求解的关键思路为：临界平衡状态下在摩擦点利用全约束力替代→“三力平衡汇交”的判定→利用几何关系求解。此处可延伸“明方向、析规律、知趋势”的逻辑思维，引导学生进行处世哲学思考，提升学生的人文素养。

图2-17　科学小实验的几何法求解

4.教学效果和反思

在进行此部分内容教学时，在对学生的知识特点、思维特点、心理特点进行分析后，考虑到学生之前对相关问题的理解仅仅是定性分析，往往不明确进行定量分析的必要性，且由于认为这是自己已经掌握的知识，并且在实例列举中尤其认为自己已经具备对“摩擦自锁问题”的分析能力，从而产生轻视，更容易产生排斥情绪。因而教学设计中，需注重循序渐进引导思考及知识的趣味性。故本部分整体授课过程的教学策略为：师生互动→问题引入→讲解分析→引导思考→练习巩固→概括总结→延伸思考。然而，在知识目标和能力目标的指引下，尽管注重课堂互动，仍然避免不了例题讲解的枯燥。因此在教学设计中考虑引入育人目标——辩证唯物主义的认识论和马克思主义哲学的辩证思维等的熏陶，以期让学生将看似较为熟知的知识和乏味的解题上升到哲学思维的高度来理解。这不仅能加深学生的理解，而且能起到提升学生的人文素养的作用。对于融入思政元素后的教学效果，通过一个教学问卷调查进行了检验。其中，80%的同学认为这样的授课方式有利于促进他们的理解，较有意思，能够引领他们建立起科学和哲学的联系，起到思维方式训练和价值引领的作用。