高等数学课程思政教学案例实例

根据科学与人文并重、内生与植入相结合的方法，从辩证唯物主义、家国情怀、“三观”教育、科学精神和人文美育等角度挖掘、凝练高等数学课程的思政教学案例。

1.辩证唯物主义

数学蕴含了深刻的哲学思想，结合辩证唯物主义进行高等数学教学，既能挖掘数学的本质，使学生更好地理解数学知识，又能使学生通过具体数学问题领会马克思主义哲学原理，培养学生的思辨能力，形成指导实践的方法论。

案例1：数学危机

在数学历史上曾发生过三次严重的数学危机，每一次危机都在逻辑上冲击着数学的理论基础，使数学陷入矛盾的困境，但每一次危机的化解又是数学的浴火重生，极大地推动了数学的发展。以第二次数学危机——微积分严密化为例，在学生阅读史料的基础上介绍危机的核心是微积分的基础不稳固，而后经过数学家们不懈的努力和研究最终建立起分析基础的逻辑顺序，从而圆满化解了第二次数学危机，推进了微积分理论的系统化和完整化。三次数学危机都说明了“否定之否定”的发展规律，深刻揭示了事物发展的前进性与曲折性的统一，表明事物的发展不是直线式前进，而是螺旋式上升。通过对数学危机的学习，学生深刻体会到“基础不牢，地动山摇”，加深了对微积分知识体系构建的理解，同时体会到人的认识都有局限性和相对性，在学习过程中应该勇于发现新问题，促进旧理论的完善和发展。

案例2：定积分的概念

“定积分”是高等数学的核心概念，也是学生进入积分学的基础。由曲边梯形的面积和变速直线运动的路程两个经典问题导入，抛开背景，抽象本质——“分割、近似、求和、取极限”，蕴含了积分学最深刻的“化整为零，积零为整”的思想。通过直观生动的问题，帮助学生理解唯物辩证法的质量互变规律，“分割近似”是质变前的量变准备，而这一量变过程超过一定限度必然会引起质变，这一限度则是通过求极限的方法来完成。定积分的思想也契合“不积跬步，无以至千里；不积细流，无以成江河”“聚沙成塔，集腋成裘”以及“九层之台，起于垒土”等经典谚语，在单调、抽象的概念讲解中润物无声地将数学、哲学、文学三者有机结合，加强学科之间的联系，弘扬中国优秀传统文化，使教学内容更具广度和深度，增强课程的吸引力。

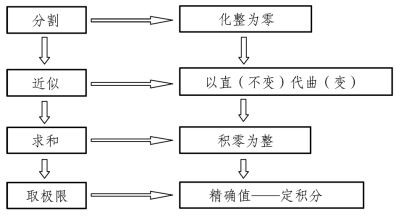
图2-1　定积分的主要思想

案例3：以直代曲

“以直代曲”是微积分学的另一主要思想，蕴含了对立统一的唯物辩证观。从割圆术中正多边形对圆周的逼近，到微分中非线性函数的局部线性化，再到定积分中矩形对曲边梯形的代替，二重积分中平面对曲面的近似，无一不是这一思想的生动体现。通过这些内容的学习，向学生揭示“直”和“曲”的对立性：它们是矛盾的两方面，但又相互转化，通过将“曲”转化为“直”来推动事物的变化发展，最终解决问题，也是用已知解决未知、用简单处理复杂的化繁为简方法论的应用。而现实生活中也不乏“以直代曲”的生动案例，如中国古代的赵州桥用“直”的砖铺出了“弯”的拱券，体现了古代劳动人民的精湛技艺；国家大剧院的椭球形外壳由2万多块矩形的钛金属板组成，彰显了建筑与艺术的完美结合。让学生经历从理论到实践的过程，不断加深对哲学的认识和理解。

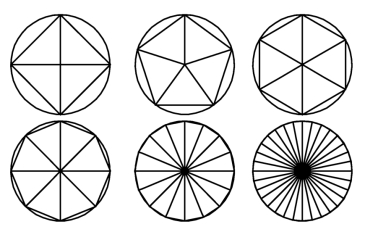
图2-2　割圆术

2.家国情怀

在百年未有之大变局中，帮助学生坚定理想信念，提升国家认同感和民族自信心，增强社会责任感和使命感是课程思政的应有之义。从展示国之强盛，认识国之决策，弘扬国之文化为切入点，融入家国情怀，激发学生树立远大理想，开拓创新，积极进取。

案例1：国之成就

在“重积分应用”部分，针对求解静止轨道卫星所覆盖的地表面积问题，在课程设计中植入实际背景。2020年7月31日开通的北斗三号卫星导航系统是我国自行研制的全球卫星导航系统，对建立畅通、高效、安全、绿色的现代交通运输体系，促进经济社会的发展，保障国家安全等具有重要意义。以此为背景，针对组网卫星中的静止轨道卫星提出问题，让学生带着问题思考学习，在计算论证、解决问题的过程中感受到数学的重要性和实用性，提升民族自豪感和自信心。

又如应用定积分计算坝体填筑量的问题。2012年已投产使用的三峡大坝和正在修建的四川两河口水电站都是世界级的水利水电工程。在完整的水利建筑设施中，大坝坝体设计最为关键，因此坝体的填筑是建设水电站时首先要解决的问题。在开工建设之前需要先计算坝体的填筑量，运用定积分知识来简化计算填筑量问题，更好地服务于工程应用。^[31]这样的设计既能体现国家强盛，又能展示数学的应用价值。

案例2：政治认同

在抗击新冠肺炎疫情中，中国展现出高效的组织领导能力和强大的凝聚力。面对外媒的质疑和批评，如何帮助学生正确评价中国的抗疫模式？这同样可以利用数学理论来进行分析论证。在“微分方程”章节中，介绍传染病SEIR模型^[32]：

该模型符合新冠肺炎疫情的传染特征。将模型进行简化，通过所学知识进行分析求解，对比在采取和不采取严格措施这两种情况下最终的感染人数。利用数据给出科学公正的结论，即事实证明中国的抗疫模式是成功的。

2020年开展的第七次全国人口普查是在中国特色社会主义进入新时代开展的一次重大国情国力调查，对于推动经济高质量发展、完善人口发展战略和政策体系都具有重要意义。借助微分方程的数学模型，从极限理论对人口增长进行估计，验证人口呈指数级增长的结论，即经典的马尔萨斯人口论。进一步阐述工业和现代化带来的老龄化、少子化趋势打破了指数级增长的数学模型，成为全世界所面临的新问题和新挑战。通过学习，引导学生体会利用数学模型研究实际问题的重要意义，理解国家进行人口普查的必要性，同时指出马尔萨斯人口模型具有一定的局限性，激励学生树立应用科学理论来指导和解决国计民生大事的意识。

案例3：文化自信

中国传统文化源远流长，博大精深。从数学中挖掘文化内涵，坚定文化自信。《庄子·天下篇》中的截杖问题——“一尺之棰，日取其半，万世不竭”蕴含了深刻的极限思想。刘徽的割圆术——“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”，首次将极限和无穷小分割引入数学证明，成为人类文明史中不朽的篇章。在计算两个圆柱体直交所围立体的体积和表面积时引入牟合方盖，展现中国古代人民智慧的结晶，让学生认识中国拥有辉煌灿烂的科学探索和理论基础，增强学生的民族自豪感，丰富数学课程的教学内容。

3.“三观”教育(www.xing528.com)

课程思政旨在价值引领，以数学知识和实际生活的紧密联系为抓手，重视人生观、世界观和价值观的正确树立，培养学生脚踏实地、严谨治学的作风和勇于尝试、探索创新的精神，同时注重责任意识、安全意识、环保意识的审视和培养。

案例1：消费意识

在“两个重要极限”章节中采用PBL教学法，植入“校园贷”问题，使学生通过搜集和阅读相关报道，了解“校园贷”中关于复利的计算方式，思考借方偿还金额是否如多数受害学生认为的“很少”。运用该节课程所学知识动手计算还款金额，通过严谨的计算认识到“校园贷”的陷阱及其危害性，积极学习金融和网络安全知识，增强风险意识，远离不良网贷行为。利用和学生息息相关的问题作为案例进行教学，能够引导学生树立理性正确的消费观，自觉抵制享乐主义，形成良好的校园氛围。

案例2：责任意识

在“曲率”教学中利用“3·30永兴火车侧翻事故”引入，加强对工程责任意识的培养。播放视频，分析铁路列车脱轨事故及其原因，了解目前我国铁路采用的铁轨缓和曲线。通过曲率计算公式得出结论，使用三次抛物线可以使曲率连续地由直道曲率过渡到弯道曲率，满足列车行车转弯时的安全需求，有效避免交通事故。从数学的角度论证其合理性，培养学生高度的责任意识和严谨的治学态度。

在“常数项级数”知识点中，利用医学中药物剂量问题导入新课。学生通过查找资料，了解洋地黄毒苷是治疗心力衰竭最常用的强心药物，但有效治疗量、中毒量和致死量相当接近，且药物的耐受性个体差异较大，易发生中毒，因此药物剂量的确定应科学准确。学生利用本节课所学知识进行分析计算，得到结果，认识到在学习和工作中要认真对待每一个微小的细节，不能抱有“差不多”的侥幸心理，避免产生不良后果。同时也让学生体会到医生所担负的重任，对医生这一职业由衷崇敬和尊重。

案例3：环保意识

我国是水资源匮乏型国家，在城市生活用水和工农业用水等方面大力提高水资源的利用率，建立节水型社会是迫在眉睫的问题。在“多元函数微分学的应用”中，提出日常生活中常见的洗衣节水问题，思考应该如何安排每次洗衣淘米的用水量，从而在控制总用水量的前提条件下，使衣服能够洗净。^[33]在学习过程中，学生意识到平时看似唾手可得的哗哗流水其实非常珍贵，认识到暗藏的水资源危机，养成爱护水资源、时刻节约用水的良好习惯，提高环保意识。

4.科学精神

科学精神包括理性精神、实践精神、批判和怀疑精神、创造和探索精神、奉献精神等。数学是科学研究的重要工具和方法，在研究过程中必须尊重科学，发扬科学精神。重视培养学生的科学精神，让科学精神在学习和生活的方方面面指引学生的认知和行为规范，更好地服务于科技发展和社会进步。

案例1：批判精神

数学悖论是指看似无懈可击但逻辑上却导出相互矛盾结果的命题或理论体系，体现了某一发展阶段上数学逻辑基础的局限性。对悖论的大胆质疑和批判促使人们克服这种局限性，从而推动数学的发展。以古希腊哲学家芝诺提出的“阿基里斯与乌龟”的悖论作为问题导入无穷级数的概念，在悖论的认知冲突中深刻理解“有限项之和”与“无限项之和”的区别，引导学生从极限的角度来描述和理解“无限项之和”。通过悖论体会科学的质疑精神和数学家在解决悖论过程中所展现出的求真求实的探索精神。正如数学家J.纽曼所说：“数学中的无穷无尽，其诱人之处在于最棘手的悖论也能够盛开出美丽的理论之花，新的问题会不断地推动科学的发展。”

案例2：蜜蜂精神

蜜蜂是“勤劳”的代名词，代表了团队精神、奉献精神、求实精神和自律精神。蜂巢的构造巧夺天工，它的六角菱形底由三个完全相同的菱形组成，这样的构造使得蜂巢既坚固又节省材料，达尔文曾高度称赞是自然的选择和进化赋予了蜜蜂构造蜂巢的“神力”。在“多元函数的极值”学习中引入蜂巢问题，介绍蜂巢的特殊结构，利用极值的求解方法来验证在相同的容积下蜂巢的构造用料最省。进一步拓展介绍蜂巢的构造在航空航天、材料科学和日常生活中的创新性运用案例，开阔学生的视野，让学生发自内心地认同和学习蜜蜂精神。

案例3：实践精神

积分理论中的“格林公式”沟通了平面区域内部的二重积分和区域边界上的曲线积分，在理论和实践中都有重要价值。测绘学中的面积测量仪的原理就是利用格林公式计算平面有界区域面积。实际使用时只需手持测量仪绕所测区域行走一圈便可进行测量，简便快捷，在农业土地、草场林地、坡地丘陵、工程测绘和地质勘探测量等方面都有广泛应用。通过这一节内容的学习，学生既能深入掌握知识，也能体会科学的实践精神——理论需要实践来检验其真实性，同时也需要将理论应用于实践中，发挥理论的指导作用，增强学以致用的意识。

5.人文美育

数学不仅有着耀眼夺目的真理光辉，具有造福人类的善的功能，也具有独特生动的审美价值和美学意蕴，数学的应用领域已经延伸到了人类社会生活的各个角落。^[34]数学教育不仅追求“真”和“善”，也追求“美”，求美是数学精神和人文精神的融合和升华。课程思政建立了科学与人文融合的新教育价值观。在专业课程中渗透和体现人文教育，引导学生的审美情趣，培养学生的高尚情操，促进学生个性健康发展，形成健全而和谐的人格。

案例1：公式之美

世界最美十大数学公式之一的牛顿-莱布尼兹公式将定积分计算问题转化为不定积分求原函数的相关问题。公式简洁明快，有如电影的倒放功能，使一个看似复杂困难的问题通过思路的转换得以巧妙而简便地解决。^[35]公式深刻揭示了微分和积分之间的联系，沟通了不定积分和定积分，恰似长江大桥“一桥飞架南北，天堑变通途”，充分展示了数学公式的简洁美、和谐美和统一美。在数学教学中渗透人文思想，引导学生欣赏、体验数学的美学意蕴，感受科学和人文的辩证统一。

案例2：音乐之美

通过傅里叶级数分析音乐问题，乐音的声音图形表现出了重复性和周期性，而噪音的图像则是不规则的。在课堂教学中播放乐音和噪音进行对比，根据傅里叶收敛定理推导乐音可以表示为简单的正弦函数之和，而复杂的声音最终都能够表示成简单声音的组合，层层推进，让学生发现理论上看似复杂的贝多芬第九交响曲也完全可以用简单的音叉来进行演奏！^[36]从数学的视角看待音乐，别有一番滋味。

案例3：外形之美

数学在建筑结构和器物的形制方面也有广泛的应用。在学习“旋转曲面”时，由传统工艺中制作陶瓷的七十二道工序之一“拉坯”引入，从数学的角度分析工序的原理，通过视觉化的形象分析陶瓷的形制特点，抽象出旋转曲面的概念。展示并分析国家大剧院外观的几何图形，以及古诗词中“孤舟蓑笠翁，独钓寒江雪”中的蓑笠图形，使学生在形象地掌握数学概念的同时培养个人审美素养，并提升民族自豪感。

教学案例的建设是课程思政挖掘潜在思政元素的重要载体，也是思政教育资源开发的重要环节。秉持以学生为中心、产出为导向、持续改进的理念，深度融合信息技术和教育教学，不断更新教学理念，改革教学方法和创新教学模式，发挥知识传授和价值引领的双核作用，推进课程思政改革建设，努力实现立德树人的根本目标。

（何莎　冯颖）