基于灰色理论的预测方法：研究成果

灰色预测是一种对含有不确定因素的系统进行非线性拟合外推的预测方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度，进行关联分析，并对原始数据进行处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。其用等时距观测到的反应预测对象特征的一系列数量值来构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。其具体的算法如下：

假设一个非负的原始时间数据序列D^（0）有n个观察值z^（0）={z^（0）（1），z^（0）（2），z^（0）（3），…，z^（0）（n-1），z^（0）（n）}，经过一阶累加后生成z^（1）={z^（1）（1），z^（1）（2），z^（1）（3），…，z^（1）（n-1），z^（1）（n）}，其中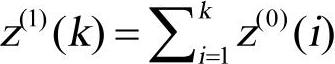，，k=1，2，3，…，n。则一阶单变量的灰色微分方程动态预测模型如下：

式中，α为发展的灰度；μ为内生控制的灰数。

假设待估参数向量θ=（α，μ）^T，可以通过最小二乘法算出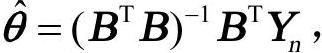其中：(www.xing528.com)

将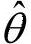的值代入式（9-1）可得

最后可以将预测累加值还原为我们所需的预测值

汽车保有量的历史数据和相关政策的影响等都属于汽车保有量预测的已知信息，这些已知信息属于灰色信息。基于灰色理论弱化信息的随机性，寻找内在的规律性，并利用差分方程和微分方程之间的互换，使用离散的数据序列建立连续的动态微分方程。灰色理论预测法的优点是不需要大量的原始数据来作为支撑，能够将复杂的情况简单化，预测的精度较高。但是由于灰色模型具有快速衰减和递增的属性，并且对历史数据的依赖性较强，如果影响电动车辆数量增长的因素过多、模型灰度较大或者是用于中长期预测时则容易出现较大的偏差，则造成预测结果的精度不佳。