【摘要】:可以看出,由于单排行星齿轮机构有两个自由度,在太阳轮、齿圈和行星齿轮架这三个构件中,任选两个分别作为主动件和从动件,而使另一元件固定不动,或使其运动受到一定的约束,则机构只有一个自由度,整个轮系以一定的传动比传递动力。
从图4-1中可知:
作用于太阳轮上的力矩为 M1=F1r1
作用于齿圈上的力矩为 M2=F2r2
作用于行星架上的力矩为 M3=F3r3
设齿圈与太阳轮的齿数之比为α,则
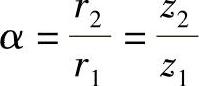
因此 r2=αr1
则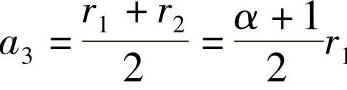
式中 r1——太阳轮的分度圆半径;
r2——齿圈的分度圆半径;
a3——行星齿轮与太阳轮的中心矩;
z1——太阳轮的齿数;
z2——齿圈的齿数。
从行星齿轮的受力平衡条件可得
F1=F2(https://www.xing528.com)
F3=-(F1+F2)
因此,太阳轮、齿圈、行星齿轮架上的力矩分别为

根据能量守恒定律,三个元件上输入和输出的功率的代数和应等于零,即

式中 n1——太阳轮转速;
n2——齿圈转速;
n3——行星齿轮架转速。
将式(4-1)代入式(4-2)得
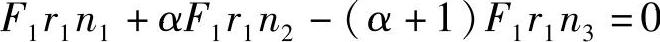
由于F1r1≠0,因此得到
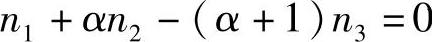
上式即为单排行星齿轮机构一般运动规律的特性方程式。可以看出,由于单排行星齿轮机构有两个自由度,在太阳轮、齿圈和行星齿轮架(行星齿轮与行星齿轮架连成一体)这三个构件中,任选两个分别作为主动件和从动件,而使另一元件固定不动(即使该元件转速为0),或使其运动受到一定的约束(即该元件的转速为某定值),则机构只有一个自由度,整个轮系以一定的传动比传递动力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




