小直径结构物的冲刷应根据其所处的环境条件来进行相适应的分析,可分为水流作用、波浪作用和水流与波浪共同作用等三大类。但对于水流和波浪共同作用的研究很少,下面介绍水流和波浪分别单独作用下的冲刷机理。
1.水流作用
如图8-4所示,当垂直桩柱结构设置在海床上后,水流流态将产生如下变化:①在桩柱结构物前侧和周边产生马蹄涡;②在桩柱结构物后侧产生尾涡,并一般伴随着涡漩发散;③在桩柱的侧面产生流线收缩现象;④由于桩柱迎水侧阻挡使得紧邻区域流速降低而产生下降流。这些现象的综合作用将导致在可冲刷海床条件下土颗粒搬运能力的加强,进而产生了局部冲坑。
水流作用下的冲刷过程主要受到图8-4中马蹄涡和侧面流线收缩的影响,尾涡的影响很小。马蹄涡的形成必须具备两个必要因素,边界层必须具备一定的厚度,且压力梯度差足够大以便形成流线分离。马蹄涡的大小取决于3个基本参量,分别为边界层厚度δ、雷诺数、结构物尺寸与形状。
结构物雷诺数计算为

式中 u——水流剪切流速;
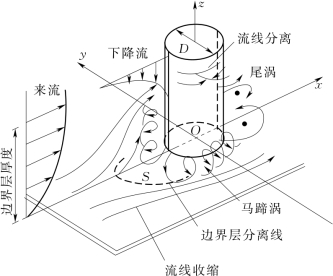
图8-4 桩体存在对水流流线产生的影响[5]
D——结构物杆件直径;
ν——液体运动黏滞系数。
边界层雷诺数计算为

式中 Reδ——边界层雷诺数;
δ——海床剪切边界层厚度。
当边界层厚度与桩径比值δ/D较小时,将使得边界层分离较为困难,进而马蹄涡形成的规模变小。对于更小的δ/D比值,甚至不会出现流线分离,也不会出现马蹄涡。如图8-5所示,其中给出了不同δ/D值对应的马蹄涡水平距离xs(反映马蹄涡的大小)变化趋势,随着δ/D值的增加,马蹄涡水平距离xs逐步增大[3]。
 (https://www.xing528.com)
(https://www.xing528.com)
图8-5 马蹄涡分离距离实测曲线[3]
与δ/D的影响效应相类似,边界层雷诺数Reδ对马蹄涡也有重要影响。当雷诺数Reδ很小时流体处于层流状态,只有当雷诺数Reδ达到一定量值后才可能出现流线分离。图8-5中表格数据点给出了不同雷诺数下对应的马蹄涡水平距离xs值,可见雷诺数Reδ越高,对应的马蹄涡水平距离xs越大。
桩柱结构物的几何形状也影响着马蹄涡的形成。对于流线化的结构物截面形状,如圆柱,其产生的压力梯度较小,故马蹄涡的形成规模也较小;相比而言,对于方桩等具有尖锐角度的结构物,其附近的压力梯度明显要大,故马蹄涡的形成规模也较大。如表8-1所示,圆形结构物马蹄涡的水平距离相对值仅为1.1,方桩可达1.2。
表8-1 结构物形状与马蹄涡相对水平距离[3]

2.波浪作用
波浪作用下的冲刷过程主要受到图8-4中马蹄涡和尾涡的共同影响,因此不仅受到决定马蹄涡大小的3个基本参量(边界层厚度δ、雷诺数和结构物尺寸与形状)的影响,还受到KC常数的影响。KC常数的定义为
![]()
式中 umax——海床面波浪质点最大速度;
T——波浪周期;
D——结构物直径。

图8-6 马蹄涡与波浪相位[3]
当KC常数较小时,波浪质点的运移程度较弱使得冲刷无法有效发展。马蹄涡出现时波浪相位跨度与KC常数实测值如图8-6所示。图8-6中实测数据表明,对于波浪作用而言,只有在常数KC>6的情形下方能出现冲刷。
对于方桩,实测数据表明在常数KC>4的情形下即可产生冲刷,说明在波浪作用下结构物几何截面形状同样影响压力梯度值,这与水流下的影响情况类似。当在波浪影响基础上叠加水流因素后,冲刷产生所需要的KC常数值更低。
由于波浪的周期性,桩柱单侧出现马蹄涡的横跨周期最多为波浪周期的一半,具体横跨周期则取决于KC常数的大小。如图8-6所示,当KC=10时,马蹄涡出现的相位范围在50°~160°;当KC=25时,马蹄涡出现的相位范围在23°~160°。由此可见随着KC常数的增大,单个波浪周期内马蹄涡维持的横跨周期越长,故其冲刷维持效应越久。马蹄涡相对水平距离xs值与KC常数也密切相关,当KC常数较小时,随着KC值增大马蹄涡相对水平距离xs急剧增大,当KC=∞时,则趋近于一恒定值,此时相当于水流作用下的值。
除了马蹄涡的影响外,尾涡也与KC常数密切相关。随着KC常数的不同,尾涡所处的涡旋状态不同。当2.8≤KC<4时,桩柱后侧将成对出现对称分布的涡旋,当进入波浪后半周期时这些涡旋将消失;当4≤KC<6时,涡旋的对称性将消失,但涡旋仍未脱落;当6≤KC<17时,出现涡旋脱落现象,但半个周期内仅有1个涡旋脱落;当17≤KC<23时,仍然出现涡旋脱落现象,但半个周期内有2个涡旋脱落,从而使得桩柱后侧涡旋分布的距离更大,冲刷现象更为严重[3]。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




