整体而言,海上测风塔基础结构设置后引起的海床冲刷一方面源自于结构物附近海床所受剪切应力的增大,另一方面源自于结构物导致水流紊乱状态的加剧[3]。尽管这两种因素同时都会对冲刷产生较大影响,但对第一个方面的研究较多,对第二个方面的研究却较少。当前国际上基本通过第一个方面也即剪切应力的改变来衡量冲刷的程度。
海床泥面处剪切应力的改变通过冲刷应力放大系数来反映,且波浪作用下需要考虑波浪作用的周期性特点。考虑水流作用时放大系数的计算公式为
![]()
式中 τ——结构物设置后的海床剪切应力;
τ∞——结构物设置前的海床剪切应力。
考虑波浪作用时放大系数的计算为
![]()
式中 τmax——结构物设置后波浪周期1为海床剪切应力τ的最大值;
τmax,∞——结构物设置前波浪周期1为海床剪切应力τ∞的最大值。
在稳态流中冲刷放大系数α可达到7~11,图8-2为单桩设置在水流环境中形成的桩周剪切应力的等值线,根据对称性特点图中仅给出了半空间范围的结果。由图8-2可见,一般情况下可近似取放大系数α为11(图8-2中A点)。对于单独的波浪作用下,放大系数α一般要小一些。土颗粒搬运输砂效率q与剪切应力τ的关系为q—τ3/2,由于放大系数α>1,剪应力的非线性增大将导致附近土颗粒搬运冲刷能力增强,从而在结构物附近形成冲坑。这一冲刷过程将持续发展直至结构物附近冲刷放大系数α趋近于1时停止,也即达到冲刷的平衡状态,此时形成最大冲坑深度。
在模型试验中,图8-2中的变量取值为:桩径D=7.5cm,流速V=30cm/s,边界层厚度δ=20cm,δ/D=2.7,雷诺数ReD=2.3×104。(https://www.xing528.com)
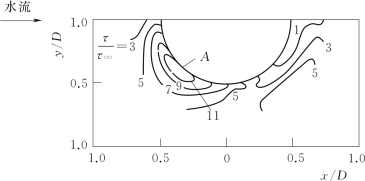
图8-2 单桩结构物周边剪应力放大系数等值线图[3]
冲刷效应的产生是一个渐进的过程,冲刷从开始产生发展到冲刷最大深度(或平衡状态)往往需要一定的时间,而不是瞬时完成的。当已知最终的冲坑深度,为了确定冲坑发展的时长需要进一步确定冲坑发展与时间的关系。图8-3反映的是冲坑发展与时间的关系曲线,该曲线的表达式为

式中 S——平衡状态下最大冲坑深度;
St——t时刻对应的冲坑深度;
T——冲刷的时间尺度。
图8-3中冲刷的时间尺度可根据冲刷与时间的关系曲线而得到,在t=0时刻作曲线的切线(图8-3中虚线)与冲坑平衡深度S所在水平线的交点,该交点距离初始时刻的时间长度即为冲刷的时间尺度。图中的最终冲坑深度和时间尺度是研究冲刷现象的两个主要参数,冲坑深度影响着结构物基础设计和防冲刷措施,时间尺度则影响着冲刷完成的历时。

图8-3 冲坑深度与时间的关系曲线图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




