基础结构节点验算-海上测风塔基础设计

基础结构节点指的是海上测风塔基础结构各组成杆件相互交叉而形成的结构节点，一般多为管形杆件间的节点。基础结构节点不同于基础结构与测风塔塔架之间连接的节点。相比于海上风力发电机组基础结构，海上测风塔基础结构的杆件数量要少得多，因此节点数量也少，且多为简单型式的节点类型。

1.节点类型与构造要求

对于管材，简单节点是主要撑杆（支杆）没有搭接以及没有节点板、隔板或加劲件的节点。按照各撑杆在每一种荷载工况下的荷载作用型式，节点类型可分为K型、Y型（含T型）、X（交叉）型节点，如图7-3所示。对于K型节点，其中一个撑杆的冲剪荷载应由位于节点同一平面内的同一侧的其他撑杆来平衡（若不完全平衡，差值不应超过轴力的10%），如图7-4（a）所示。在T型和Y型节点中，撑杆的冲剪荷载由弦杆的横向剪切力来平衡，如图7-4（b）所示。X型节点中，撑杆中的冲剪荷载通过弦杆传到对侧的撑杆中，如图7-4（c）所示。节点的类型划分并不以节点组成杆件的几何型式来确定，而是根据平面内节点连接处各杆件轴力的分布来划分。对部分由T型、Y型或X型节点承担荷载的撑杆，可根据撑杆轴力在总荷载传递中的份额比例采用内插法来确定，例如，图7-5（a）中节点由50%的K型节点与50%的Y型节点组合，图7-5（b）中节点由50%的K型节点与50%的X型节点组合。

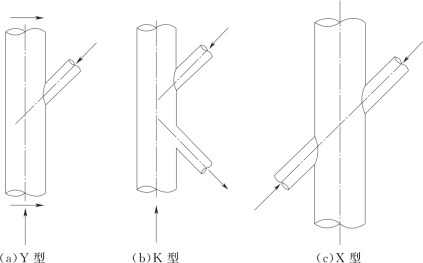
图7-3　基本节点类型

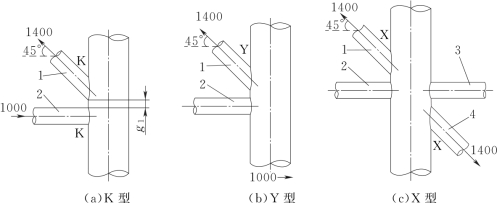
图7-4　节点类型分类示例[15]

1，2，3，4—撑杆编号；1400，1000—撑杆轴力；箭头—力的作用方向；g1—K型节点的撑杆之间的间隙，斜撑杆角度45°

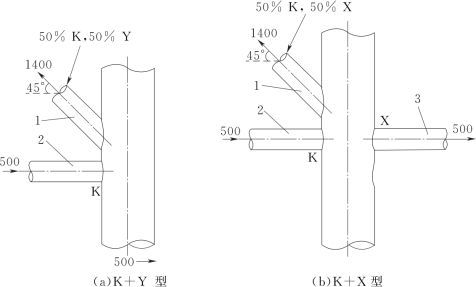
图7-5　节点组合示例[15]

1，2，3—撑杆编号；1400，500—撑杆轴力；箭头—力的作用方向，斜撑杆角度45°

海上测风塔基础的受力相对风力发电机组基础而言要小很多，因此杆件和节点数量少，杆件布置的调整空间较大，一般应避免出现多根撑杆在与弦杆交界处互相搭接，也应尽量避免出现密集节点。节点设计时应满足相关构造设计要求，对于图7-6所示的简单管节点，撑杆不应穿过弦杆管壁，撑杆和弦杆轴线间夹角不宜小于30°。如果在节点处弦杆管壁加厚，则节点加厚管段的长度应超过撑杆外边缘（包括焊脚）以外至少D/4或305mm，取其大者，D为弦杆直径。如果撑杆在节点处增大壁厚或采用特殊钢材，它的长度应从连接端部延伸出最少等于撑杆直径d或610mm，取其大者。理论上的同心节点可用撑杆和弦杆轴线交点作为工作点。工程上不搭接撑杆之间至少有50mm的间隙。为了使弦杆节点所在管段不至过长，沿弦杆轴线上偏心量应不超过D/4[5，16]。

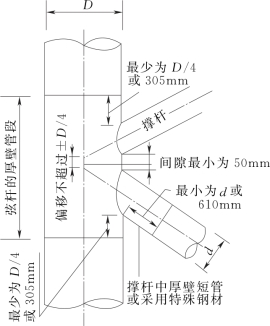
图7-6　简单管节点的构造要求[16]

2.节点强度验算

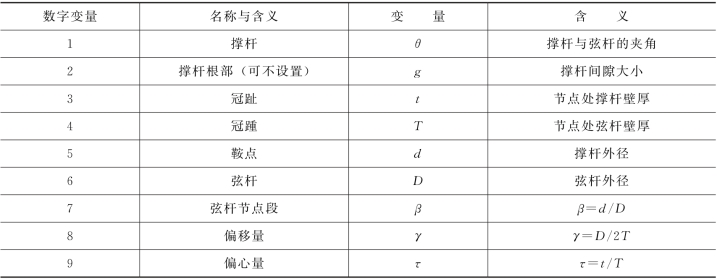
在进行管节点强度验算之前需要定义节点的基本变量，典型管节点的变量定义，如图7-7所示，其中各主要变量的名称与含义如表7-5所示。

节点设计时应保证节点处的撑杆与弦杆强度不低于临近区域各杆件的强度值，节点处焊缝强度应不低于节点总强度，节点强度应不低于各撑杆的结构强度，这一递进强度关系方能确保节点强度满足结构安全工作要求。实际工程中节点处的各变量关系是多变的，一般介于的范围为：0.2≤β≤1.0，10≤γ≤50，30°≤θ≤90°，τ≤1.0。当节点各变量位于上述范围内，且节点处杆件材料的屈服强度fy≤500MPa时，可以按照下面介绍的方法进行节点强度验算。当不满足这些要求时，节点强度的验算可参考相关方法进行。

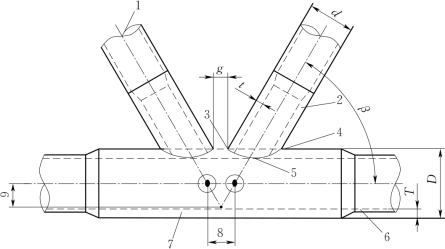
图7-7　典型管节点的变量定义[15]

表7-5　图7-7中各变量的名称与含义

节点强度验算时撑杆和弦杆的轴力与弯矩采用荷载效应基本组合下的设计值。节点处杆件可能存在不同应力水平的轴力和弯矩，它们之间会产生相互影响。对于节点处所有杆件，考虑这一相互影响的节点强度验算方法为

式中 Uj——节点利用水平；

PB——撑杆轴力设计值；

MB——撑杆弯矩设计值；

Pd——节点轴力抗力设计值；

Md——节点抗弯强度设计值；

ipb——平面内弯曲；

opb——平面外弯曲。

为了确保节点处节点屈服后于杆件失效的顺序要求，对基础结构安全与稳定性有重要

影响的杆件节点，除了满足式（7-111）要求外，还应满足以下要求，即

式中 γz——节点附加抗力分项系数，一般情况可取1.17，必要时也可根据杆件重要性程度予以适当降低，但最低不应小于1.0。

节点处轴力和弯矩的抗力设计值分别为

式中 Puj——节点轴力抗力极限值；

Muj——节点弯矩抗力极限值；

γR，j——管节点的抗力分项系数，取1.05。

节点处对于轴力和弯矩的极限抗力值分别计算为

式中 fy——节点处弦杆材料指定的屈服强度，且不应大于0.8倍抗拉强度；

T——弦杆壁厚；

d——撑杆外径；(www.xing528.com)

θ——节点处撑杆与弦杆的夹角；

Qu——强度影响系数；

Qf——弦杆轴力影响系数。

强度影响系数Qu与节点类型和杆件受力模式有关，根据表7-6中计算式来计算。

表7-6　强度影响系数Qu的计算公式[15]

表7-6中参量Qβ为几何影响系数，当撑杆与弦杆外径之比β大于0.6时，其值为

当β≤0.6时，Qβ=1.0。

表7-6中参量Qg为撑杆间隙影响系数，当节点处撑杆间隙g与弦杆壁厚T的比值g/T≥2.0时可计算为（但Qg最小不应小于1.0）

其中

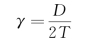
式中 D——弦杆外径。

当多根撑杆在与弦杆节点处互相搭接且g/T≤-2.0时，Qg计算为

式中 φ——计算系数。

当g/T＜0时，表示节点处撑杆相互搭接。当-2＜g/T＜2时，Qg按照式（7-118）和式（7-119）的计算值进行线性内插计算。

式（7-119）中计算系数φ计算为

式中 fy，b——节点处撑杆的屈服强度；

t——撑杆壁厚；

T——弦杆壁厚。

式（7-115）和式（7-116）中弦杆轴力影响系数Qf计算为

式中 λ——与撑杆受力方式有关的系数，当撑杆受轴力作用时取0.030，当撑杆受平面内弯矩作用时取0.045，当撑杆受平面外弯矩作用时取0.021；

qA——弦杆应力水平参量。

式（7-121）中参量qA的计算应采用荷载效应基本组合下弦杆的内力设计值，计算方法为

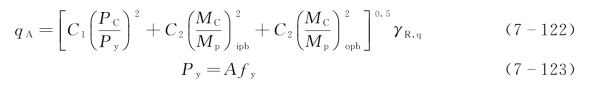
式中 PC——弦杆轴力设计值；

MC——弦杆弯矩设计值；

Py——不考虑屈曲效应下弦杆轴力极限值；

fy——弦杆材料的屈服强度；

A——弦杆截面面积；

Mp——弦杆塑性弯矩值；

γR，q——抗力分项系数，取1.05；

ipb——平面内弯曲；

opb——平面外弯曲；

C1、C2——系数，与节点类型和节点处撑杆受力方式有关，取值如表7-7所示。

表7-7　系数C与C[15]12

按照式（7-122）计算参量qA时，若弦杆节点处两端计算值不同，应取大值代入式（7-121）计算弦杆轴力影响系数Qf。对于K型节点当弦杆轴力为拉力时，在计算Qf时可不考虑轴力作用。

综合节点强度验算方法，节点强度不仅与节点处杆件材料强度和几何变量有关，还与杆件的受力模式相关，进而导致相同的杆件和节点型式与杆件内力不同时，其节点强度各不相同。因此在验算节点强度时，应对节点处各杆件依次进行计算，每一根杆件应分别计算轴力拉伸或压缩、平面内弯曲和平面弯曲作用下的总效应。当节点属于多种节点类型组合型式时（图7-5），应根据每一节点类型所占的比例，将按照式（7-115）和式（7-116）各自计算得到的Puj和Muj按比例累加得到最终的组合值来进行节点强度验算。