海上测风塔基础设计的基础钢结构强度与稳定性

海上测风塔基础结构多由钢管桩或导管架结构所组成，钢管桩和导管架主导管经常设计成内外水压贯通的结构，而不是内心隔水的空腔结构，基础结构在工作状态下内外水压基本平衡，短时间内可能因为水位变化速度较快而存在一定的内外水压不平衡，也即结构会存在较小水头的静水压力作用，但这一短期作用效应对结构强度和稳定性的影响可以忽略。在水面附近连接钢管桩或导管架主导管的撑杆（支管）结构多为隔水的空腔结构，将受到静水压力作用，但水面附近的静水压力通常很小，这一作用仍可以忽略。下面给出的基础钢结构强度与稳定性验算方法均不考虑静水压力作用。

基础钢结构包含四种基本受力构件类型，即轴心受拉构件、轴心受压构件、拉弯构件和压弯构件，不同的构件应进行不同项目的计算与验算。对于轴心受拉构件和拉弯构件应验算强度项，对于轴心受压构件应验算强度、整体稳定性和局部稳定性，对于压弯构件应验算强度、弯矩作用平面内稳定性、弯矩作用平面外稳定性和局部稳定性。

1.强度验算

（1）轴向拉伸与压缩。当构件截面形状为圆形时，轴向受力杆件的轴向应力fn计算为

式中 N——乘以荷载分项系数后的组合荷载拉力或压力设计值；

D——桩外径；

t——桩壁厚。

当构件截面形状不为圆形时，轴向应力fn计算为

式中 An——构件净截面面积。

轴向拉伸杆件或压缩杆件应满足的强度要求为

式中 f——钢材的抗拉或抗压强度设计值。

对于Q235牌号钢材，f=fy/γR=fy/1.087，对于Q345、Q390、Q420牌号钢材，f=fy/γR=fy/1.111，fy为钢材的名义屈服强度，γR为抗力分项系数。

（2）剪切。在主平面内受弯的构件，其抗剪强度应验算为

式中 V——计算截面的剪力设计值；

S——计算剪应力处以上毛截面对中和轴的面积矩；

I——毛截面的惯性矩；

t——壁厚；

fv——钢材的抗剪强度设计值。

根据畸变能屈服准则，当梁腹板中的剪应力达到受剪屈服强度fvy=fy/3时即进入塑性，因此抗剪强度设计值取值为

对于钢管构件（直径为D，壁厚为t），可采用下述过程推导得到其抗剪强度计算式。钢管构件的面积矩计算为

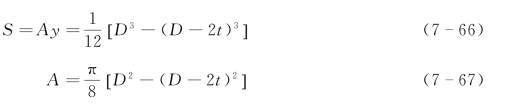
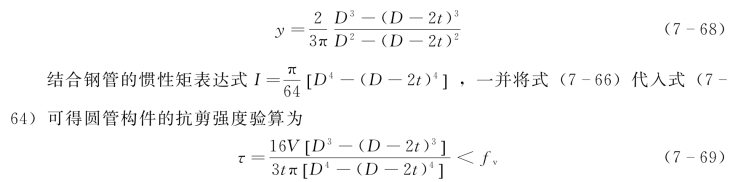
（3）扭转。对于受扭的构件，其扭转剪切强度应计算为

式中 Mp——作用在构件上的扭矩设计值；

Ip——极惯性矩；

D——构件的外径。

钢管构件极惯性矩Ip的计算为

（4）弯曲。在主平面内受弯的构件，其抗弯强度应按以下规定验算，即

式中 Mx、My——同一截面处绕x轴和y轴的弯矩设计值；

Wnx、Wny——对x轴和y轴的净截面模量；

γx、γy——截面塑性发展系数。

对于受弯构件而言，当梁的最外侧纤维刚刚达到钢材的屈服点时，梁处于弹性工作阶段。当作用弯矩继续增加时，塑性逐渐往梁内发展，直至整个截面全部达到塑性，即出现塑性铰为止。截面形状系数γF定义为塑性截面模量Wp与弹性截面模量W的比值。尽管有效利用截面塑性的发展可取得较好的经济性，但考虑到塑性过度发展会使得塑性变形导致梁不适于继续承载。综合考虑后，采用截面塑性发展系数来代替截面形状系数γF，截面塑性发展系数与截面型式、塑性发展深度和截面高度的比值、腹板面积和一个翼缘面积的比值以及应力状态等有关，其介于1.0～γF之间，对于圆管截面，γx=γy=1.15。

（5）拉弯或压弯。在轴心力设计值N和弯矩设计值M的共同作用下，弯矩作用在主平面内的拉弯构件或压弯构件，其强度判别应满足

式中 fn——轴向应力，按式（7-61）或式（7-62）计算。

2.稳定性验算

（1）受压构件的稳定性。受压圆管或圆柱形杆件的稳定性包括整体稳定性和局部稳定性两个方面。整体稳定性验算时应满足(www.xing528.com)

式中 φ——轴心受压构件的稳定性系数，取截面两主轴稳定系数中的较小者，应根据杆件的长细比、钢材屈服强度和截面分类来综合确定。

受压圆管的管壁在弹性范围局部屈曲临界应力理论值很大，但管壁局部屈曲与板件不同，其对钢材的缺陷特别敏感，实际屈曲应力比理论值低很多。无论是轴压构件还是压弯构件，圆管的局部稳定性通过以下截面构造要求来满足，即

式中 D——杆件外径；

t——杆件壁厚。

圆管或圆柱形构件的长细比λ为

式中 l0——杆件的计算长度，取值如表7-1所示；

i——构件截面对主轴的回转半径；

D——直径；

t——壁厚。

表7-1　计算长度l0的确定[11]

注：l为构件的几何长度，即节点中心间距；l1为弦杆侧向支撑点之间的距离。

定义中间变量λn，其表达式为

式中 E——钢材的弹性模量。

整体稳定性系数φ的计算以变量λn为划分标准，分段计算为

（2）受弯构件的稳定性。在最大刚度主平面内受弯的构件，其整体稳定性应验算为

表7-2　a1、a2、a3的取值[11]

式中 Mx——绕强轴作用的最大弯矩设计值；

Wx——按受压纤维确定的梁毛截面模量；

φb——梁的整体稳定性系数。

式中 λy——梁在侧向支撑点间对截面弱轴y—y的长细比。

当采用式（7-82）的计算值大于1.0时应取φb=1.0。

（3）轴力和弯曲联合作用的稳定性。轴力和弯曲联合作用下，在弯矩作用平面内其稳定性判定为

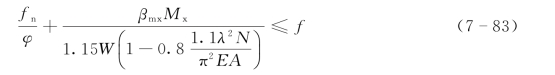
式中 βmx——弯矩作用平面内的等效弯矩系数，使构件同向曲率时（无反弯点）βmx=1.0，使构件产生反向曲率时（有反弯点）βmx=0.85；

Mx——最大弯矩设计值；

N——组合荷载压力设计值；

E——钢材弹性模量；

A——截面面积；

W——弯矩作用平面内对较大受压纤维的毛截面模量；

φ——弯矩作用平面内的轴心受压杆件稳定系数。

轴力和弯曲联合作用下，在弯矩作用平面外其稳定性判定为

式中 βtx——弯矩作用平面外的等效弯矩系数，可类比βmx的取值方法；

η——截面影响系数，闭口截面取0.7，其他截面取1.0；

φ——弯矩作用平面外的轴心受压构件稳定系数；

φb——均匀弯曲的受弯构件整体稳定系数。