m法计算简图及无量纲系数表

将土体视为弹性变形介质，其水平抗力系数随深度线性增加，地面处为零。对于低承台桩基，在计算桩基时，假定桩顶标高处的水平抗力系数为零并随深度增长。m法假设土的水平地基抗力系数随深度呈线性增加，即

式中 k——土的水平地基抗力系数，k N/m3；

m——土的水平地基抗力系数随深度增长的比例系数，k N/m4；

z——计算点深度，m。

一般情况下，m值宜通过单桩水平静载试验确定。由于影响水平受荷桩受力与变形特性的仅为有限深度范围内的土层，而地基土一般为成层分布，因此通常近似采用厚度加权平均值来计算。

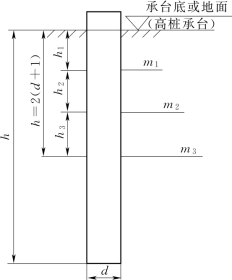
图6-10　m法计算简图[1]

当桩侧面由几种土层组成时，应求得主要影响深度hm=2（d+1）（单位为m）范围内土层的m值作为计算值，其中d为桩径，如图6-10所示。

当hm深度内存在两层不同土时，m值计算为

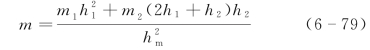
式中 m1——第一层土的m值；

h1——第一层土的厚度；

m2——第二层土的m值；

h2——第二层土的厚度。

当hm深度内存在3层不同土时，m值计算为

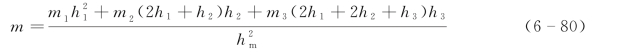
式中 m3——第三层土的m值；

h3——第三层土的厚度。

当hm深度内存在四层不同土时，m值计算为

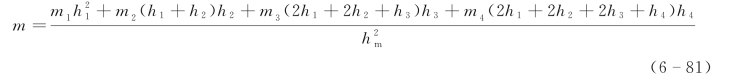
式中 m4——第四层土的m值；

h4——第四层土的厚度。

当hm深度内存在更多层土时，可以按照上述计算规则类推得到。

桩侧单位面积极限水平土抗力标准值可计算为

式中 p——泥面以下深度z处作用于桩上的水平土抗力标准值，k N/m；

y——泥面以下深度z处桩的侧向水平变形，m；

b0——计算桩径，m，其确定方法参见式（6-26）和式（6-27）；

k——土的水平地基抗力系数，k N/m3，按式（6-78）计算。

对于m法，一般采用基于弹性地基梁的有限单元法或有限差分数值法可方便地得到桩身位移和内力分布，而且结果更为准确。也可以根据相关图表和公式计算水平荷载下桩身的水平位移和桩身内力，以及最大弯矩和最大弯矩的分布位置，此时应首先根据式（6-79）～式（6-81）进行主要影响深度范围内各层土m值的换算。(www.xing528.com)

在水平力和力矩作用下，弹性长桩的桩身变形和弯矩的确定，应根据桩顶约束情况来分别计算。当桩顶可自由转动时，桩身入土段的变形和弯矩计算[2]为

式中 Y——桩身在泥面以下的变形，m；

M——桩身弯矩，k N·m；

H0——作用在泥面处的水平荷载，k N；

M0——作用在泥面处的弯矩，k N·m；

T——桩的相对刚度特征值，m；

EP——桩材料的弹性模量，k N/m2；

IP——桩截面惯性矩，m4；

Ay、By、Am、Bm——计算变形和弯矩的无量纲系数，按表6-19确定；

m——桩侧地基土的水平抗力系数随深度增长的比例系数，k N/m4，地基土成层时m采用地面以下1.8T深度范围内各层土m值的加权平均值；

b0——桩的换算宽度，m。

表6-19　m法计算时无量纲系数表[2]

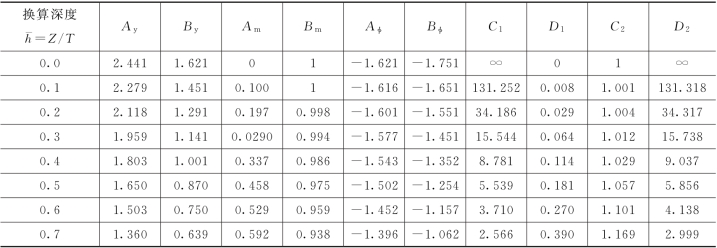
续表

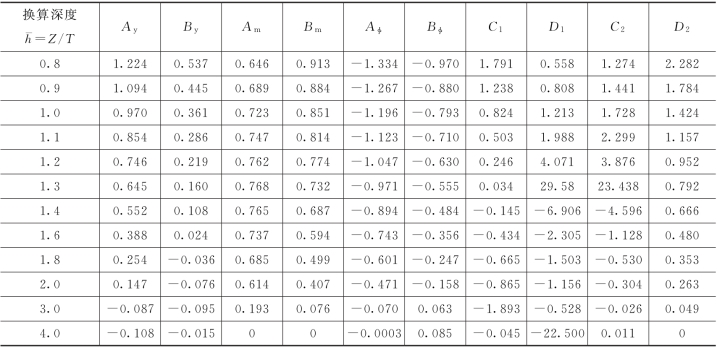
注：本表适用于桩端置于非岩石土中或支立于岩石面上的弹性长桩。

水平受荷桩桩身最大弯矩和对应的位置计算为

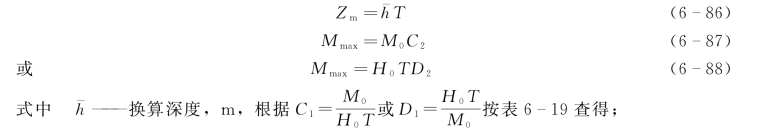
Mmax——桩身最大弯矩，k N·m；

C2、D2——无量纲系数，根据h-=Zm/T按表6-19查得。

当桩顶水平移动自由而转角固定时，桩身入土段的变形和弯矩计算为

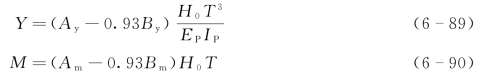
式中 Y——桩身在泥面以下的变形，m；

M——桩身弯矩，k N·m；

H0——作用在泥面处的水平荷载，k N；

T——桩的相对刚度特征值，m；

EP——桩材料的弹性模量，k N/m2；

IP——桩截面惯性矩，m4；

Ay、By、Am、Bm——计算变形和弯矩的无量纲系数，按表6-19确定。