纵观桩基工程的发展,常用的单桩沉降分析方法主要包括弹性理论法、荷载传递法、剪切位移法、分层总和法以及其他数值分析方法等,每种方法都有各自的优缺点。
弹性理论方法由Poulos率先提出[5],将土体看作均质的、连续的、各向同性的弹性半空间体来分析,土体性质不因桩体的存在而变化,多采用Mindlin基本解(应力解答和位移解答)[6],并能合理反映土体的连续性或相互作用,比较容易拓展到群桩分析中。实际中地基土多为层状分布,但土层分层对应力分布的影响并不大,因此弹性理论方法在工程上仍然可以适用,但仅是一种近似分析方法。如果从更准确分析目的出发,也可以通过传递矩阵方法并利用Hankel变换,根据多层弹性半空间轴对称问题的解析解来对层状土体进行弹性理论法分析[7]。当采用弹性理论方法计算时,在单桩分析基础上可以引入相互作用系数的概念从而方便地实现群桩沉降分析。
荷载传递方法将桩与土体的作用简化为一系列竖向分布的弹簧,弹簧刚度多为非线性以反映土体的特性,但不同位置处桩土作用并不互相影响,也即采用了非连续介质假定。荷载传递法的关键在于建立一种真实反映桩土界面侧摩阻力和剪切位移的传递函数。传递函数的建立一般有两种途径:一是通过现场测量拟合;二是根据一定的经验及机理分析,探求具有广泛适用性的理论传递函数。目前主要应用后者来确定荷载传递函数。该方法的优点是能较好地反映桩土非线性作用和地基土的分层特性,计算简便。由于其不考虑桩身各点以及外部点的相互作用,因此难以直接应用于群桩中。该方法后期的拓展也可以反映相互作用的影响,此时多将最初的荷载传递法称为传统荷载传递法。拓展方法比较有代表性的诸如,O'Neil在单桩的荷载传递方法基础上,结合点对点的Mindlin基本解实现了群桩分析[8],不足的是该方法需要迭代计算;Chow在此基础上,基于Randolph单桩分析理论[9]的理论荷载传递曲线[10],摒弃了传统的经验荷载传递曲线形式[11-12],提出了土体切向剪切模量的概念,实现了不用迭代计算的桩基础分析方法[13]。
剪切位移法是假定荷载作用下桩身周围土体以剪切变形为主,桩土之间没有相对位移,将桩土视为理想的同心圆柱体,剪应力传递引起周围土体沉降,由此得到桩土体系的受力和变形的一种方法。Cooke通过在摩擦桩周用水平测斜计量测桩周土体的竖向位移,发现在一定的半径范围内土体的竖向位移分布呈漏斗状的曲线[14]。当桩顶荷载小于30%极限荷载时,大部分桩侧摩阻力由桩周土以剪应力沿径向向外传递,传到桩尖的力很小,桩尖以下土的固结变形是很小的,故桩端沉降不大。据此认为评定单独摩擦桩的沉降时,可以假设沉降只与桩侧土的剪切变形有关。Rondolph进一步发展了该方法,使之可以考虑可压缩性桩,并且可以考虑桩长范围内轴向位移和荷载分布情况,并将单桩解析解推广至群桩[9]。Kraft考虑了土体的非线性性状,将Rondolph的单桩解推广至土体非线性情况[10],Chow将Kraft的解推广至群桩分析[15]。(https://www.xing528.com)
分层总和法也称为单向压缩分层总和法,仅考虑桩侧摩阻力和桩端应力引起的桩端有限厚度范围内土体的压缩变形,当桩布置较为稀疏时还应包含桩身范围内桩身压缩量。该方法仍然以半无限空间均质土的弹性理论解答为基础,可考虑群桩之间或周边荷载的相互作用影响,是一种容易理解也实施简便的分析方法,在我国桩基工程领域有着广泛的应用,在此基础上引入经验系数修正后的沉降计算结果往往有着较高的准确性。
在工程领域广泛应用的方法有分层总和法和传统的荷载传递法。前者在我国应用较为广泛,后者在欧美国家的工程领域应用较多。
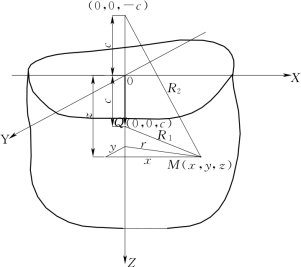
图6-2 竖向荷载作用下Mindlin解答分析图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




