海上测风塔基础设计：波浪荷载计算方法

对于海上测风塔的基础型式，测风塔底端的平台无非是钢平台或钢筋混凝土平台，因此为了保障测风塔的正常工作，平台高程需位于波浪最高点以上并留有一定的安全裕度。测风塔的荷载量级决定了其基础结构的杆件数量较少，且杆件的截面尺寸相比海上风力发电机组基础结构而言要小得多，杆件直径D与波浪波长L之比远小于0.15，因此测风塔基础结构波浪荷载计算可采用莫里森（Morison）方程。

1.莫里森（Morison）方程

Morison方程是一种半经验半理论计算公式，该理论假定，柱体的存在对波浪运动无显著影响，流场中各点的速度和加速度仍可按第4章中相关波浪理论来确定。同时认为波浪对柱体的作用主要是黏滞效应和附加质量效应。设有一柱体，直立在水深为d的海底上，波高为H的入射波沿x正向传播，柱体竖向中心轴与海底线的交点为坐标系（x，z）的原点，如图5-2所示。

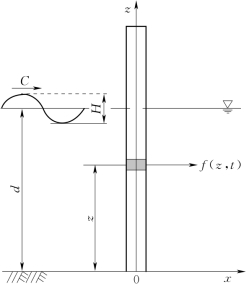
图5-2　小尺度直立柱体波浪力计算的坐标系统

作用在柱体任意高度z处的水平波浪力包括两部分：一部分为流体流过桩柱时由于黏性作用在柱壁产生的阻力和在柱后产生涡旋而引起的阻力，其与波浪水质点运动的水平速度ux密切相关，故称为水平拖拽力fD或速度力；另一部分为流经桩柱的流体由于物体的存在而引起流体运动的加速或减速所产生的力，即波浪水质点运动水平加速度d ux/d t引起的水平惯性力fI，或称为质量力[11]。

波浪作用在柱体上的拖拽力与波浪水质点的水平速度的平方和单位柱高垂直于波向的投影面积成正比。波浪作用在柱体上的质量力与等效柱体体积的水体质量和加速度成正比，还应考虑柱体附近附加水体的影响。

基于上述分析，作用于直立柱体任意高度z处单位柱高上的水平波浪力为[11]

对于圆柱体，式（5-38）可进一步转化为

式中 D——圆柱体直径。

由式（5-39），为了准确计算桩柱体的波浪力需要确定两大类变量，其一为根据所在位置的水深、波高和波浪周期选择合适的波浪理论来得到波浪质点的速度和加速度；其二为选取合理的拖拽力系数CD和惯性力系数CM。

拖拽力系数CD和惯性力系数CM应根据波浪和海流的参数以及杆件的形状、粗糙度（海生物）、尺寸和方向来确定。与结构物表面相对粗糙度ε=k/D、雷诺数Re、流—波速度比V1/Umo、杆件的方位有关。其中V1代表海流在波浪方向的分量，Umo是由二维波浪理论得出的在波峰处水质点的最大水平速度。

自莫里森公式提出以来，已有不少学者对CD和CM进行了大量的模型试验和现场观测工作，给出了系数的一些取值范围和确定方法。这些方法被一些行业标准引用并应用于实际工程中，下面介绍挪威船级社DNV规范中给出的系数确定方法。

拖拽力系数CD和质量力系数CM为雷诺数Re、KC常数和结构杆件相对粗糙度的函数。雷诺数Re、KC常数的定义分别为

式中 D——杆件直径；

Umax——静水位下水质点的最大速度；

v——运动黏滞系数；

Ti——波浪周期。

稳定流下，相对糙率k/D决定了系数CDS，其表达式为

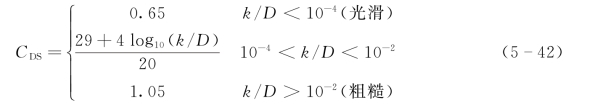
对于刚刚加工完毕未加涂层的钢材和涂刷油漆的钢材均可视为光滑。对于混凝土和高度锈蚀的钢材，可假定k=3mm。对于海生物生长状态下的杆件，可取值k=5～50mm。

CD可根据KC常数和系数CDS来计算，即

式中 ψ——尾流放大系数，可由图5-3查得。

图5-3中给出了光滑杆件（实线）和粗糙杆件（虚线）对应的曲线，中等糙率的杆件可根据两条曲线进行插值计算。

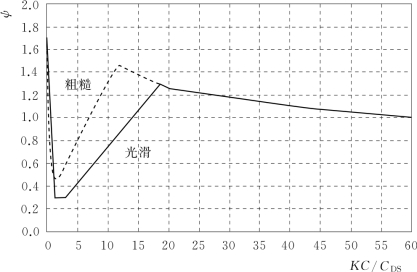
图5-3　ψ与KC的关系[12]

对于质量力系数CM，当KC＜3.0时CM=2.0；当KC＞3.0时计算为

当波浪可忽略不计稳定流的影响或KC＞30的大波浪情况下，根据上述方法可确定杆件表面光滑和粗糙两种极端情况下系数CD和CM的取值，结果如表5-18所示。

表5-18　CD和CM取值

2.桩柱波浪荷载

根据莫里森方程和波浪力计算系数的确定方法可以进行桩柱体波浪荷载的计算。下面首先介绍垂直杆件波浪荷载的计算，然后介绍任意倾斜杆件波浪荷载的计算方法。

取如图5-2所示的坐标系统，根据式（5-39）得到作用于单个圆柱体柱高d z上的水平波浪力为

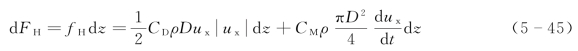
为了得到作用在某一段柱体（z2-z1）上的水平波浪力，可将上式从高度z1到z2积分，即(www.xing528.com)

当z1=0，z2=d+η时（η为波面高度），可得到整个柱体上的总水平波浪力为

根据式（5-47）可以得到整个柱体上的总水平力矩为

总水平波浪力作用点距海底的距离为

以上是直立柱体上的波浪力计算，海上测风塔基础结构通常还包含倾斜柱体构件。对于倾斜柱体上的波浪力计算，其方法在概念上与直立柱体的典型莫里森方程式是相同的，后者可视为前者的一种特殊情况。对于任意倾斜柱体，建立如图5-4所示的坐标体系。

就沿x方向传播的二维波浪的情况而论，在柱体上任一点处，与柱轴正交和相切的水质点的速度Un、Ut和加速度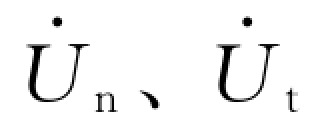是由波浪水质点的速度u和加速度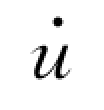组成的。由于波浪水质点的速度分量和加速度分量的大小是不同的，使得速度u和加速度u·虽同在zox平面内，但不在一条线上，因此由拖拽力和惯性力叠加的总力，就必须写成矢量形式，即

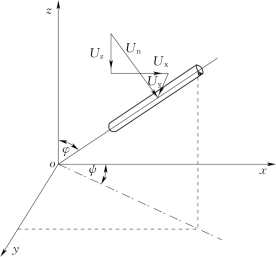
图5-4　倾斜柱体波浪力计算的坐标系统[11]

设e为沿柱轴线的单位矢量，对于直角坐标系，则有

速度矢量Un可由下面三重矢量积得到，即

式中 u——波浪水质点的速度矢量，其在3个坐标轴上的投影为{Ux，Uy，Uz}。

对于二维波浪Uy=0，有

结合莫里森方程，单位长度上桩柱体波浪力的一般形式可表示为[11]

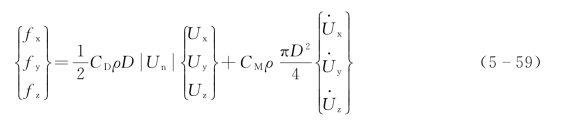
若计算整个倾斜柱体上的总波浪力，可由式（5-45）或式（5-59）沿整个柱长积分得到，但由于在某一时刻位于柱轴不同高度z处的水质点的速度和加速度不是处在同一相位，故沿柱长积分通常需采用数值积分的方法来实现。

3.破波力

当海上测风塔基础结构位于破波区时，破碎波，特别是卷破波将对基础结构物产生非常大的冲击作用，因此破碎波对桩柱结构的作用力是海洋工程和近岸工程中一个十分重要的问题。同行进波相比破碎波的作用力要显著地增大，问题的处理也复杂得多。由于破碎波产生的破波力为一历时很短的冲击力形式，这使得对破碎波进行详细研究变得非常困难。以下介绍JTS 145—2—2013给出的一种简化分析方法。

该方法是对5种底坡上的破波波浪力进行了试验进而得到的结果。它适用于浅水破波区中直立状态的小直径（D/L≤0.2）柱状结构物，当水底坡度i≤1/15时，作用在直立圆柱建筑物上的最大破波力F计算为

式中 H0——换算深水波高；

L0——深水波长；

D——杆件直径；

γ——海水重度；

A、B——系数。

式（5-60）中系数A、B值可查表5-19或查图5-5计算，其值可内插。

表5-19　系数A、B值与底坡i的关系取值[13]

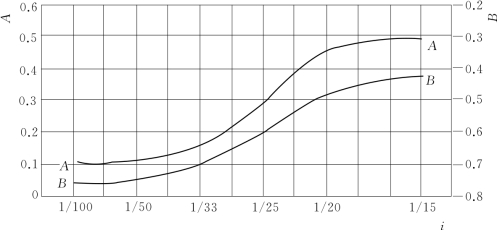
图5-5　系数A和B值与底坡i的关系[13]

计算水深为d，直立圆柱上最大破波力的作用点在水底面以上的高度l可计算为

式中 B3——与海底坡度有关的参数，当i≥1/20时，B3=1.4；当i≤1/33时，B3=1.2；当1/20＞i＞1/33时，可依据海底坡率进行线性内插。

实验表明，破波力随破碎点与桩柱相对位置的变化而变化。式（5-60）计算的破波力是最大破波力，出现于破碎点位于柱前深水一侧距离柱0.5～5倍破碎水深范围的某一位置，离开这一位置破波力迅速减小，出现最大破波力的位置随入射波波陡的增加而加大。