按照受风结构物的类别划分,测风塔风荷载由两部分组成,分别为测风塔塔架风荷载和测风塔基础位于海面以上部分所受风荷载。测风塔风荷载计算并不仅仅将上述两部分风荷载简单累加,相对单独的测风塔塔架,包含泥面以上测风塔基础结构后的整体塔架自振频率将产生显著变化,会使得测风塔风荷载增大。海洋环境中水位始终在变化,测风塔基础结构位于海面以上的高度也在不断变化,风荷载计算时应反映这一特性。
垂直于测风塔表面上的风荷载wk计算为
![]()
式中 βz——高度z处的风振系数;
μs——风荷载体型系数;
μz——风压高度变化系数;
w′0——经风压修正后的基本风压,k N/m2。
根据式(5-25)计算的风荷载按照测风塔迎风面积进行积分可求得风荷载合力,以下分别介绍该式中4个参量的计算方法。
1.基本风压
基本风压取决于风速和空气密度两个参量。风速可由临近气象站或海洋站的测风资料来推算,当无法取得风速资料时也可直接按照临近陆上基本风压来换算。空气密度可按式(1-17)或式(1-18)来计算,空气密度与海拔高度和温度相关,若进一步简化并忽略平均气温的影响,可近似计算空气密度为
![]()
式中 ρ——空气密度,t/m3;
z——所处的高度,m。
取得空气密度和风速后,基本风压w0计算为
![]()
式中 v0——离海平面10m高,50年一遇10min平均最大风速,m/s。
海上及海岛的基本风压,由于下垫面磨阻力的减小,使风压较陆上偏大。对沿海海面及海岛基本风压,应按邻近陆上基本风压乘以海上风压增大系数后采用。对于远离海岸的基本风压应乘以放大系数进行修正,修正后的基本风压w′0计算为
![]()
式中 η——修正系数,可按表5-13来取值。
表5-13 海上风压增大系数参照表[10]

2.风压高度变化系数
根据地面覆盖情况地面粗糙度可分为A、B、C、D等4类。对于远海海面和海岛的建筑物或构筑物,风压高度变化系数可按A类粗糙度类别确定。其风压高度变化系数μz可查表5-14或按照式(5-29)来计算。由于测风塔塔架底端至海面部分的基础高度通常在10~20m左右,故表中仅给出高度30m范围内的风压高度变化系数值。
表5-14 风压高度变化系数μz

续表

根据地面粗糙度指数和梯度风高度,除了查表计算外,A类粗糙度时风压高度变化系数计算为

式中 z——相对于海面的高度,m。
3.风荷载体型系数
海上测风塔塔架多由圆钢管或角钢构件焊接而成,在风荷载体形系数求解时,圆钢塔架的风荷载体型系数是在角钢塔架的风荷载体型系数基础上得到的。按照塔架体型和风荷载作用方向分为如图5-1所示的5类。

图5-1 塔架体型与风荷载作用方向
①~⑤—塔架体型与风向关系
对于角钢塔架的风荷载体型系数按表5-15取值。
表5-15 角钢塔架的风荷载体型系数[3]
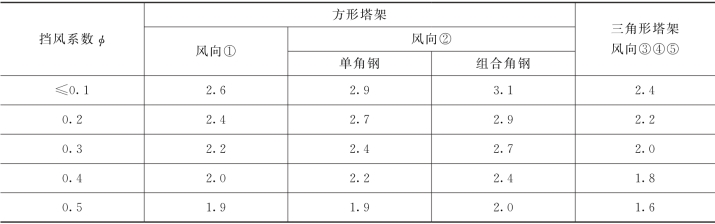
注:表中挡风系数φ=An/A,An为桁架杆件及节点挡风的净投影面积,A为桁架的轮廓面积。
对于圆钢塔架,直径d,修正后基本风压w′0,风压高度变化系数μz。若μzw′0d 2≤0.002,则圆钢塔架风荷载体型系数μs在角钢塔架对应的μs基础上乘以0.8采用;若μzw′0d 2≥0.0015,则圆钢塔架风荷载体型系数μs在角钢塔架对应的μs基础上乘以0.6采用;其余情况按插值法计算。(https://www.xing528.com)
上述为常用的桁架式塔架和基础结构的体形系数,由于圆筒形塔架应用较少,设计时可参照相关文献计算。
4.风振系数
对于结构物自振周期T1>0.25s的高耸结构,应考虑风压脉动对基础结构产生顺风向风振的影响。顺风向风振响应计算应按结构随机振动理论进行。风振系数计算为
![]()
式中 g——峰值因子,可取2.5;
I10——10m高度名义湍流强度,对应A类地面粗糙度,可取0.12;
R——脉动风荷载的共振分量因子;
Bz——脉动风荷载的背景分量因子。
脉动风荷载的共振分量因子R计算为

式中 kw——地面粗糙度修正系数,对A类地面粗糙度,可取1.28;
ξ1——结构阻尼比,对海上测风塔结构可取0.01,也可根据工程经验确定;
w0——考虑海面粗糙度后的基本风压;
f1——结构第1阶自振频率,Hz,为结构基本自振周期T1的倒数。
对于高耸结构,自振周期应通过模态分析来确定,简化情形下自振周期T1为
![]()
式中 T1——自振周期,s;
H——结构总高度,m。
对体型和质量沿高度均匀分布的高耸结构,脉动风荷载的背景分量因子Bz计算为
![]()
式中 φ1(z)——结构第1阶振型系数;
H——结构总高度,m,对A类地面粗糙度,H的取值不应大于300m;
k、a1——系数,对于高耸结构物k取1.276,a1取0.186;
ρx——脉动风荷载水平方向相关系数;
ρz——脉动风荷载竖直方向相关系数。
海上测风塔结构体型并不沿高度均匀分布,而是在迎风面和侧风面的宽度沿高度按直线或接近直线变化时,而质量沿高度按连续规律变化,因此应在式(5-34)计算的背景分量因子Bz基础上乘以修正系数θB和θV。系数θB为塔架在z高度处的迎风面宽度B(z)与底部宽度B(0)的比值,系数θV按表5-16确定。
表5-16 修正系数θV的取值[3]

脉动风荷载竖直方向的相关系数ρz计算为

式中 H——结构总高度,m,对A类地面粗糙度,H的取值不应大于300m。
脉动风荷载水平方向的相关系数ρx计算为
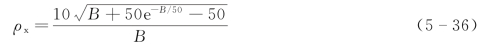
式中 B——结构迎风面宽度B≤2H,m。
对迎风面宽度较小的高耸结构,水平方向相关系数可取ρx=1。
式(5-34)中的振型系数φ1(z)应根据结构动力计算确定。对外形、质量、刚度沿高度按连续规律变化的竖向悬臂型高耸结构,振型系数φ1(z)也可根据相对高度z/H按表5-17确定,H为结构物总高度。
表5-17 振型系数φ1(z)[3]
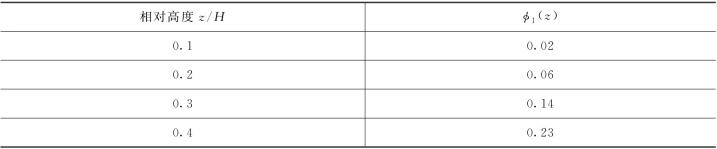
根据海上测风塔结构的动力分析结果,按照结构变形特点对高耸结构可按弯曲型考虑,除了查表外也可采用以下近似公式计算结构的振型系数φ1(z),即

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




