海上测风塔基础设计：简化流函数求解过程

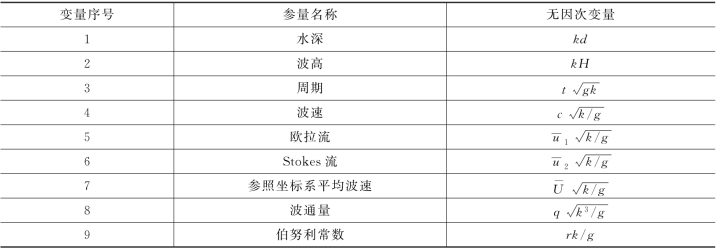
流函数的求解过程往往非常复杂，John.D.Fenton（1988）提出了一种无量纲化的流函数求解方法，从而极大地简化了流函数的求解过程[9]。首先将流函数求解中各几何变量和物理变量进行无量纲化转换，9个变量的名称和转化表达式如表4-4所示。

表4-4　变量的无量纲化表示

对于如图4-10所示的求解坐标系，波浪波动传播问题可视为一沿着海床水平的且不变形态的二维波浪波动，坐标系（x，y）的原点位于海底，波以速度c沿着x轴正向传播。设存在一移动速度为c的参照坐标系（X，Y），对于两个坐标系下的几何变量和速度变量存在关系式为

式中 t——时间；

u——静止坐标系下的水平速度；

v——静止坐标系下的竖向速度；

U——参照坐标系下的水平速度；

V——参照坐标系下的竖向速度。

为了完成问题的求解，所需要的方程数量和方程表达式如下：

（1）方程1。将无量纲的两个参数水深kd和波高（幅）k H通过波浪的波高与水深比值联系起来，建立的关系式是恒成立的，即

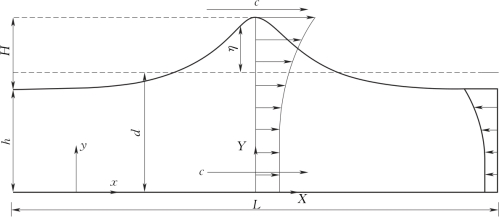
图4-10　流函数求解的坐标系

或者，当波长L已知时，将无量纲化的k H与H/L联系起来，可见

由于波速c事先未知，它取决于移动参照坐标系所依赖的速度，设参照坐标系下的平均水平流速为-U-，则在静止坐标系中时域平均速度可表达为

式（4-106）和式（4-107）是平行关系式，二者只选其一来计算。(www.xing528.com)

以上方程是所有质点均需要满足的条件，以下两个方程式（方程7和方程8）将波面离散化成N+1个节点所得到的结果，其中N为傅里叶求解的阶数，如图4-11所示。

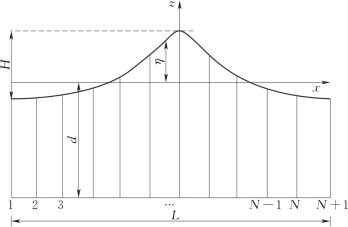
图4-11　离散化波面

非线性波面边界条件在波面每一个节点处都应该满足，一个周期内波面共存在N+1个节点，这些计算节点应在波峰与波谷间水平均匀分布。这些点相对于平均水面的距离由ηm=η（xm），m=0，1，2，…，N来表示，其中η0表示波峰的相对高度，ηN表示波谷的相对高度。根据平均水位的定义可知波面各点相对距离的总和为零。

（7）方程7。将波面各点上述特性进行归纳可表示为

（8）方程8。波高等于波面中波峰与波谷之间的高度差，即H=η0-ηN，从而存在恒成立的表达式为

（9）方程9及其他方程。根据流体运动学边界条件，采用流函数在海底处的表达式和在水面处[Y=d+η（X）]的表达式，即

根据流体动力边界条件，采用流函数表达时应满足波面处为零，此时在自由表面处伯努利方程可表示为

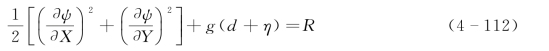
式中 R——常量。

符合式（4-110）～式（4-112）所有条件的流函数可设定为

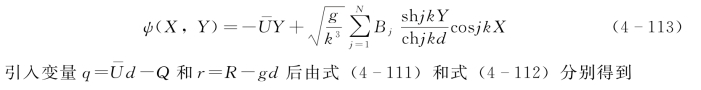
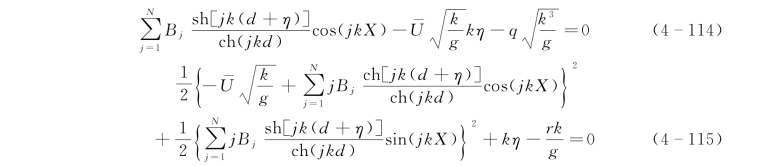
结合图4-11所示的波面分割点，运动学表面边界条件应该在N+1个节点上均适用。其中k Xm=mπ/N（m=0，1，2，…，N），由式（4-114）进一步可得到

类似的，结合图4-11所示的波面分割点，动力学表面边界条件应该在N+1个节点上均适用。其中k Xm=mπ/N（m=0，1，2，…，N），由式（4-115）进一步可得到方程式，即

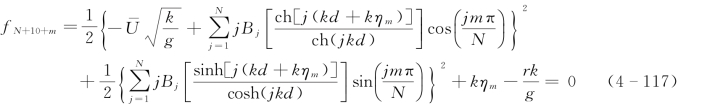
至此对于流函数的求解问题，上述方法共得到2N+10个方程，同时含有2N+10个未知量，故可以进行求解计算，最终得到表4-4中全部变量，同时可得到图4-11所示各点对应的kηj（j=0，1，2，…，N）值和系数Bj（j=0，1，2，…，N）。