海上测风塔基础设计：基本原理与方程

线性波是一种最简单的波浪求解理论，该理论基于众多假定条件而提出，这些假定条件包括[1]：

（1）流体是无黏性不可压缩的均匀流体。

（2）流体作有势的运动。

（3）重力是唯一的外力。

（4）流体表面上的压强等于大气压。

（5）海底为水平的固体边界。

（6）波幅或者波高相对于波长是无限小的，流体质点的运动速度是缓慢的。

按上述6条假定的最后一条，可以认为波动的自由表面所引起的非线性影响可以忽略，即非线性的自由表面运动边界条件和动力边界条件可以简化为线性的自由表面边界条件。

在重力场中处于平衡的液体的自由面为一平面。如果在某处外来干扰的作用下，液体自由表面的各个质点将离开其平衡位置，但失去平衡状态的各液体质点在重力和惯性力的作用下，有恢复初始平衡位置的趋势，于是形成了液体质点的振荡运动，并以波的形式沿整个表面传播。对于势波，只要得到波动海域的速度势φ便可求得各点的速度，因此研究势波的问题归结为寻求波动海域的速度势φ。

对于如图4-2所示的海域R，其速度势应满足拉普拉斯方程，即

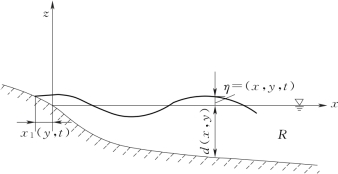
图4-2　波动海域R示意图[1]

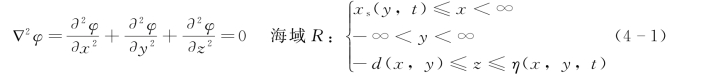
式中 x、y、z——笛卡尔坐标变量；

xs（y，t）——t时刻海域和陆域交线上的x坐标；(www.xing528.com)

η（x，y，t）——自由水面的铅直位移；

d（x，y）——水深变量函数。

由于式（4-1）边界约束条件中函数xs（y，t）和函数η（x，y，t）均为未知函数，因此拉普拉斯方程的求解域不仅随时间而变，而且本身也是要求解的一部分。对于线性波，为了能唯一确定速度势φ，所需要的边界条件包括海域底部运动边界条件、自由表面运动边界条件和自由表面动力边界条件。

采用势函数表示的海域底部运动边界条件为（变量d为水深）

采用势函数和波面函数表示的自由表面运动边界条件为

采用势函数和波面函数表示的自由表面动力边界条件为（g为重力加速度）

式（4-3）和式（4-4）所描述的边界条件可以合并为

综上可知，常深度下二维线性波的速度势φ（x，z，t）由以下基本方程和边界条件所确定，即

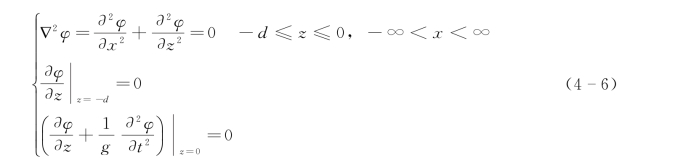
因为研究的是随时间作简谐振动的周期解答，显然可以不考虑初始条件，可以从设定一个反应时间周期性变化的速度势来进行分析。