特征波与分布在海上测风塔基础设计中的应用

鉴于波浪的随机特性，在进行波浪研究和分析时通常假定其为平稳随机过程和各态历经随机过程。平稳随机过程确保样本实测记录的时间起点不影响推求结果，各态历经随机过程保证了采用任意一个样本均可代表总体。关于特征波的一些统计分布特性均是基于这两个前提而得出的。

根据不同的统计分类标准，可以采用不同的特征波表示方法。对于特征波的定义，欧美国家多采用部分大波的平均值，苏联多采用超值累积概率法，我国港口与海港工程领域多采用超值累计概率法，我国海上石油工程领域多采用部分大波法。

当采用部分大波法时，平均波采用和表示，指波列中所有波浪的平均波高和平均周期。有效波采用H1/3和T1/3表示，分别指按照波高大小次序排列后，取前面1/3部分波的平均波高和平均周期。1/10大波采用H1/10和T1/10表示，分别指按照波高大小次序排列后，取前面1/10部分波的平均波高和平均周期。最大波采用Hmax和THmax表示，指波列中波高最大的波浪和其周期。

当采用超值累积概率法时，HF指在波列中超过此波高的累积概率为F对应的波高大小，常用的波高类型包括H1%、H4%、H5%和H13%等。

当波谱为窄带谱时，波面分布服从正态概率分布，波高分布服从瑞利分布，进而可以理论上分析得出不同波高分布与平均波高的关系。

对于深水波，累计概率特征波高HF与平均波高的关系为[16]

不同累计概率下特征波高HF与平均波高的具体比值如表3-7所示。

表3-7　累计概率波高与平均波高关系[2]

在浅水区域，考虑浅水效应后累计概率特征波高HF与平均波高H-的关系为[16]

其中

式中 erf——误差函数。

部分大波波高H1/p与平均波高的具体比值如表3-8所示。

表3-8　部分大波波高与平均波高关系[2]

在浅水区域，考虑浅水效应后部分大波波高H1/p与平均波高的关系为

无论是基于深水波波高的瑞利分布还是浅水下波高的格鲁霍夫斯基分布，波高值的上限都是无限的，而在工程实际中最大波高均为有限值。当最大波高作为一个随机变量，其与波高样本个数N0和波高分布形式有关。结合波高平均值与有效波波高的关系H1/3=1.598，最大波高的众值、均值和累积率μ%对应的最大波高与有效波高关系[17]如下：(www.xing528.com)

众值最大波高（Hmax）m为

均值最大波高为

式中 γ——欧拉常数，γ≈0.5772。

累积率为μ%的最大波高（Hmax）μ%为

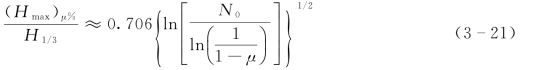
对于浅水条件下，最大波高与平均波高的关系更为复杂，可以参考相关文献。

波浪的波长服从瑞利分布，则根据线性波中波浪波长与周期的关系，可得到周期T的分布。其分布函数为[17]

统计数据表明，波浪周期的概率密度函数的离差系数CV≈0.283，偏态系数Cs≈0；而波高的离差系数CV≈0.552，偏态系数Cs≈0.635。可见周期的分布比波高的分布更集中（周期的离差系数CV更小），且几乎是对称的（周期的偏态系数接近0），因此波浪周期中出现机会最多的是平均周期。

海浪由深水进入浅水后，平均周期几乎不变。浅水周期的分布规律与水深无关，且变化很小。不同累积频率波高对应的周期是不同的，但它们只是统计出来的大致规律，理论关系还未完全确定。为简化起见，一般均将设计周期采用平均周期。对于大的波高，其波周期的分布比较集中于平均周期附近；对于较小的波高，其波周期的分布就比较分散。亦即，对于大的波高，一般不会遇到比平均周期大得很多的波周期；而对于小的波高，则有可能遇到比平均周期大得多的波周期[3]。

若当地大的波浪主要为风浪，可由当地风浪的波高与周期的相关关系外推与该设计波高相对应的周期，或按表3-9确定相应的周期。

表3-9　风浪的波高与周期的近似关系[18]

当地大的波浪主要为涌浪或者混合浪时，可采用与波浪年最大值相对应的周期系列进行频率分析，确定与设计波高为同一重现期的周期值。

日本的合田良实根据现场实测资料，统计得出波浪周期的相互关系为

在工程上，也可以近似按照如下关系式来确定波浪周期[16]，即

一般最大波高Hmax和最大波周期Tmax并不一定对应同一个波，其他特征值下的波高与周期也不一定对应同一个波，但在工程上二者往往配对使用。