汽车工程应用力学：掌握粘性流基础知识

1.两种流态——层流与湍流

雷诺实验

英国物理学家奥斯本·雷诺在做如图5-13所示的有关圆管中流体流动的实验时，发现有两种不同的流态：层流和湍流。实验做法如下：

水箱1装有普通水，杯4装有带颜色的水。先打开阀3，让普通水流出；后打开颜色水阀门，让颜色水一同流过玻璃管2。当阀门3开度小，保持水较低流速时，玻璃管2内的颜色水始终保持一条界限分明的纤流；若将颜色水细管移到另一位置时，仍然可以看到另一条同样的纤流，它与周围的普通水不相混合，如图5-13a所示。这表明玻璃管内的水只作一种层状流动，各层质点互不掺混，这种流动状态称为层流流动。

当逐步开大阀门3，流速增大到某一临界值时u_c′，管内颜色水纤流开始呈波纹状，如图5-13b所示；当继续开大阀门增大流速时，颜色水纤流破散并迅速与周围的清水掺混，使玻璃管的整个断面都带颜色，如图5-13c所示，表明此时水微团的运动轨迹极不规则，各层微团相互掺混，不仅沿流动方向的位移，而且还沿垂直于流动方向的位移，其流速的方向和大小随时间而变化，呈现一种杂乱无章的状态，这种流动状态称为湍流（亦称紊流）。

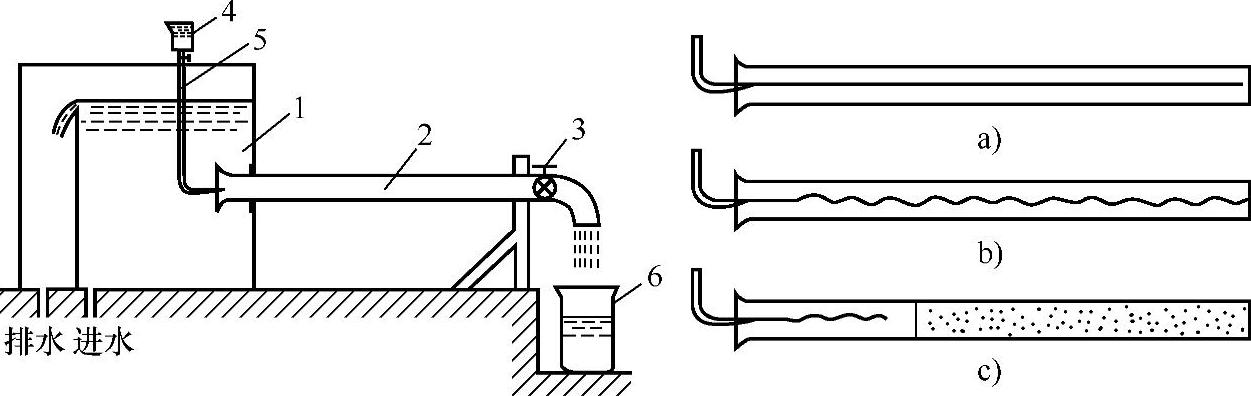
图5-13 雷诺试验

a）层流 b）层流向湍流的过渡状态c）湍流

1—水箱 2—玻璃管 3—阀门 4—颜色水瓶 5—细管 6—量筒

若按相反的顺序进行以上实验，即先开大阀门3，使玻璃管内为紊流，然后逐渐关小阀门3，则上述现象将以相反过程重演。所不同的是由紊流转变为层流的临界流速值u_c小于由层流转变为紊流的临界流速值u′_c，所以u_c称为下临界流速，而u′_c称为上临界流速。

雷诺及其以后的一些实验发现上临界界流速很不稳定。如果实验时存在某些起始扰动，则在较低流速下，层流就能变为紊流；反之，若流体在进入管道前具有相当平静的起始条件，即水箱水位恒定、管道入口平顺、管壁光滑、阀门开启轻缓的条件下，则层流可保持到很高的流速，此时u_c′比u_c大许多，这说明在一定条件下，层流向紊流过渡可存在一个较高的上临界流速u_c′，其数值大小随扰动的排除程度而提高。

但下临界流速u_c则是稳定的，它不受起始扰动的影响，对任何起始紊流，当流速u小于u_c值时，只要管道足够长，流动终将发展为层流。就实际工程来说，扰动是普遍存在的，所以上临界流速u_c′对工程实际没有意义，而下临界流速u_c却成为判断流态的界限，因此下临界流速u_c也就直接被称为临界流速。

2.流态的判别准则——临界雷诺数

从雷诺实验看，临界流速可以判别层流和紊流两种流态，但是直接用临界流速来判断流态并不方便，因为临界流速本身是随管道尺寸和流体种类、温度等条件而改变的。

雷诺等人曾对不同管径的圆管和多种液体进行实验，发现流动状态不仅与流速u有关，还与管径d、流体的动力粘度μ和密度ρ有关。若流动原来处于层流状态，其中的u、d、ρ越大，越容易成为紊流；而μ越大，越不易成为紊流。由这四个有量纲物理量进行乘除可组成一个无量纲数——雷诺数Re（关于量纲概念请看下一节），即

式中 u——圆管横截面上流体的平均速度（m/s）；

d——圆管直径，又称特征长度（m）；

ν——运动粘度（m²/s）。

据此，一定温度的流体在一定直径的圆管内以一定的速度流动，就可计算出相应的Re值。显然，Re越大，流动就越容易成为紊流；Re越小越容易成为层流。实验表明，尽管不同条件下的下临界流速u_c不同，但对于通常使用的管壁粗糙的平直圆管内的直匀流来讲，任何大小管径和任何牛顿流体（如水、汽油、所有气体），与它们的下临界流速u_c所对应的下临界雷诺数Re_c都是相同的，即

下临界雷诺数Re_c是不随管径和流体物理性质变化的无量纲数，实用上称为临界雷诺数。需说明的是：与上临界流速u_c′对应的上临界雷诺数Re_c′，由于其值不固定，在工程上缺乏实用意义，所以以后不再讨论。

雷诺及后来的实验都得出，临界雷诺数Re_c一般稳定在2000左右，其中以施勒（Schill-er）的实验值Re_c=2300得到公认。运用临界雷诺数Re_c作为流态判别标准，应用起来十分简便，只需计算出管流的雷诺数Re值，将其与临界雷诺数Re_c=2300对比，便可判别流动属于何种流态，如：

Re＜Re_c，流动是层流；

Re＞Re_c，流动是紊流（湍流）；

Re=Re_c，流动是临界流。

雷诺数Re无量纲，其物理意义是：流体运动时，作用在流体微团上的惯性力与其所受到的粘性力之比。即

当Re＜Re_c时，流动受粘性作用控制，使流体因受扰动所引起的紊动衰减，使流动保持为层流；随着Re的增大，粘性作用减弱，惯性对紊动的激励的作用增强，到Re＞Re_c时流动受惯性作用控制，流动转变为紊流。正因为雷诺数表征了流态决定性因素的对比，具普遍意义，因此所有牛顿流体（如水、汽油、所有的气体）圆管流的临界雷诺数Re_c=2300。

[例1]有一直径d=25mm的室内上水管，管内流速u=1.0m/s，水温t=10℃。

1）试判断管中水的流态；2）若使管内保持层流状态的最大流速是多少？

解：1）由表3-1查得10℃时水的运动粘度ν=1.31×10^-6m²/s，管中雷诺数为

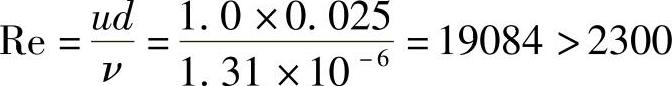
Re>Re_c，此管中的水流是紊流（湍流）。

2）保持层流的最大流速是临界流速u_c由式（5-21）得

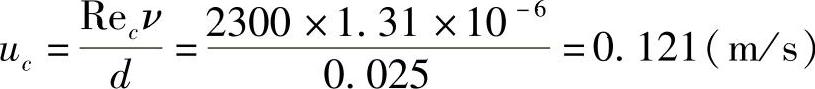
[例2]某低速送风管道，直径d=200mm，管内风速u=3.0m/s，空气温度t=30℃。1）试判断风道内气体的流态；2）该风道的临界流速u_c是多少？

解：1）由表3-2查得30℃时空气的运动粘度ν=16.6×10^-6m²/s，管中雷诺数为

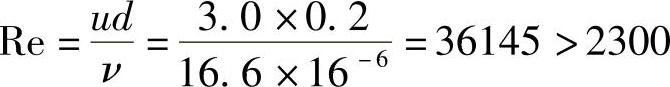
Re＞Re_c，此管中气体的流态是紊流。

2）保持层流的最大流速是临界流速

由以上两例可见，水和空气在管路内的流动一般为紊流。

3.层流向紊流的转变过程

自然界和工程中的绝大多数流体的流动都是紊流（也称为湍流）。

层流区别于紊流的根本在于层流各流层间互不掺混，质点（或微团）层次分明地向前运动，只存在粘性引起的各流层间的滑动摩擦力；而紊流则有大小不等的涡体动荡于各流层间，除了粘性阻力以外，还存在着由于质点掺混、互相碰撞所造成的惯性阻力。因此，紊流阻力比层流的要大得多。层流向紊流转变是与涡体的产生联系在一起的。图5-14绘出了涡体产生的过程。

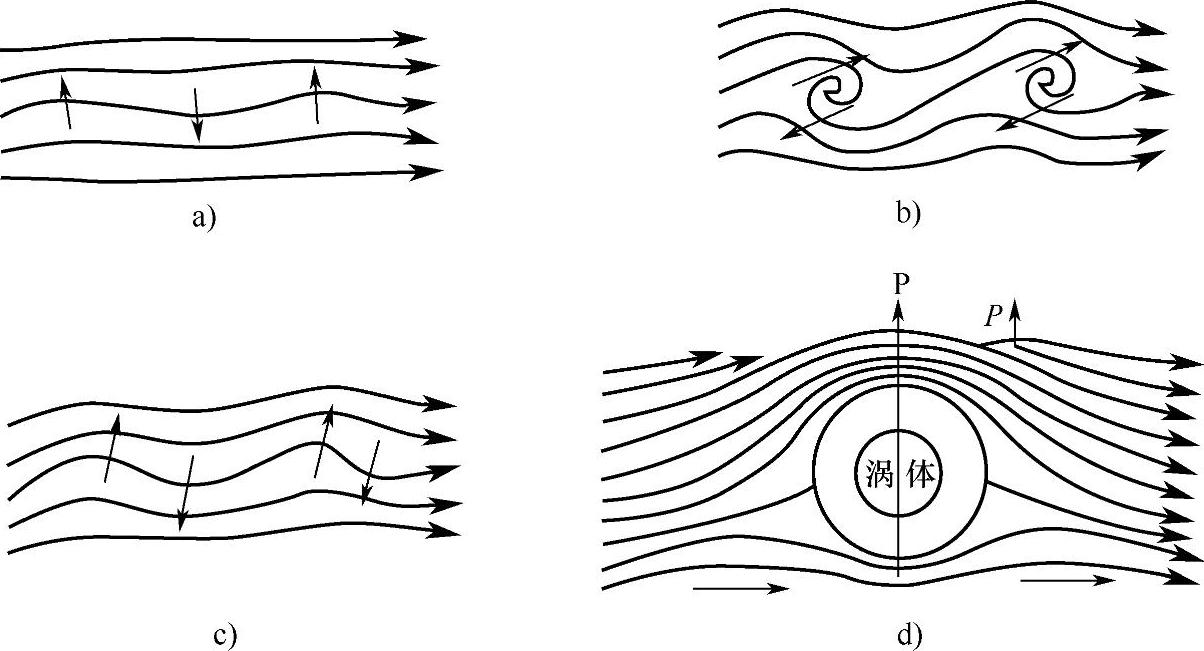
图5-14 层流向紊流的转变过程

a）～d）涡体产生顺序

流体流动从层流转变为紊流的过程，是一个复杂的过程。涡体的形成以及形成后的涡体脱离原来的流层掺入到邻近的流层，是层流转变成紊流不可缺少的两个条件。

涡体的形成有两个基本前提：一个是流体的物理性质，即流体具有粘性。实际流体过流断面上流速分布总是不均匀的，因此使各流层之间产生内摩擦切应力。对于某一选定的流层来讲，如图5-14中粗线所示，流速较快的流层对它的切应力是顺流向的，流速较慢的流层对它的切应力是逆流向的。因此该选定的流层所承受的切应力，有构成力矩促成涡体产生的倾向。另一个前提是流体的波动。设流体原来作直线运动。由于外界的微小干扰或来流中残存的扰动，流层将不可避免地发生局部性的波动，如图5-14a所示。在波峰一侧，由于流线间距的变化，使波峰凸面处的微小流束过流断面面积受到压缩而减小，流速增大，压强降低；在波谷凹面一侧的微小流束，过流断面面积增大，流速减小，压强增大。因此流层受到图5-14b中箭头所示的压差作用。当波幅增大到一定的程度后，由于横向压力和切应力的综合作用，使波谷与波峰重叠，终于发展成涡体，如图5-14c所示。(www.xing528.com)

涡体形成后，在涡体附近的流速分布将有所改变，如图5-14d所示。原来流速较大的流层，其流动方向与涡体旋转的方向一致，致使该流层的流速增大，压强减小；而原来流速较小流层，其流动方向与涡体的旋转方向相反，致使该流层的流速减小，压强增大。其结果导致涡体两侧有压差产生，形成横向升力（或下沉力），从而有可能推动涡体脱离原流层而掺入到流速较快的流层，这就是产生紊流掺混的原因。但是，此时还不一定就能产生掺混，进而发展为紊流。因为一方面涡体由于惯性作用，有保持其本身运动方向的倾向；另一方面流体有粘性，对于涡体运动产生阻力，因而约束涡体运动。所以，只有当促使涡体横向运动的惯性力超粘性力时，涡体才能够脱离原流层掺入新流层，从而发展为紊流。亦即，层流受扰动后，当粘性的稳定作用起主导作用时，扰动就受到粘性的阻滞而衰减下来，层流才会稳定；当扰动占风时，粘性的稳定作用无法使扰动衰减下来，层流就变为紊流。由此可见，流动呈现什么流态，取决于扰动的惯性作用和粘性的稳定作用相互效量的结果，因此表征运动流体的惯性力与粘性力的比值——“雷诺数Re”是可以用来判别流态的。

4.附面层

流体绕物体运动，简称绕流。绕流有多种形式：或者是流体绕静止物体运动，例如风绕建筑物流动；或者是物体在静止的流体中运动，例如船艇在湖泊中航行；或者是物体与流体出现相对运动，例如汽车在有风的情况下行驶等。所有这些绕流可以看成同一类型绕流问题。

流体在绕过物体运动时，其摩擦阻力主要发生在紧靠物体表面的一个速度梯度很大的流体薄层内，这个薄层即为附面层（或称边界层）。附面层有内边界和外边界，内边界（固体边界）即为物体的表面，外边界即为附面层与主流接壤处。在实际流体流过物体时，不管流动的雷诺数有多大，固体边界上的流速必为零，沿内边界的外法线上的速度从零迅速增大，直至外边界，流速才与未扰动的主流速度u₀相接近。一般规定在速度到达99%主流速度u₀处为附面层的外边界。附面层内的流体由于存在着一个很大的速度梯度，因此流体的粘性作用是不可忽略的；附面层以外的流动区域，粘性作用可以忽略，可按理想流体来处理。

为了说明附面层内的流动特征，图5-15给出了一个最典型的例子，即在二维恒定匀速流场中放置一块与流动平行且静止的水平锋锐平板。由于平板是不动的，根据无滑移条件和流体的粘性作用，与平板接触的流体质点的流速都要降为零。在平板附近的流体质点由于受到平板的阻滞作用，流速都有不同程度的降低。离平板越远，阻滞作用越小。当流动的雷诺数很大时，这种阻滞作用只反映在平板两侧的一个较薄的流层内，这个流层就是附面层（边界层）。

图5-15 平板表面的附面层

a）在雷诺数较小的流体中 b）在雷诺数较大的流体中

关于附面层的厚度，严格地讲，附面层的外边界应在法线方向的无穷远处，因为物面对流体的影响是逐渐消失而不是突然终止，流速也应在无穷远处才能真正达到主流速度u₀。但根据实验观察，在离平板表面一定距离后，流速就非常接近来流的速度u₀。因此一般规定u_x=0.99u₀的地方作为附面层的界限，附面层的厚度就是根据这个界限来定义的，用δ表示。附面层的厚度与雷诺数成反比。在雷诺数较小时，附面层较厚，且向前延伸；雷诺数较大时，附面层较薄。在汽车空气动力学有关分析研究中，大多数是在雷诺数很大的情况下进行，这时附面层的厚度与物面长度相比是个小量，对于汽车而言，附面层厚度只不过是几毫米到几十毫米而已。

实际上附面层内、外区域并没有明显的分界，规定速度达主流速度的99%处为附面层的外边界是为了方便研究问题；这个边界线不是流线，流体可以出入边界层。

附面层的存在是容易通过实验得到证实，有时甚至用肉眼就可以观察到。例如，船只在静水中航行时，可以观察到在贴近船侧表面有一条狭窄的水带跟着船一起运动，越往外水的速度越小，在远离船的水域里，水是不动的。

5.附面层内的流态

附面层内的流动也存在两种流态——层流和湍流。附面层分为层流附面层和湍流附面层两部分，这两者之间为一小段的过渡附面层，如图5-16所示。在附面层的前部，由于厚度δ较小，流速梯度很大，但粘滞切应力也很大，这时附面层内的流动属层流，称为层流附面层。附面层内沿平板x方向某一位置流动的雷诺数Re_x（当地雷诺数）可表示为

式中 x——从该位置到平板前缘的距离。

图5-16 平板附面层内的不同流态

当雷诺数达到一定数值时，附面层内的流动经过一段过渡流后转变为湍流，成为湍流附面层。由层流附面层转变为紊流附面层的位置x_c点称为转折点，亦称转捩点，该点的雷诺数为临界雷诺数Re_xc。

在湍流附面层区域内，可能还会产生气流分离现象，气流离开分离点后不再贴附物面流动而成为涡流。因此，从物面分离后的气流不再适用附面层理论。值得提示的是，压强p在附面层内沿y方向几乎不变，即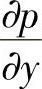=0。

在附面层内，在同一法线上，物面上的压强与附面层外边界上的压强相等。这就是所谓的“压力穿过附面层不变”的附面层特性。

6.量纲与无量纲量概念

（1）量纲的概念 在空气动力学中涉及各种不同的物理量，如长度、质量、力、速度、粘性系数……等，所有这些物理量都是由自身的物理属性（或类别）和相关的规定量度单位两个因素构成的。例如长度，它的物理属性是线性几何量，度量单位规定有米、厘米、英尺……等。

物理量的属性（类别）称为量纲或因次。显然，量纲是物理量的实质，不含有人为的影响。通常以L代表长度量纲、M代表质量量纲、T代表时间量纲等，采用[q]代表某物理量q的量纲，则有。

面积A的量纲

[A]=L²

密度ρ的量纲

[ρ]=M/L³

单位是人为的度量标准，例如现行的长度单位米。因为有量纲量是量纲和单位两个因素决定的，因此含有人为的意志影响。

量纲分为基本量纲和导出量纲。例如长度量纲L、时间量纲T均为基本量纲，而速度的量纲是导出量纲，即[u]=L/T。为了应用方便，并同国际单位制相一致，普遍采用基本量纲系，即选取质量M、长度L、时间T、温度θ为基本量纲；对于不可压缩流体运动，则选取M、L、T作为三个基本量纲，其他物理量的量纲均为导出量纲。例如：

速度[u]=LT^-1

加速度[a]=LT^-2

力[F]=MLT^-2

动力粘度[μ]=ML^-1T^-1

综合以上各量纲公式可得出，某一物理量q的量纲[q]都可用三个基本量纲的指数乘积形式表示，即

式（5-23）称为量纲公式，物理量q的性质（属性）由量纲指数α、β、γ决定：

当（α=0，β≠0，γ=0）——q为几何量

（α=0，β≠0，γ≠0）——q为运动学量

（α≠0，β≠0，γ≠0）——q为动力学量

（2）无量纲量 当量纲公式（5-23）中各量纲指数均为零时（即α=β=γ），则[q]=1，物理量q是无量纲量，也就是纯数，如圆周率、角度等。无量纲量可由两个具有相同量纲的物理量之比得到，也可由几个有量纲物理量进行乘除组合，使组合物理量的量纲指数为零而得到，例如对有压管流，由断面平均速度u、管道直径d、流体的运动粘度ν组合为

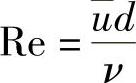
其量纲

所以Re是无量纲量，它由3个有量纲量进行算术的乘除组合而得到的，称为雷诺数（Reyn-olds number）。

根据无量纲数的定义和构成，可归纳出无量纲量具有以下特点：

1）具有客观性。正如前面指出，凡有量纲的物理量都有度量单位。同一个物理量，因选取的度量单位不同，数值也不同。如果用有量纲量作过程的自变量，计算出的因变量数值将随自变量选取单位的不同而不同。因此，要使运动方程式的计算结果不受人主观选取单位的影响，就需要把方程中各项物理量组合成无量纲项。从这个意义上说，真正客观的方程式应是由无量纲项组成的方程式。

2）不受运动规模影响。既然无量纲量是纯数，所以数值大小与度量单位无关，也不受运动规模的影响。规模大小不同的流动，如果两者是相似的流动，则相应的无量纲数相同。在模型试验中，常用同一个无量纲数（如雷诺数Re）作为模型和原型流动相似的判据。

3）可进行超越函数运算。由于有量纲量只能作简单的代数运算，进行对数、指数、三角函数等运算是没有意义的。只有无量纲化才能进行超越函数运算，如气体等温压缩功计算式

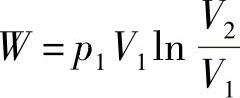
其中压缩后与压缩前的体积比V₂/V₁要组成无量纲项后，才能进行对数运算。