伯努利方程与流体动压变化关系

在定常流动、不可压缩的理想气流中，同一流线上每一点处的大气压力（静压力）p和动压力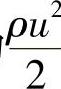之和总是等于一个常数C。即

式中 ρ——气体密度；

u——气体流速；

C——总压力或伯努利常数。如果汽车置于流场中，C值可由汽车远前方处的气流状态求得。

式（3-19）称为伯努利方程（亦称伯努利定律）。伯努利定律表明，当流线上各处的流速发生改变时，该处的大气压强也必须改变，但大气压强和动压强的总和保持一个常数。静压强与动压强是此消彼长的关系。伯努利定律是建立在理想流体和流体能量守恒的基础上，用来描述流体压强与速度之间的变化关系的。

伯努利定律的实用表明，汽车周围的流谱在汽车表面上因流速的不同而产生一个独特的压力分布。(www.xing528.com)

但必须指出，式（5-19）的常数C对无旋流与有旋流的用法有所区别：即如果在无旋流中，则全流场只有一个C值；如果在有旋流中，则每一条流线都有一个C值，流线改变了，C值也就跟着改变。

[例]在海拔为零的海边上，有直匀流流过一流线形很好的汽车。远前方直匀流的静压强p∞=101200N/m²，流速为100m/s。已知汽车外形前部上A、B两点的速度u_A=0，u_B=150m/s，求A、B两点的静压强。空气密度ρ=1.225kg/m³。

解：汽车前部的气流是无旋流，因此伯努利常数只有一个。根据远前方处的条件，其总压力值p₀为

于是有