前轮角阶跃输入下的瞬态响应探究

汽车的操纵稳定性同汽车行驶时的瞬态响应密切相关。

给汽车转向盘一个转角，使汽车由等速直线行驶转换为等速圆周行驶，这一转换的过渡过程便是一种瞬态，其相应的瞬态运动响应则称为转向盘角阶跃输入下的瞬态响应。在上述的稳态响应中，汽车的横摆角速度等运动参数是不随时间发生变化的；但瞬态响应却相反，汽车的运动参数将随时间发生变化，而且变化更为复杂，因此瞬态响应的优劣更能表征汽车的操纵稳定性。例如汽车的侧滑与侧翻，多发生在瞬态而非稳态。

图4-14为某一汽车等速行驶在t=0时，驾驶人急速转动转向盘至角度δ_swo，并维持此转角不变（即转向盘角阶跃输入）时的汽车的瞬态响应曲线。

图中的瞬态响应是以汽车横摆角速度ω_r的变化状况来描述的。从图4-14中可见，当给汽车以转向盘角阶跃输入后，汽车横摆角速度ω_r经过一过渡过程便达到了稳态横摆角速度ω_r0（即曲线由开始的明显起伏逐渐过渡到趋于平直），此段过渡过程横摆角速度的变化状况就是汽车的瞬态响应。瞬态响应的品质（亦即横摆角速度变化的优劣）将直接影响到汽车的操纵稳定性。

1.横摆角速度瞬态响应的特点

根据图4-14的横摆角速度的瞬态响应表现，可以看出它具有以下特点。

（1）反应时间滞后 汽车横摆角速度不能立即达到稳态横摆角速度ω_r0，而需要经过一段时间后才能第一次达到ω_r0。这一段滞后时间τ称为反应时间。反应时间短，则驾驶人感到转向反应迅速、及时，否则就会觉得反应迟钝。也有用到达第一峰值的时间ε来表示滞后时间。

（2）执行上有误差 最大横摆角速度ω_r1常常大于稳态横摆角速度ω_r0，表示执行指令有误差。我们把ω_r1/ω_r0×100%称为超调量，它表示执行指令误差的大小。

（3）横摆角速度波动 在瞬态响应中，横摆角速度ω_r以频率ω在稳定值ω_r0的上下波动。波动频率ω取决于汽车动力学系统的结构参数，它也是表征汽车操纵稳定性的一个重要参数。

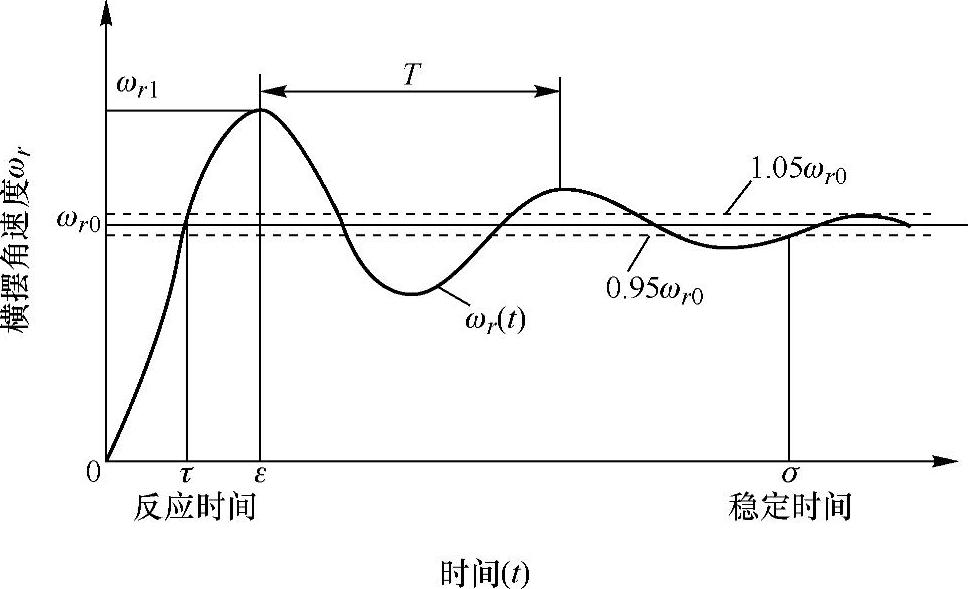
图4-14 转向盘输入—固定转角时横摆角速度的瞬态响应曲线

（ω_r（t）为瞬态时的横摆角速度随时间变化的曲线，ω_r0为达到稳态时的横摆角速度）

（4）进入稳态所经历的时间 上面所说的时间τ只是第一次达到稳态横摆角速度ω_r0的时间，但由于横摆角速度出现波动，待其处于稳态需要一段时间。我们把横摆角速度达到并稳定在稳态值ω_r0的95%～105%之间所需要的时间σ称为稳定时间。

个别汽车也可能出现汽车横摆角速度ω_r不能收敛的情况，即ω_r值越来越大，转向半径越来越小，而导致汽车产生“车头卷入”、后轴侧滑或翻车的危险。由此可知，瞬态响应的优劣应包括两方面内容：一是行驶的方向稳定性，即给汽车以转向盘角阶跃输入以后，汽车能否达到新的稳定状况；二是响应品质，即在达到新的稳定之前，其瞬态响应的特性是否好。

2.横摆角速度的瞬态响应

前轮角阶跃输入下的瞬态响应包括许多内容，但此分析只以横摆角速度为对象，因为它的响应特性具有特征性。当给前轮以角阶跃输入后，在过渡过程中汽车的横摆角速度ω_r随时间发生变化的状况——ω_r（t）曲线是如何呢？

二自由度汽车运动微分方程（4-1）包含了最重要的汽车质量与轮胎侧偏刚度等两方面的参数，所以最能反映汽车曲线运动的最基本特征。因此，我们在讨论横摆角速度瞬态响应时也离不开二自由度汽车运动微分方程，根据它来推导得出ω_r（t）的变化规律。现将二自由度汽车运动微分方程重写如下

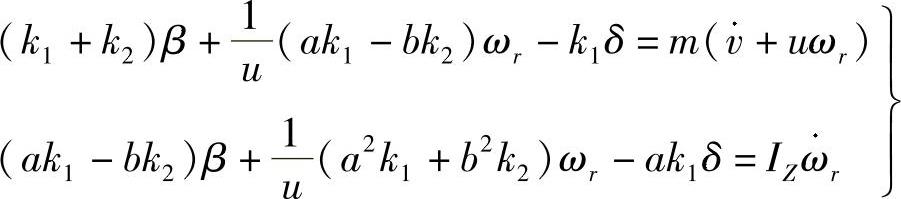
对二自由度汽车运动微分方程的第二式求出β值，并对β求导数，将导数值代入第一式；将代入第一式的结果，写成以ω_r为变量的形式，结果如下

上式是单自由度一般强迫振动微分方程式，通常写为

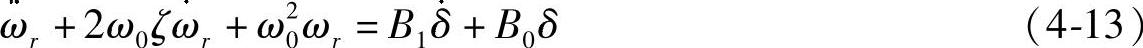
式中 ω₀——固有圆频率，；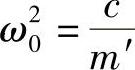

ζ——阻尼比，；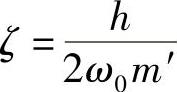

；

。

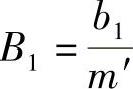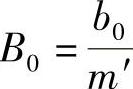当t＞0后，上式进一步简化为

式（4-14）是二阶常系数齐次微分方程，其通解等于一个特解与对应的齐次微分方程的通解之和。其特解为

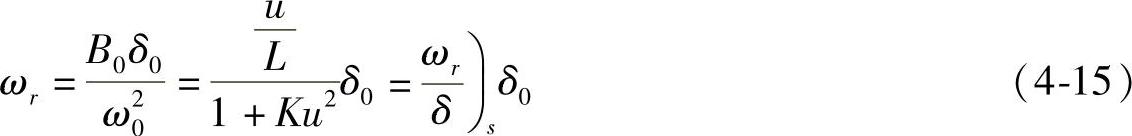
其对应的齐次微分方程为

齐次微分方程的通解为

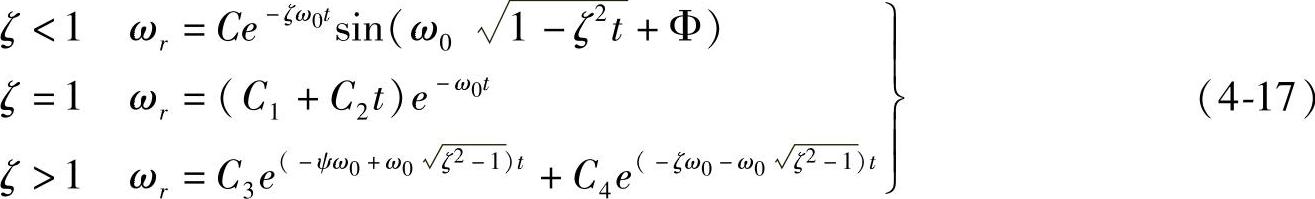
式中 C、Φ、C₁、C₂、C₃、C₄——均为积分常数，可根据运动初始的条件来决定。

ζ>1称为大阻尼，横摆角速度响应ω_r（t）是单边上升的。随着时间的增长，在开始，ω_r趋于稳态ω_r0；但当车速超过临界速度u_cr后，ω_r是发散的，趋于无穷大，此时汽车失去了稳定性。

ζ=1，称为临界阻尼，横摆角速度响应ω_r（t）也是单边上升，且趋近于稳态ω_r0。

ζ＜1，称为小阻尼，横摆角速度随时间t变化的函数ω_r（t）是一条向稳态ω_r0收敛的减幅正弦曲线（如图4-14所示）。

由于正常的汽车都具有小阻尼的横摆角速度瞬态响应，所以下面只讨论在角阶跃输入后，ζ＜1时的横摆角速度响应ω_r（t）的变化规律。

显然，在ζ＜1时，横摆角速度ω_r（t）等于方程（4-14）的特解与通解之和，即

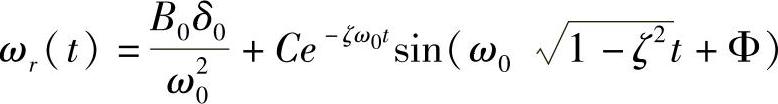
省略过程计算，得

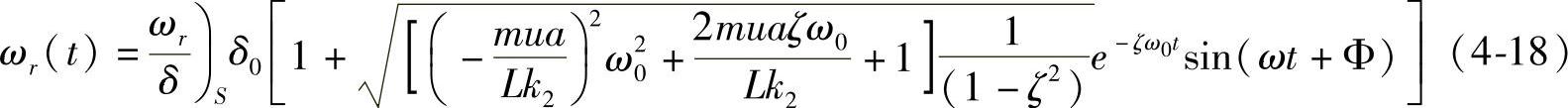
式（4-18）就是给汽车前轮一个角阶跃输入时，汽车的横摆角速度瞬态响应。由起始条件可知，在t=0时，ω_r=0。由式（4-18）可知，当t=∞时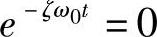，，ω_r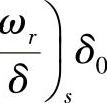（∞）==ω_r0，即横摆角速度最后趋于稳态横摆角速度ω_r0。当时间在零与无穷大之间时，ω_r（t）是衰减的正弦函数（参看图4-14）。显然，阻尼比越大，衰减越快。

[实例]图4-15为美国安全试验车（ESV）的横摆角速度瞬态响应在不同车速下的满意区域。试验时汽车以40km/h和110km/h的车速直线行驶，以不小于500°/s的角速度转动转向盘，转向盘转角预先估计好，要求汽车进入稳态时的侧向加速为0.4g。图4-15中，还给出了丰田安全试验车（ESV）的横摆角速度瞬态响应曲线。试验车的前轮转向角采用了两种计算方法：一种是直接采用前轮绕主销的转角，另一种是采用转向盘转角与转向传动比来近似换算。(www.xing528.com)

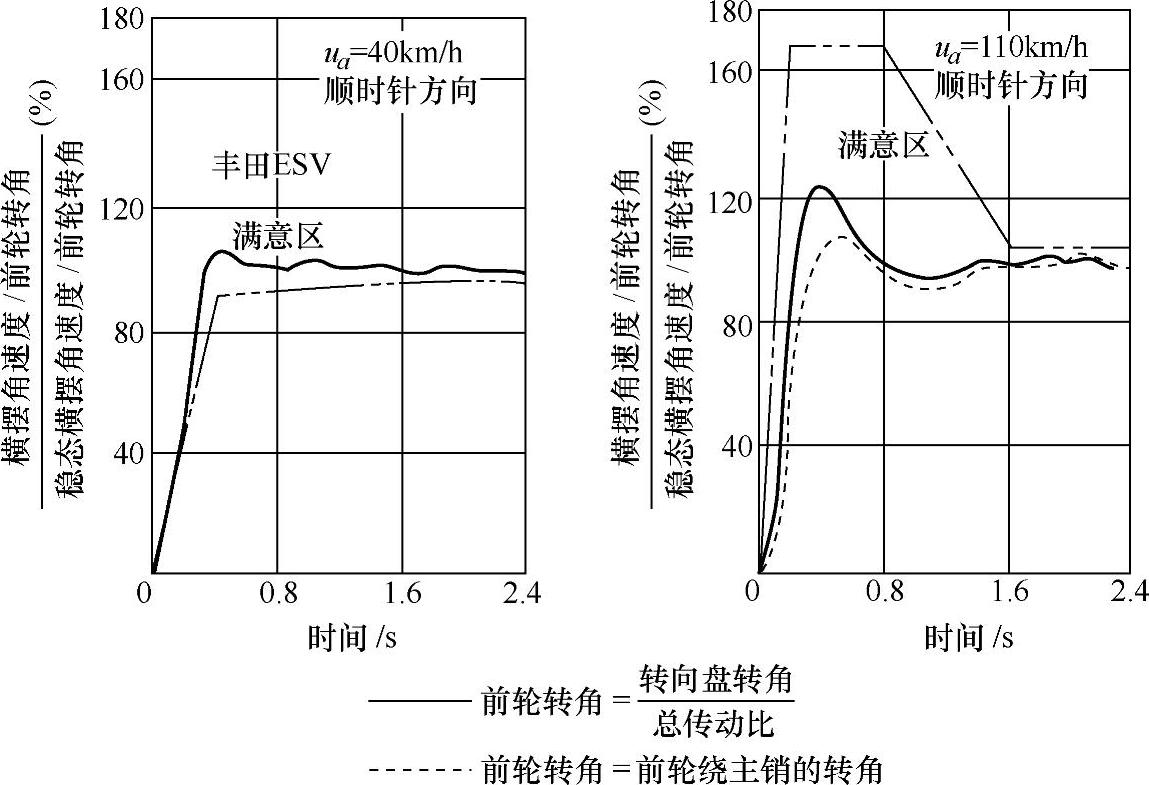
图4-15 美国安全试验车的横摆角速度瞬态响应满意区域和丰田ESV的横摆角速度瞬态响应曲线

3.表征瞬态响应品质的参数

瞬态响应品质的优劣可通过以下参数来表征。

（1）横摆角速度ω_r波动时的固有（圆）频率ω₀由二自由度汽车运动微分方程式（4-1）和式（4-13）可解得

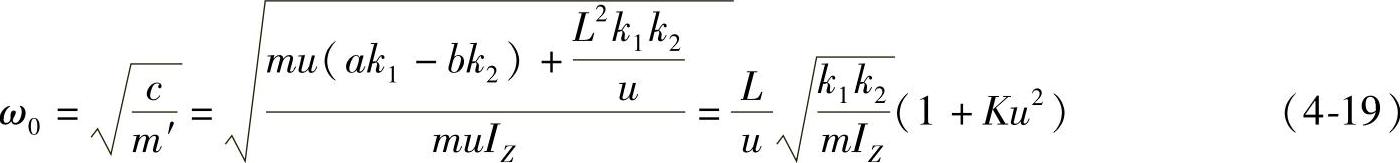
ω₀值是评价汽车瞬态响应的一个重要参数。ω₀值应高一些为好，这样可以减少谐振的倾向。固有频率f₀与固有圆频率ω₀的关系为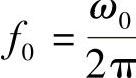。固有频率f₀的单位为赫兹（Hz）。图4-16为一些欧洲及日本轿车的固有频率f₀与稳定性因数K值，f₀值在1Hz左右。欧洲的高速公路最高限速较高，所以轿车车速较高，其固有频率f₀也较高，可在0.9Hz以上。

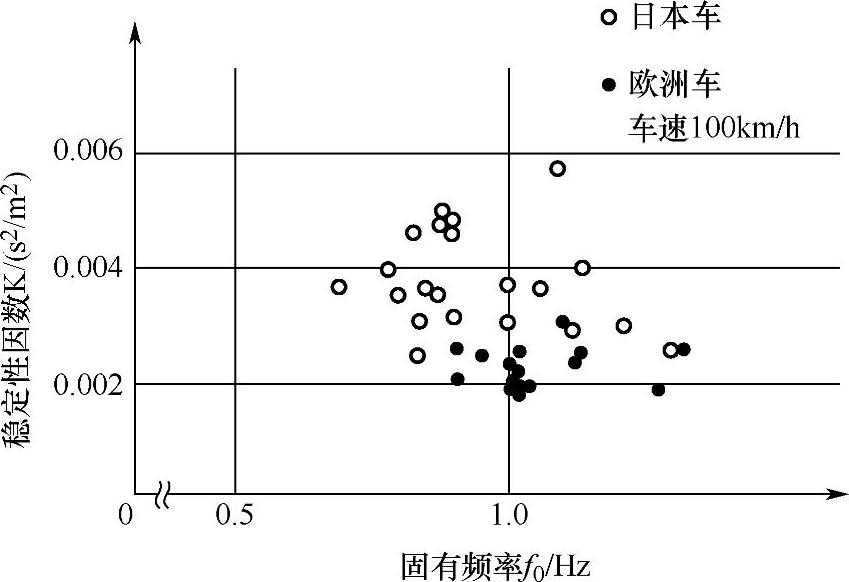
图4-16 一些欧洲及日本轿车f₀值与K值

图4-17给出了某型汽车的横摆角速度波动时的固有圆频率ω₀与汽车质m、轴距L、绕z轴的转动惯量I_z、车速u等参数的关系。其中车速u对横摆角速度波动时的固有频率ω₀影响较明显。

（2）阻尼比ζ由式（4-13）可知，阻尼比的表达式为

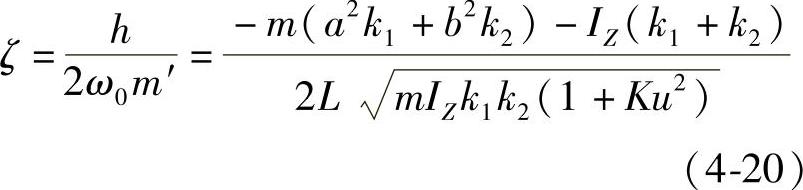
由式（4-20）可知，汽车的横摆角速度瞬态响应的阻尼比与许多参数有关。图4-18为汽车的一些参数对阻尼比的影响。

图4-19为不同阻尼比的横摆角速度瞬态响应曲线。从图中可见，阻尼比ζ=0.1时，横摆角速度ω_r值起伏大，稳定时间σ长；随着阻尼比逐渐增大，横摆角速度起伏逐渐趋缓，稳定时间逐渐缩短。随着时间的增长，曲线ω_r（t）是衰减的正弦函数（参看图4-14）。显然，阻尼比越大，横摆角速度的衰减越快，汽车的操纵稳定性就越好。

（3）反应时间τ反应时间是指给前轮角阶跃输入后，汽车的横摆角速度第一次到达稳定值ω_r0所需要的时间。τ是评价汽车瞬态响应的另一个重要参数。τ值应小些为好，其值小说明转向反应迅速、及时。

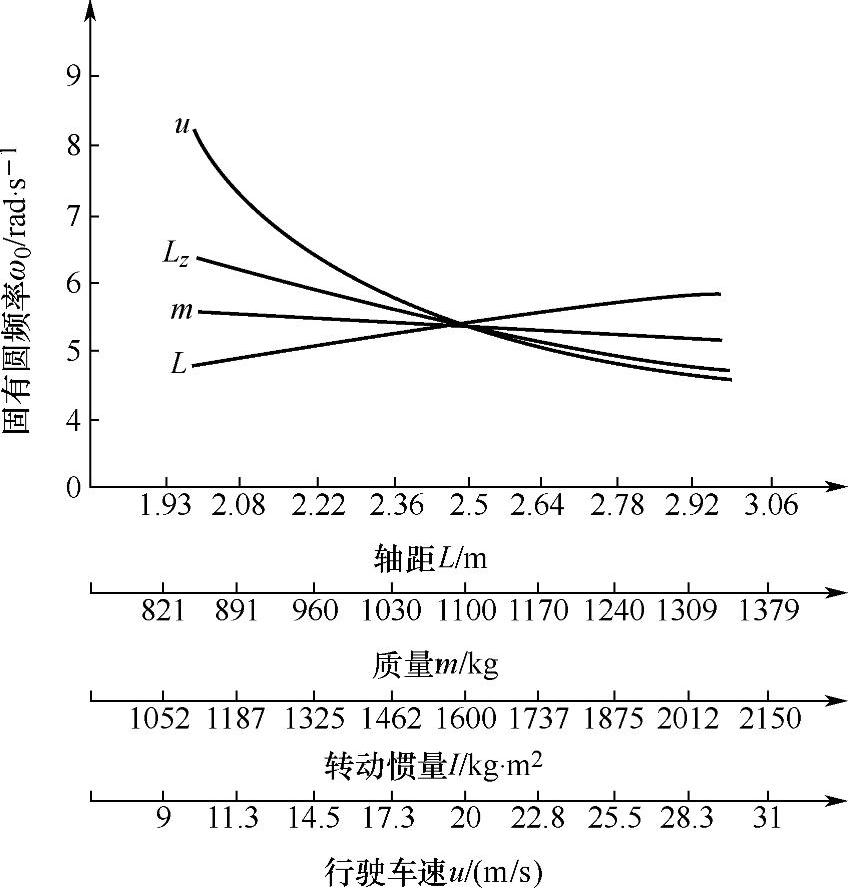
图4-17 汽车横摆角速度响应波动时的固有圆频率与汽车有关参数的关系

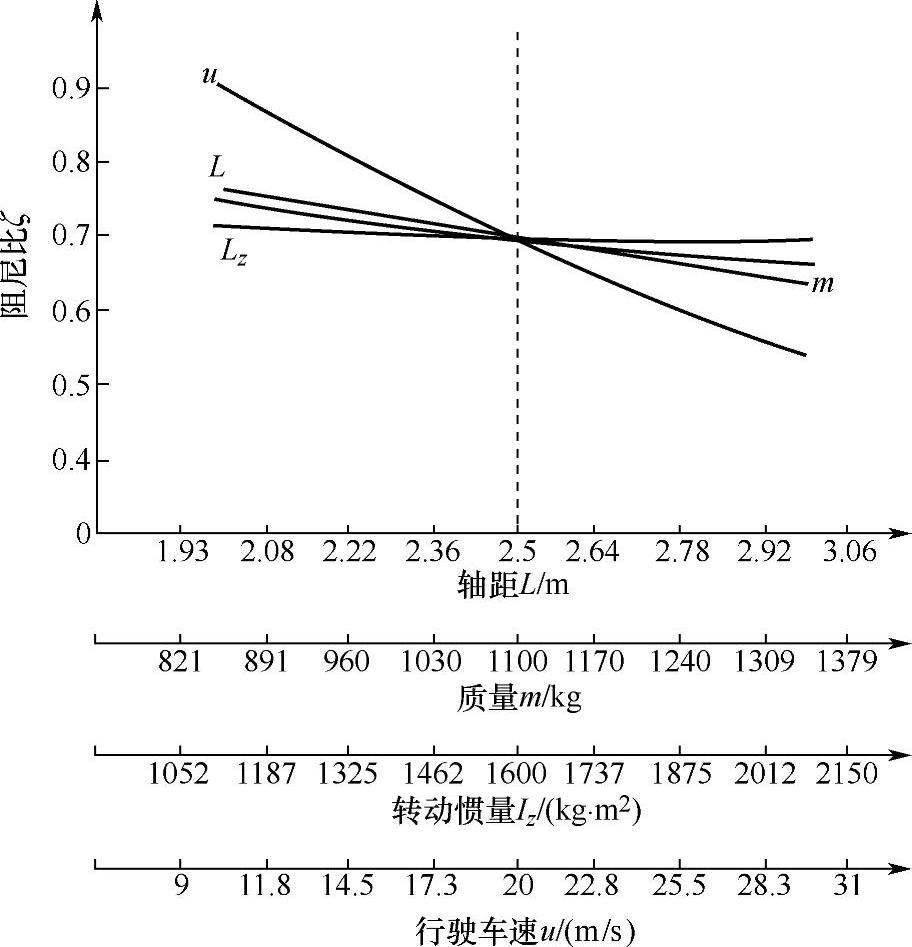
图4-18 汽车的一些参数与横摆角速度瞬态响应阻尼比的关系

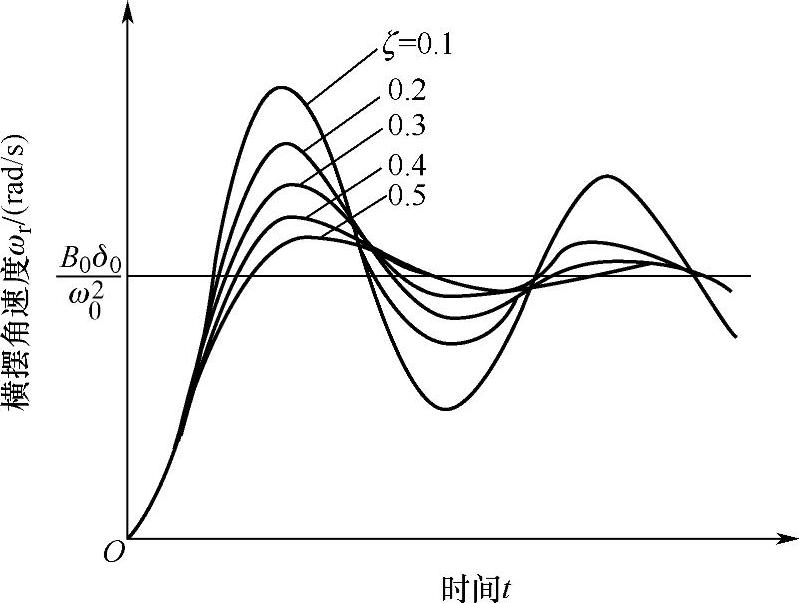
图4-19 不同阻尼比的横摆角速度瞬态响应曲线

图4-20给出了汽车几种有关参数的变化与横摆角速度瞬态反应时间τ的关系。

（4）稳定时间σ横摆角速度达到并稳定在稳态值的95%～105%之间所需要的时间称为稳定时间σ。

稳定时间表明瞬态响应到达稳态响应所经历的时间。因此，一般希望稳定时间应尽可能短。

以上推导出的ω₀、ζ参数表达式，是根据二自由度汽车模型的运动微分方程求得的，有很大的局限性，在数值上与实际有相当大的出入，仅供宏观分析作参考。

4.瞬态响应的稳定条件

上面讨论瞬态响应是以横摆角速度为对象，所以这里所讲的瞬态响应的稳定条件也就是指横摆角速度瞬态时的稳定条件。以上讨论的瞬态响应，其横摆角速度ω_r（t）为减幅的正弦函数，最后趋于一稳定值ω_r0，因此是稳定的。但有的汽车也可能出现不稳定，即横摆角速度ω_r（t）趋于无穷的情况。

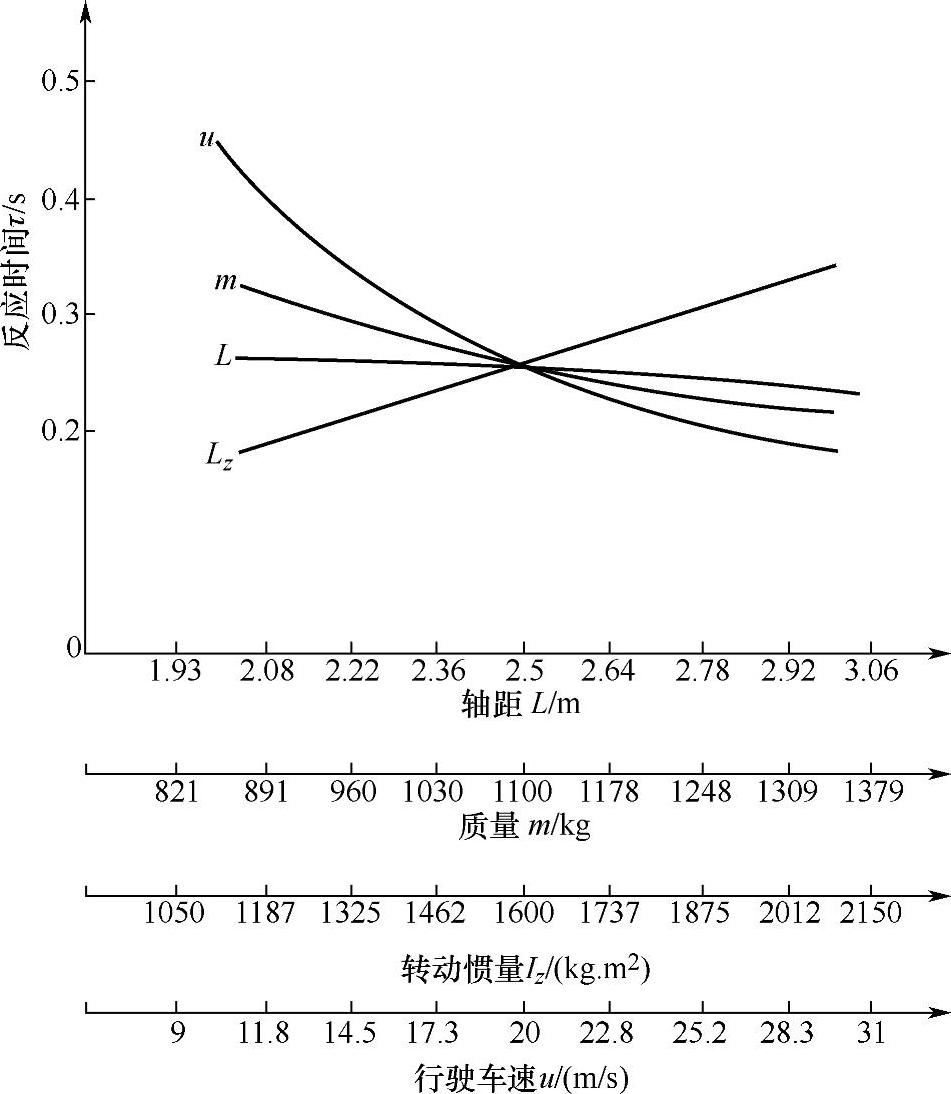
图4-20 汽车一些参数的变化对瞬态ω_r反应时间τ的影响

是否稳定，则取决于在前轮角阶跃输入下二自由度汽车的运动微分方程（4-13）所对应的齐次微分方程（4-16）的通解，亦即取决于汽车本身固有的特性。

根据齐次微分方程的通解（式4-17），横摆角速度瞬态响应是否稳定可从以下两方面来分析。

1）当ζ≤1时，只要ζω₀为正值，横摆角速度的瞬态响应就是一条收敛于稳态值的减幅正弦曲线，汽车是稳定的。ζω₀是否为正值呢？这可由下式来判断。即

根据式（4-12）、式（4-13）可知

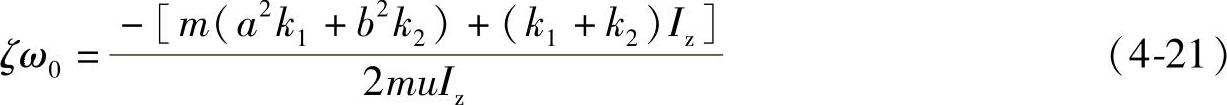
因为轮胎侧偏刚度k₁、k₂为负值，故ζω₀恒为正值。因此可以判定，当ζ≤1时，汽车在瞬态响应是稳定的。

2）当ζ＞1时，特征根必须为负值，齐次微分方程的解才收敛趋于零。换言之，ω²₀应为正值，汽车的横摆角速度才减幅收敛。但ω²₀是否为正值呢？这可由下式来判断。即

根据式（4-12）、式（4-13）可知

上式的右边第一项可能是正值、也可能是负值，是正值还是负值则由汽车稳态转向特性——是不足转向还是过度转向来决定。即

若汽车具有不足转向特性，则（ak₁-bk₂）＞0，式（4-22）中的右边第一项为正值，ω²₀为正值，可以判定汽车的横摆角速度能减幅收敛，汽车是稳定的。

若汽车具有过度转向特性，则（ak₁-bk₂）＜0，第一项为负值。但是，即使第一项是负值还不能决定ω²₀等于负值，还要看车速的快慢。当车速很慢时，即使第一项是负值，汽车横摆角速度ω_r（t）还是减幅收敛的，因为式中的第二项不仅恒为正值，而且在车速u很低时，分母值很小，此项的正值很大，式右边两项之和还是正值，使得ω²₀为正值。这就是我们在“汽车稳态转向特性”所说的，虽然汽车已潜在了过度转向特性，但车速在其临界速度以下或更偏于低速行驶时，也还是表现为不足转向，汽车还是稳定的。但是，当随着车速u的增加，第二项的正值则越来越小，ω²₀就可能为负值，ω_r（t）曲线将发散，汽车处于不稳定状态。

具有过度转向特性的汽车使ω²₀=0的车速称为临界车速u_cr。将ω²₀=0代入式（4-22），可求得过度转向的临界车速为

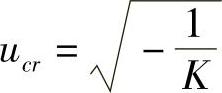
这和讨论稳态响应时所推导得出的临界车速是一样的。