汽车制动过程分析：值路面影响分析

利用β线与I曲线的配合，就可以分析前、后制动器制动力具有固定比值的汽车在不同φ值路面上的制动情况。分析的目的在于了解不同φ值路面对制动过程所产生的影响。

为了便于分析，首先介绍两组线组——f线组与r线组。f线组是后轮没有抱死，在不同φ值路面上前轮抱死时的前、后轮地面制动力关系曲线；r线组是前轮没有抱死，而后轮抱死时的前、后轮地面制动力关系曲线。汽车制动时，其中一车轴先抱死是常见现象，随后才是两车轴都抱死。例如普通轿车，随着制动踏板力的逐渐加大，常有后轮没有抱死而前轮先抱死这样的过程；又如有的空载货车，随着制动踏板力的逐渐加大，常有前轮没有抱死而后轮先抱死这样的过程。为什么会出现这种状况呢？主要原因在于“分配比例”是固定的，但路面的附着条件却千变万化，各车轴的制动效果也随之发生变化。

1.求f线组与r线组

（1）求f线组f线是描述只有前轮抱死时的前、后轮地面制动力的关系曲线。每一种φ值路面都有一根f线，几种不同φ值路面的f线便组成了f线组。f线组是根据下面的关系式绘制的。

前轮抱死的条件是：前轮地面制动力F_Xb1等于前轮附着力φF_Z1，即

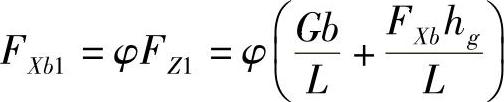
因为F_Xb=F_Xb1+F_Xb2，将此式代入上式，经整理得出：汽车在不同φ值路面上只有前轮抱死时的前、后轮地面制动力的关系式为

显然，当前、后轮都抱死时，式（3-14）亦成立，只是此时的后轮地面制动力亦已达到后轮附着力的数值。

以不同φ值代入式（3-14）作图，便得到f线组，如图3-39a所示。

下面来解读f线组：

1）f线组与纵坐标的交点为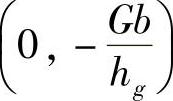，表明无论φ取任何值，f线组永远经过该点，即此交点与φ值无关。F_Xb2为负值时已是地面驱动力。

2）f线组与横坐标的交点依次为a、b、c、…，这些交点表明在后轮地面制动力F_Xb2=0的情况下，不同φ值路面所对应的前轮地面制动力F_Xb1的大小，即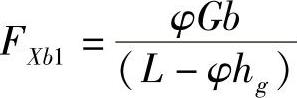。在这些点的情况下，总地面制动力只等于前轮地面动力，即

F_Xb=F_Xb1⁺⁰=F_Xb1＜φG

3）当f线越过交点a、b、c…以后，后轮地面制动力F_Xb2比前轮的F_Xb1增加得快。随着地面总制动力F_Xb的增加，最后f线与I曲线相交，在交点处后轮才达到抱死。交点处的F_Xb1+F_Xb2=F_φ1+F_φ2=φG（这也就是前、后车轮同时抱死的条件）。

4）f线与I曲线相交已表明前、后轮在此处己达到了都抱死的最佳制动效果，I曲线以上的f线段已无意义，不再去探讨。

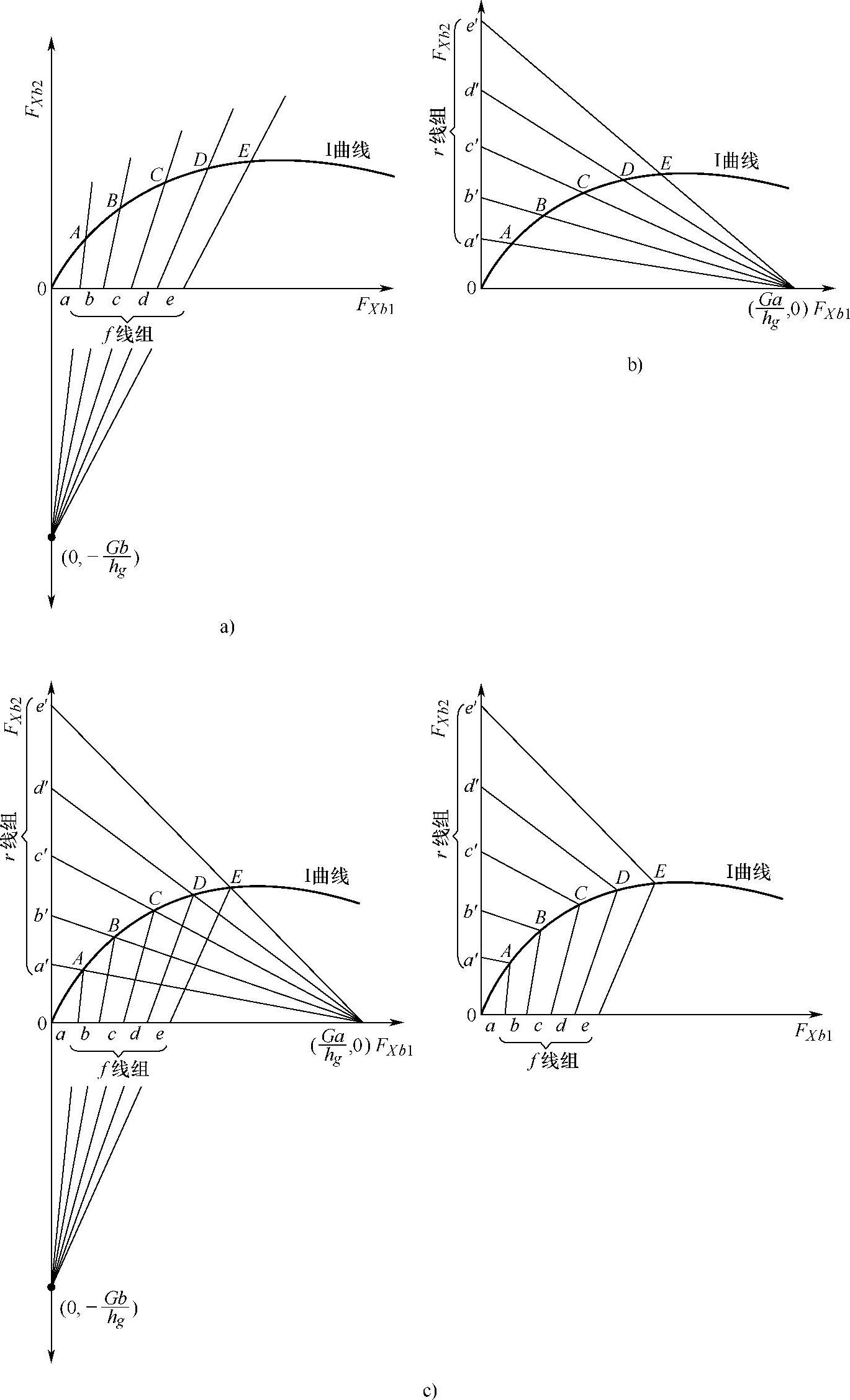
图3-39 f线组与r线组的绘制

a）f线组 b）r线组 c）f线组与r线组组合

（2）求r线组r线是描述只有后轮抱死时的前、后轮地面制动力的关系曲线。r线组是根据下面的关系式绘制的。

前轮抱死的条件是：后轮地面制动力F_Xb2等于后轮附着力φF_Z2，即

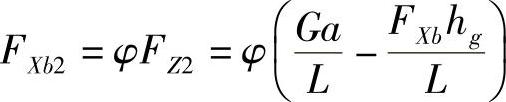
将F_Xb=F_Xb1+F_Xb2代入，经整理得出：汽车在不同φ值路面上只有后轮抱死时的前、后轮地面制动力的关系式为

(www.xing528.com)

显然，当前、后轮都抱死时，式（3-15）亦成立，只是此时的前轮地面制动力亦已达到前轮附着力的数值。

以不同φ值代入式（3-15）作图，即得到r线组，如图3-39b所示。

下面来解读r线组：

1）r线组与纵坐标的交点为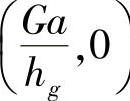，表明无论φ取任何值，r线组永远经过该点，即此交点与φ值无关。

2）r线组与纵坐标的交点依次为a′、b′、c′…，表明在前轮地面制动力F_Xb1=0的情况下，不同φ值路面所对应的后轮地面制动力F_Xb2的大小。在这些点的情况下，总地面制动力只等于后轮地面制动力，即F_Xb=0+F_Xb2＜φG。

3）在r线的交点a′、b′、c′…以下，随着F_Xb2的稍稍减小与相应的F_Xb1的增大，F_Xb也增大，最后r线与I曲线相交，在交点处前轮才达到抱死。交点处的F_Xb1+F_Xb2=F_φ1+F_φ2=φG

4）r线与I曲线相交已表明前、后轮在此处己达到了都抱死的最佳制动效果，所以I曲线以上的r线段已无意义，不再去探讨。

把f线组和r线组绘制在一起便得到如图3-39所示式样。

从图3-39可见，对于同一φ值的f线与r线的交点A、B、C、…既符合F_Xb1=φF_Z1，又符合F_Xb2=φF_Z2，所以这些交点便是前、后车轮都抱死（也包含同时抱死）的点。因此，连结A、B、C、…各点的曲线也就是前面所述的I曲线。

2.利用“四线”来分析不同φ值路面上的制动过程

下面，利用β线、I曲线、f和r线组来分析汽车在不同φ值路面的制动过程。参看图3-40，为了便于说明问题，以早期生产的ГAЗ-51货车为例，其同步附着系数为φ_O=0.39。图中还画上了F_Xb1与F_Xb2之和为0.1g或0.2g或0.3g…的45°斜直线组。同一根斜直线上的点均有同样大小的总地面制动力F_Xb，相应的制动减速度也是常数，即为0.1g或0.2g或0.3g…。故此45°斜直线组称为“等地面制动力线组”或“等制动减速度线组”。分析制动过程时，常利用此线组来确定制动过程中的总地面制动力与制动减速度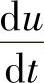的数值。

（1）φ＜φ_O时，总是前轮先抱死 假设φ=0.3，则制动开始时，前、后制动器制动力F_μ1、F_μ2按β线上升；因前、后车轮均未抱死，故地面地面制动力F_Xb1、F_Xb2也按β线上升。到了A点时，β线与φ=0.3的f线相交，前轮开始抱死，制动减速度为0.27g，此时的地面制动力F_Xb1、F_Xb2已符合后轮没有抱死而前轮先抱死的条件。若驾驶人继续增加踏板力，F_Xb1、FXb2将沿这条f线上方变化，前轮的地面制动力F_Xb1不再等于前制动器制动力F_μ1反而略大于F_μ1，略大的原因是由于继续制动引起汽车质心位置前移量增加、前轮地面法向反力增加所致。但因后轮尚未抱死，所以随着踏板力的增加，F_μ1、F_μ2沿β线上升，F_Xb2仍然等于F_μ2而继续上升。当F_Xb1、F_Xb2升至A′时，这条f线与I曲线相交，此时后轮才达到抱死所需要的地面制动力（亦即后轮的附着力），于是前、后车均抱死，汽车获得的减速度为0.3g。

由上述可见，β线位于I曲线下方（φ<φ_O），制动时总是前轮先抱死。

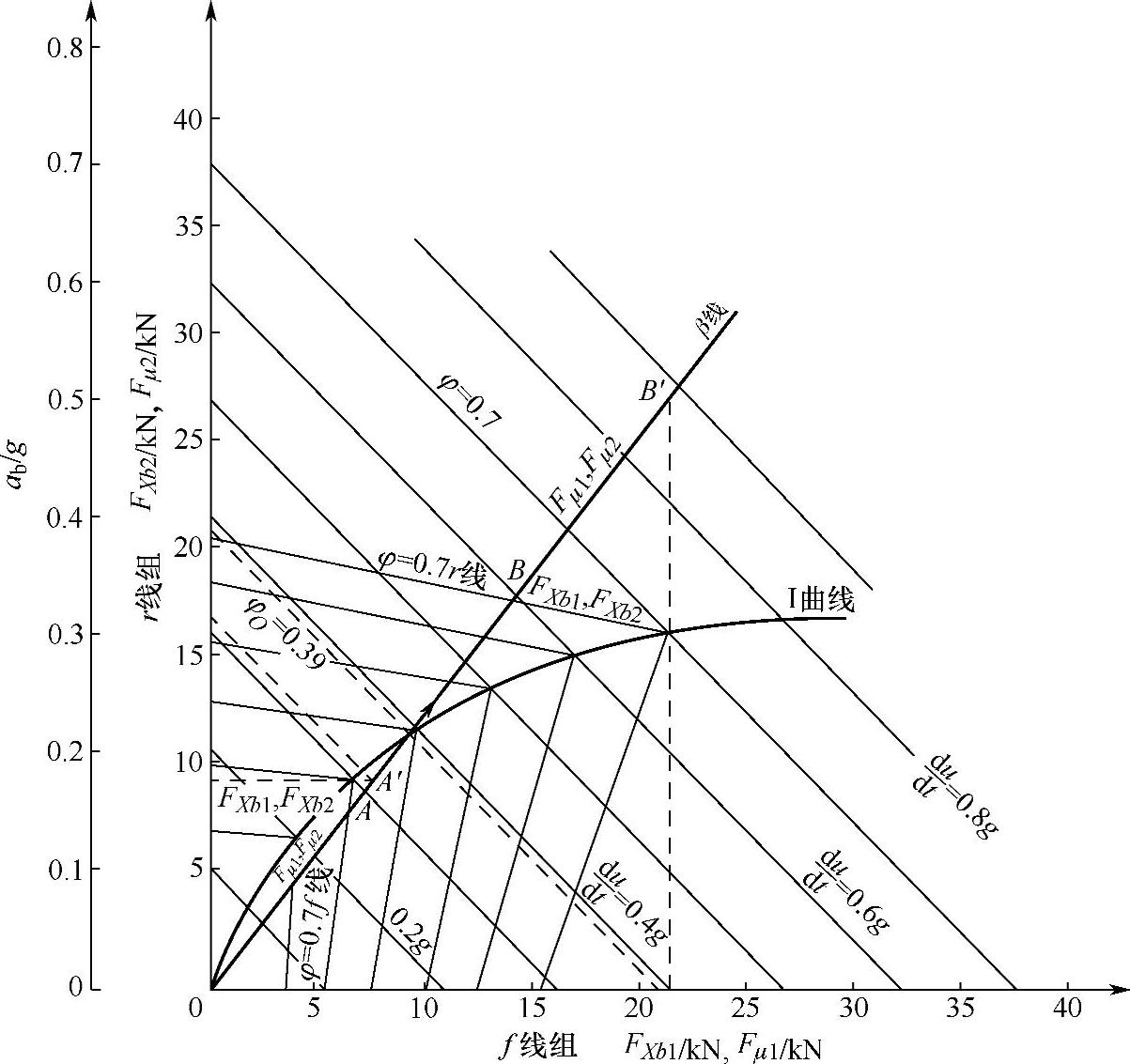
图3-40 在不同φ值路面上汽车制动过程的分析

（2）φ＞φ₀时，总是后轮先抱死 假设φ=0.7，则制动开始时，前、后车轮均未抱死，故前、后车轮地面制动力和制动器制动力均按β线增长。到达B点时，β线与φ=0.7的r线相交，地面制动力F_Xb1、F_Xb2符合后轮先抱死的条件，后轮开始抱死，此时的制动减速度为0.6g。从B点以后，再增加踏板力，F_Xb1、F_Xb2沿这r条线下方变化。但再继续增加踏板力，后轮的法向反力因质心位置前移量增加而有所减少，使后轮地面制动力沿r线略有下降。因前轮尚未抱死，当F_μ1、F_μ2沿β线继续增长时，始终存在F_Xb1=F_μ1。当F_μ1、F_μ2增长到B′点时，这条r线与I曲线相交，F_Xb1达到了前轮抱死所需求的地面制动力，于是前、后车轮均抱死，汽车获得0.7g的减速度。

由上述可见，β线位于I曲线上方（φ＞φ_O），制动时总是后轮先抱死。

（3）φ=φ_O时，前、后轮同时抱死 若φ=φ_O，制动开始后，F_μ1、F_μ2始终沿β线增长，并保持F_Xb1=F_μ1和F_Xb2=F_μ2；继续增加踏板力，直至β线与φ_O=0.39的f线和r线相交，此时汽车前、后轮同时抱死，汽车获得的减速度为φ_Og，即0.39g。

我们把以上汽车在三种不同φ值路面的制动过程总结为：

1）当φ＜φ_O时，β线位于I曲线下方，前轮先抱死。

2）当φ＞φ_O时，β线位于I曲线上方，后轮先抱死。

3）当φ=φ_O时，β线与I曲线相交，前、后轮同时抱死。

只要φ≠φ_O，要使两轮都不抱死所得到的制动强度总是小于附着系数，即Z<φ。