汽车工程应用力学：前后制动器力分配优化

1.理想制动力分配的工况选择

选择什么制动工况来作为理想制动力分配的研究对象？从以上分析可知，如果只有单根轴（前轴或后轴）抱死拖滑，作用于该轴的地面制动力已经达到了极限值；而尚未抱死拖滑的另一轴，只有通过驾驶人继续加大制动踏板力以增大此轴的制动器制动力才能相应获得较大的地面制动力，直至使该轴也抱死。然而，对于已经抱死拖滑的那根轴而言，此时驾驶人将制动踏板踩得再死也不可能继续增大此轴的地面制动力。根据这个原理可以判定：前、后车轮同时抱死拖滑时所产生的最大地面制动力所需要的整个制动系制动器制动力最小，亦即前、后车轮同时抱死拖滑所需的最大踏板力最小，制动系的效率最高。加上，前、后车轮同时抱死对汽车的方向稳定性比较有利，所以选择前、后车轮同时抱死工况来作为理想的前、后制动器制动力分配的研究对象。

2.理想的制动力分配I曲线的表达式

前面已指出，制动时前、后车轮同时抱死，对于附着条件的利用、制动时汽车的方向稳定性均较为有利。此时的前、后制动器制动力F_μ1和F_μ2的关系曲线，称为理想的前、后制动器制动力分配曲线（I曲线）。

在任何附着系数φ的路面上制动，前、后车轮同时抱死的条件是：前、后车轮制动器制动力之和等于附着力，并且前、后车轮制动器制动力分别等于各自的附着力。即

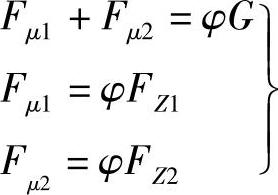
或

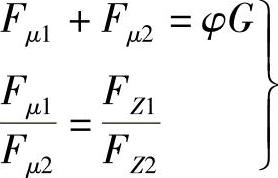
将式（3-9）代入上式，得

消去变量φ，将方程表达为F_μ2=f（F_μ1）的函数形式，即可得到理想的前、后制动器制动力分配关系表达式为

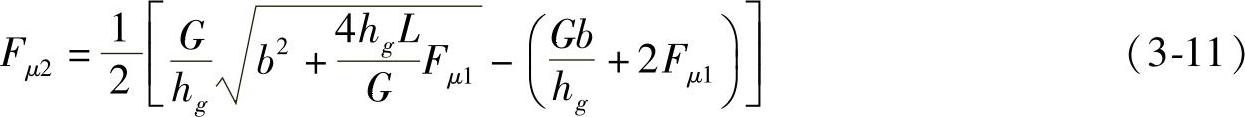
3.I曲线的绘制(https://www.xing528.com)

由式（3-11）绘成的曲线，即为前、后车轮同时抱死时前、后车轮制动器制动力的关系曲线——理想的前、后制动器制动力分配曲线，简称I曲线。

根据方程组（3-10）的两个方程，一般可用作图法直接求得I曲线，其方法步骤是：

1）用不同的φ值（φ=0.1，0.2，0.3，……）分别代入方程组（3-10）的第一式作图画在图2-37上，便得到一组与坐标轴成45°角的平行线。

2）同样，用不同的φ值（φ=0.1，0.2，0.3，……，1.0）分别代入方程组（3-10）的第二式在同一坐标作图，便得一组通过坐标原点、斜率不同的射线。射线的斜率等于F_Z2/F_Z1，斜率随φ的增大而逐渐减小。

3）在这两组直线中，对于某一φ值，均可找到对应的两线直线，其交点便能同时满足式（3-10）中两式的F_μ1值和F_μ2值。

4）把对应于不同φ值的两直线交点A、B、C、……连接起来，便得到了I曲线，如图3-37所示。曲线上任一点的附着系数，代表在该附着系数路面上前、后制动器制动力应有的数值。

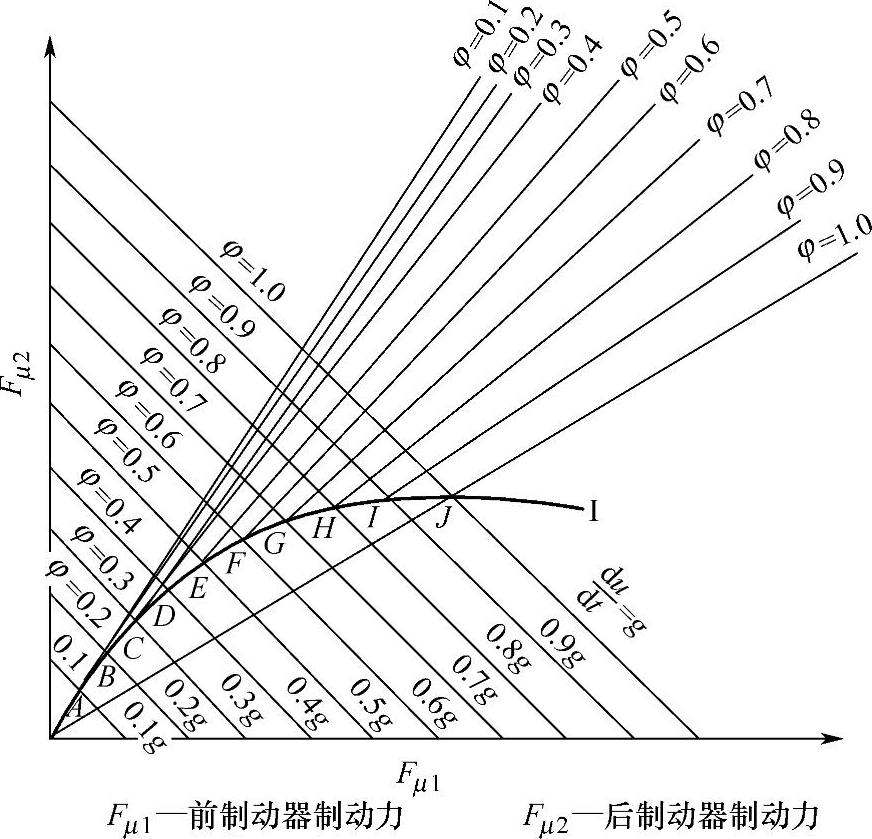
图3-37 理想的前、后制动器制动力分配I曲线

由此可见，只要给出汽车的总质量和汽车的质心位置（a、b和h_g），就能作出I曲线。

对I曲线作以下两点说明：

1）I曲线是制动踏板力增长到前、后车轮同时抱死拖滑时的前、后制动器制动力的分配曲线。车轮同时抱死时，有F_μ1=F_xb1=F_φ1，F_μ2=F_xb2=F_φ2，所以I曲线也是F_φ1和F_φ2的关系曲线。

2）在实际的制动过程中，常是一车轴的车轮先抱死，随着踏板力的进一步增加，接着另一车轴的车轮才抱死。显然，I曲线还是前、后车轮都抱死后的地面制动力F_Xb1与F_Xb2，亦即附着力F_φ1与F_φ2的关系曲线。