汽车工程应用力学：硬路面附着系数为3.2.4

图3-4 制动时轮胎留在地面上的印痕

1.汽车制动时的地面印迹

上一节曾假设车轮的制动过程只有滚动和抱死拖滑这两个极端情况，但实际上车轮的制动过程是一个从滚动到抱死的渐变过程。图3-4为汽车制动过程中逐渐增大踏板力时轮胎留在地面上的印迹，这印迹基本上分为三段。

第一段内，印迹的形状与轮胎胎面花纹基本一致，可以认为车轮还接近于纯滚动，这时

u_w≈r_roω_w

式中 u_w——车轮中心的速度；

r_ro——制动前的车轮滚动半径；

ω_w——车轮的角速度；

r_roω_w——车轮角速度所对应的线速度。

第二段内，轮胎花纹的印迹虽能辨别，但已逐渐模糊；轮胎已不是纯滚动，与地面发生了一定成分的相对滑动，车轮处于边滚边滑的状态，这时

u_w＞r_roω_w

随着踏板力的增加，滑动成分的比例越来越大，印痕越来越模糊，这时

u_w＞＞r_roω_w

第三段的后半部，已经看不出花纹的印痕而形成了一条粗黑的拖印，这表明车轮已被制动器抱住，在路面上进行完全的拖滑，车轮角速度等于零，即

ω_w=0

2.车轮的滑动率

从上一节分析可知，随着制动强度的增加，车轮滚动成分越来越少，滑动成分则越来越多；即车轮中心的速度与车轮角速度所对应的线速度的差值越来越大，直至角速度为零值时完全表现为车轮中心的速度——车轮完全抱死向前拖滑。一般用s来表示在这个过程中滑动成分占了多少比例。因此，滑动率可以定义为

当滑动率s=0时，则表明u_w=r_roω_w，车轮作纯滚动；当滑动率s=100%时，则表明ω_w=0，车轮作纯滑动；当0<s<100%时，则表明车轮处于边滚边滑状态。所以，滑动率值说明了车轮在运动中滑动成分所占的比例。滑动率越大，滑动成分越多。

3.制动过程中附着系数的变化规律

若令地面制动力与垂直载荷之比为制动力系数（即时纵向附着系数），用φ_b表示，即(www.xing528.com)

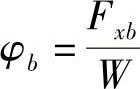
因为在不同的滑动率时，地面制动力F_xb是不同的，所以制动力系数φ_b的数值也跟着变化，φ_b可看成是即时的纵向附着系数。

图3-5绘出了试验所得的制动力系数φ_b曲线，即φ_b-s曲线。实际上，φ_b-s曲线是一条动态的纵向附着系数曲线。从图3-5中可见，曲线在OA段近似于直线，纵向附着系数φ_b随滑动率s几乎成正比（线性）地迅速增大；过A点后φ_b上升缓慢，至B点时φ_b达到最大值，纵向附着系数的最大值称为峰值附着系数φ_p，它一般出现在s=15%～20%时；过B点以后，若滑动率继续增大，纵向附着系数φ_b反而有所下降，直至滑动率为100%，纵向附着系数φ_b则降为一个恒定值φ_s，这个φ_s称为滑动附着系数。在干燥路面上，峰值附着系数φ_p与滑动附着系数φ_s差别较小；但在水湿路面则差别较大，φ_s一般在（1/3～1）φ_p之内变化。

若用地面制动力F_xb来表述以上内容，可表述为：制动时，车轮的滑动率处于OA区间时，其受到的地面制动力呈近乎线性地迅速增大；处于AB区间时，地面制动力上升缓慢，至B点时地面制动力最大，亦即达到了峰值地面制动力；过峰值点B以后，滑动率再增大，地面制动力开始缓慢下降，直至滑动率为100%——轮胎表现为纯滑动时，地面制动力保持一个恒定值，即地面制动力F_xb等于滑动附着力Fφ。试验明确地告诉我们，纯拖滑所获得的地面制动力并不是最大的地面制动力，最大的地面制动力是出现在滑动率为15%～20%的边滚边滑的制动过程中。

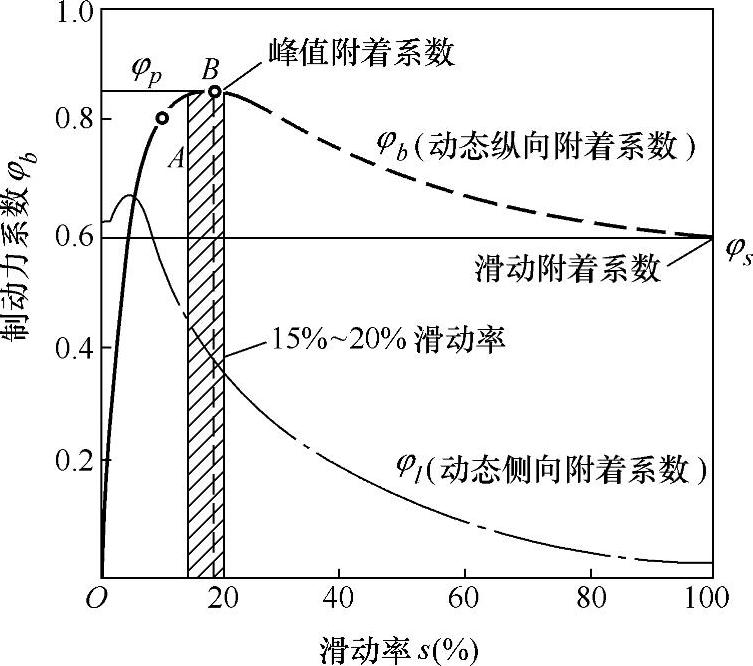
图3-5 制动力系数与滑动率的关系（φ_b-s曲线）

针对图3-5中的φ_b-s曲线，有两个现象需要解释：一是，在OA段虽存在一定的滑动率，但轮胎与地面并没有发生真正的相对滑动。存在这一定的滑动率的原因是由于轮胎滚动半径略微变大的缘故。从上面讨论“滑动率”可知，车轮滚动半径增大则意味车轮中心速度变大，中心速度大于角速度对应的线速度，即u_w=r_rω_w＞r_roω_w，从这个意义上讲，车轮就存在了一定成分的滑动。至于轮胎滚动半径变大是由于受到制动力作用时轮胎即将进入与地接触的那一前面部分胎面受到拉伸所造成的。显然，滚动半径与地面制动力成正比地增大，OA段曲线呈近似直线。二是，B点过后，为什么制动力系数φ_b逐渐降低？A点过后，轮胎接地印迹中出现局部的真正相对滑动，φ_b值的增大速度减慢，因为摩擦副间（胎地间）的动摩擦因数小于静摩擦因数。过峰值点B后，摩擦副间相对滑动率逐渐增大，所以φ_b值逐渐降低。

在制动过程中，路面与轮胎间的附着系数主要取决于道路的材料、路面的状况、轮胎结构、胎面花纹以及汽车的运动速度等因素。表3-2是各种路面的平均附着系数。

表3-2 各种路面上的平均附着系数

4.最佳的制动滑动率

在上一节，我们令地面制动力与垂直载荷之比为制动力系数φ_b；在此，我们令侧向力与垂直载荷之比为侧向力系数φ_l，同理，在不同的滑动率时，φ_l的数值也是不同的。

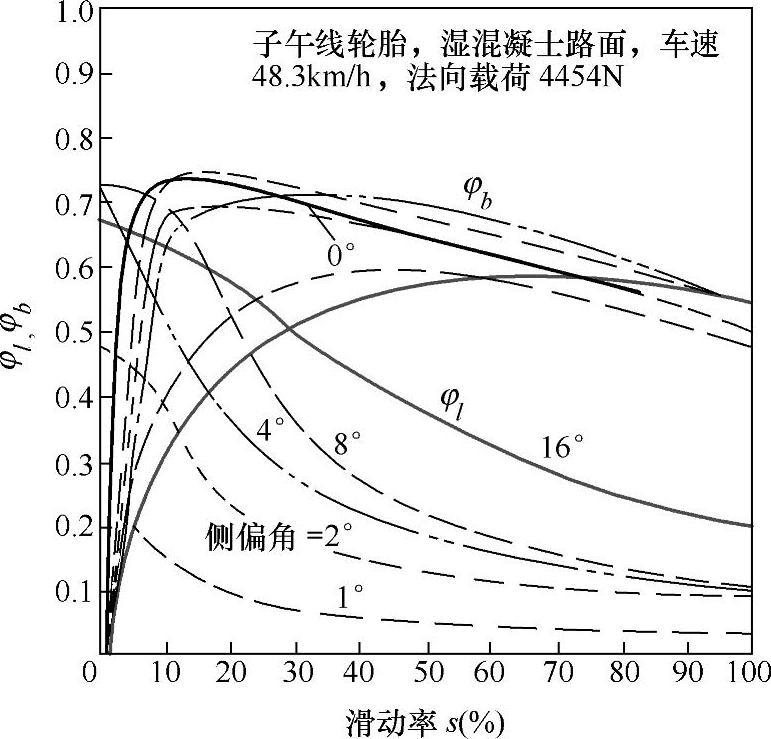
图3-6 轮胎存在侧偏时的φ_b-s、φ_l-s曲线

图3-5的φ_b-s曲线是在轮胎没有受到侧向力的条件下测得的。但在实际行驶的制动中，轮胎常常因受到侧向力的作用而伴随着侧偏或者侧滑，图3-6就是在轮胎产生侧偏的条件下通过试验测得的制动力系数φ_b、侧向力系数φ_l与滑动率s之间的关系曲线。测试的条件为：装用子午线轮胎，在水湿的混凝土路面上，车速为48.3km/h，法向载荷为4454N。图中，除了给出侧偏角为0°值时制动力系数随滑动率变化的曲线以外，还给出了侧偏角分别为1°、2°、4°、8°、16°时制动力系数φ_b和对应的侧向力系数φ_l随滑动率s变化的5组曲线。从图中，可以读出以下情况：

1）在0°侧偏角的曲线上，峰值附着系数比图3-5的数值略有下降，大约只有0.75；滑动附着系数下降得较多，大约只有0.5。其原因是路面水湿影响的缘故。

2）在轮胎有侧偏角的各组曲线上，在较低的滑动率范围内车轮都同时具有较高的制动力系数和侧向力系数。

3）在同一侧偏角条件下，滑动率越低，侧向力系数就越大，亦即轮胎保持转向的能力和防止侧滑的能力就越强。

所以，在实施强制动时，若能使滑动率保持在较低数值，例如s≈15%，便可同时获得较大的纵向制动力系数和较大的侧向力系数。这样，制动效果最好，侧向稳定性也很有保障。

以往，在没有制动防抱装置（ABS）的条件下，有经验的驾驶人通常采用对制动踏板连续施于“一踩一松”的点制动方法来获得较高的制动效果，尤其是在下长坡时。现代轿车基本都装用电控的制动防抱死装置（ABS），便可自动做到这一点，从而显著地改善了汽车的制动效能和制动时的方向稳定性。