计算土方工程量的基本方法

1.3.3.1 三棱柱法

计算时先把方格网顺地形等高线将各个方格划分成三角形（图1.11）。每个三角形的3个角点的填挖施工高用h1、h2、h3表示。

（1）当三角形3个角点全部为挖或填时，如图1.12（a）所示，其挖填方体积为

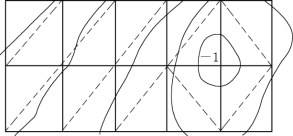
图1.11　按地形方格划分成三角形

式中　a——方格边长，m；

h1、h2、h3——三角形各角点的施工高度，用绝对值代入，m。

（2）三角形3个角点有挖有填时，零线将三角形分成两部分：一个是底面为三角形的锥体，另一个是底面为四边形的楔体，如图1.12（b）所示。

其锥体部分的体积为

式中 h1、h2、h3——三角形各角点的施工高度，取绝对值，h3 指的是锥体顶点的施工高度，m。

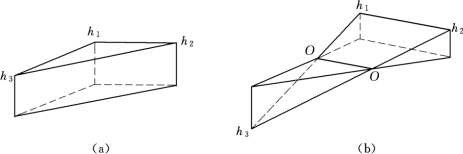
图1.12　三角棱柱体的体积计算

（a）全挖或全填；（b）锥体部分为填方

1.3.3.2 四棱柱法

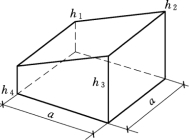
（1）方格4个角点全部为挖或填方时（图1.13），其挖方或填方体积为

式中 h1、h2、h3、h4——方格生个角点挖或填的施工高度，以绝对值代入，m；

a——方格边长，m。

（2）方格4个角点中，部分是挖方，部分是填方时（图1.14），其挖方或填方体积分别为

(www.xing528.com)

图1.13　角点全填或全挖

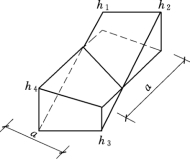
图1.14　角点二填或二挖

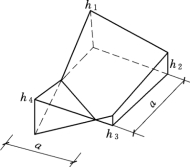
图1.15　角点一填三挖

（3）方格3个角点为挖方，另一个角点为填方时（图1.15），其填方体积为

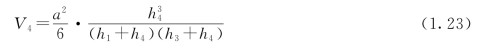
其挖方体积为

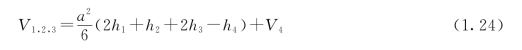
1.3.3.3 断面法

在地形起伏变化较大的地区，或挖填深度较大，断面又不规则的地区，采用断面法比较方便。

方法：沿场地取若干个相互平行的断面（可利用地形图定出或实地测量定出），将所取的每个断面（包括边坡断面），划分为若干个三角形和梯形，见图1.16，则面积为

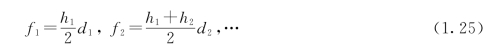
某一断面面积为

若d1=d2=…=dn=d，则

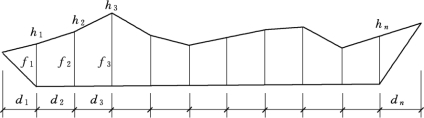
图1.16　断面法

断面面积求出后，即可计算土方体积，设各断面面积分别为：F1、F2、…、Fn，相邻两断面间的距离依次为：L1、L2、L3、…、Ln，则所求土方体积为

用断面法计算土方量时，边坡土方量已包括在内。值得注意的是，四方棱柱体的计算公式是根据平均中断面的近似公式推导而得的，当方格中地形不平时，误差较大，但计算简单，宜于手工计算。三角棱柱体的计算公式是根据立体几何体积计算公式推导出来的，当三角形顺着等高线进行划分时，精确度较高，但计算繁杂，适宜用计算机计算。