某一公交线路总站点数N=19，车辆0、车辆1和车辆2之间的发车间隔分别为6.2min和3.7min，车辆0在首站处发车时刻为17：00：00。各站点处乘客平均到达率为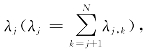
如表10-1所示。
表10-1 各站点处乘客平均到达率（单位：人/min）
假设在站点j上车的乘客在站点j后面的各个站点处下车的概率是相同的，得到各个
取值（单位：人/min），分别为
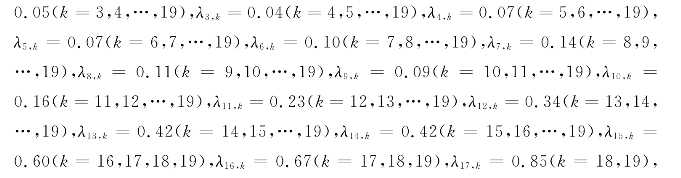
绘制出各站点处的上、下客情况，如图10-3所示。
图10-3 各站点处上、下客情况
每个乘客上车平均所需时间B=0.07 min，下车平均所需时间A=0.03 min，公交车辆在站点处的加速和减速总时间δ=0.3 min，临界车头时距H0=0.15 min。
假设不同公交车辆在站点j-1和站点j之间的行驶时间服从同一分布，并假设站点间行驶时间服从正态分布，即
。rj和σj分别为站点j-1和站点j之间车辆随机行驶时间Tj的均值和标准差。具体的各站点间平均行驶时间rj（单位：min）分别为：r2=5.0，r3=0.98，r4=1.72，r5=2.59，r6=3.24，r7=1.57，r8=3.49，r9=1.02，r10=2.19，r11=2.40，r12=3.83，r13=3.30，r14=2.52，r15=2.78，r16=3.43，r17=3.55，r18=1.01，r19=2.80。令各站点间行驶时间的变异系数为0.2，即σj=0.2rj。车辆0在各站点处的离站时刻为初始条件，列于表10-2。
令各权重系数值C1=1，C2=1，C3=1，惩罚参数M=108。
表10-2 车辆0在各站点处的离站时刻
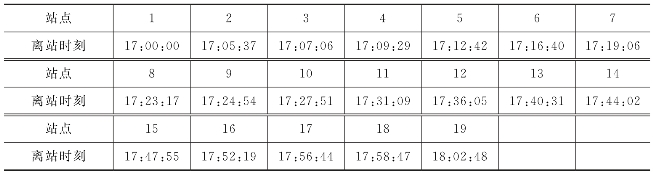
采用包含蒙特卡罗仿真的遗传算法进行求解，交叉率ρc和变异率ρm分别为0.25和0.01。令种群规模为100，种群最大代数为60，蒙特卡罗抽样规模设为60。
以无调度控制策略（即不允许越站）情况下的计算结果作为参照标准，此时目标函数值z=4 523 min，其中z1=956 min，z2=3 446 min，z3=121 min。(www.xing528.com)
表10-3给出了车辆1的最优中途越站调度控制方案，即在站点17和站点18处越站，对应的目标函数值z=3 656 min，其中z1=399 min，z2=3 140 min，z3=117 min。与无调度控制策略情况相比，中途越站有效改善了公交运行，总成本降低了19%。
表10-3 车辆1最优越站方案：站点间行驶时间服从正态分布
为了检验含蒙特卡罗仿真的遗传算法的计算性能，采用枚举算法计算全局最优解，由于站点1和站点19不允许越站，中途越站调度控制方案共有217=131072种可能。对所有的方案进行枚举并采用蒙特卡罗过程计算目标函数值，得到目标函数值的最小值z=3 656 min，对应的越站方案与表10-3中相同，最大值为1.680×106min，均值为1.633×106min。由于惩罚参数的设置，与最小值相比，最大值和均值量级均较大，可知遗传算法可以快速获取枚举算法所能计算得到的全局最优解，说明算法可行且高效。
继续求解当各站点间行驶时间为常量时的情况，分析随机行驶时间对越站方案的影响。同样采用遗传算法进行求解，此时不再需要蒙特卡罗抽样过程。表10-4给出了各站点间行驶时间为常量（即σj=0）时车辆1的最优中途越站调度控制方案，与各站点间行驶时间服从正态分布时获取的方案有所不同，此时目标函数值z=3 771 min，其中z1=371 min，z2=3 284 min，z3=116 min。可见行驶时间的随机性影响了最优越站方案，在应用调度控制策略时应将公交车辆运行随机性考虑在内。
表10-4 车辆1最优越站方案：站点间行驶时间为常量
同样采用枚举算法计算各站点间行驶时间为常量的情况，目标函数的最小值z=3 683 min，其中z1=349 min，z2=3 218 min，z3=116 min。对应的越站方案如表10-5所示，最大值为1.683×106min，均值为1.667×106min。可见含蒙特卡罗仿真的遗传算法获取的解的质量较好。
表10-5 车辆1最优越站方案：站点间行驶时间为常量（枚举算法）
如10.2.2节中所述，考虑到实际情况或调度控制人员的偏好，可以增加其他的约束条件，如不允许连续越站等，采用含蒙特卡罗的遗传算法进行求解。表10-6为不允许连续越站情况下车辆1的最优中途越站调度控制方案，即在站点16和站点18处越站。目标函数值为z=3 706 min，其中z1=408 min，z2=3 181 min，z3=117 min。
表10-6 车辆1最优越站方案：不允许连续越站
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
