城市公交协调案例应用及有效性验证

以图9-5所示新加坡轨道交通网络为例验证末班列车运行计划优化方法的有效性。线路基本属性参见表9-4。每条轨道交通线路沿线所途经的换乘站点情况见表9-5。轨道交通线路末班列车现状运行计划参见表9-13。

乘客往往乘坐末班列车从市中心或市郊工业园区返回市郊居住区。连接上述地区的线路及其内部关键换乘关系为本案例中需要优化的关键换乘关系。通过分析，从轨道交通网路中识别筛选出27对关键换乘关系，具体参见表9-14。同时这27对换乘关系现状末班列车换乘情况也已在表9-14中列出。

研究时间范围内从轨道交通线路计划从首站发出的班次的数量设为21，计划发车间隔参见表9-13。参数和分别设为23：10和00：20。换乘站点内线路间换乘步行时间统一设为3 min。末班列车行驶速度最高增大和减小幅度分别为1.25和0.80。末班列车计划停靠时间最高增大和减小幅度分别为1.20和0.80。根据公式（9-35）和（9-75），目标函数中权重δ、σ和φ的取值分别为0.05、0.05和0.20。采用YALMIP语言[203]在MATLAB（R2013a）平台编写求解程序，并调用CPLEX12.6获取最优解。具体计算过程在一台内存为16G的台式机（Intel Core i7-2600 CPU@3.40GHz）上完成。

表9-13　末班列车现状运行计划（单位：min）

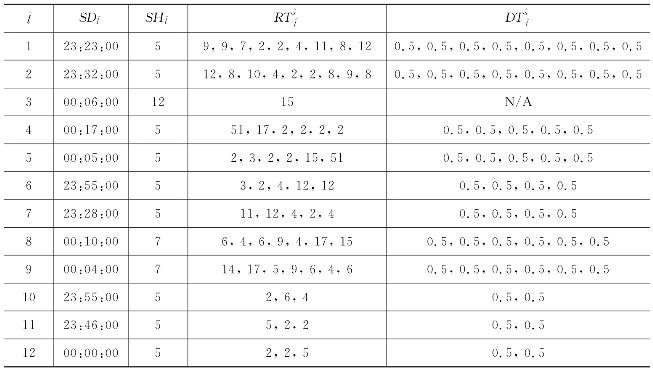
表9-14　末班列车现状换乘情况

续表9-14

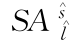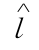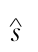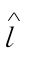注：表示线路末班列车在换乘站点处的现状计划到站时刻表示线路末班列车在换乘站点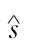处的现状计划离站时刻。

1.案例结果分析

表9-15列出了由所建模型产生的末班列车运行计划最优调整方案。通过与表9-13中的现状运行计划相比，发现优化后轨道交通线路1、线路2、线路5、线路7、线路8、线路10和线路11的末班列车首站计划发车时刻被延后了；轨道交通线路4和线路9的末班列车首站计划发车时刻被提前了；而轨道交通线路3和线路12的末班列车首站计划发车时刻保持不变。另外，轨道交通线路1、线路4和线路6的末班列车首站计划发车时刻达到极值（即23：10和00：20）后，仍需要调整其末班列车的计划运行时间。事实上，轨道交通线路4和线路6的末班列车在换乘站点处的计划停靠时间也进行了适当调整以减少换乘失败。

以轨道交通线路4为例具体说明整个调整过程。当线路4的末班列车首站计划发车时刻被提前至23：10且计划运行时间减小幅度达到极值后，将于00：11：12到达滨海湾站；然而轨道交通线路10的末班列车在滨海湾站的离站时刻为00：13：48，则线路4的末班列车计划停靠时间必须缩短至少24 s（即0.4 min），列车上的乘客方能顺利在滨海湾站换乘至线路10的末班列车。

表9-15　末班列车运行计划最优调整方案（单位：min）(www.xing528.com)

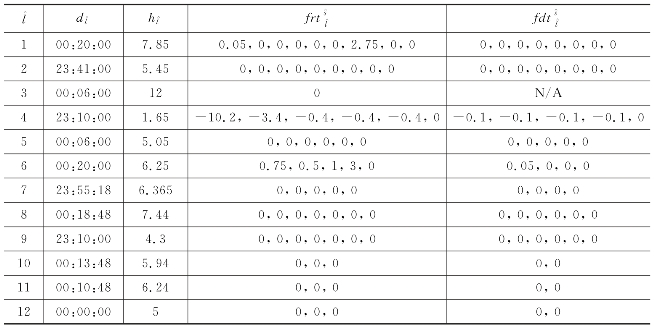
表9-16列出了末班列车运行计划优化后每个关键换乘关系的换乘情况。与表9-14中展示的换乘情况相比，可知27对关键换乘关系内换乘成功的关系由6对增加为24对。也就是说线路间末班列车换乘情况可得到大幅度改善。而且可以发现协调后发车间隔的变化较小，意味着运营者不需要调整车辆和人员调度安排。即在给定的资源下，所构建模型可被运营调度人员作为有效的辅助分析工具帮助其调整现状运行计划以大幅度地提高整个轨道交通网络的换乘衔接性。

表9-16　协调后末班列车换乘情况

续表9-16

2.权重赋值方法有效性验证

为了验证9.2.2节所介绍的权重赋值方法的有效性，在所构建的混合整数线性规划模型中令目标函数的权重δ=σ=φ=0，其他参数设置不变。表9-17给出了协调后各换乘关系的换乘情况。由CPLEX求解所得末班列车运行计划最优调整方案可见表9-18。

表9-17和表9-16的比较说明当δ=σ=φ=0时，27对换乘关系中换乘成功的关系保持不变，意味着9.2.2节提出的权重赋值方法确实能消除权重取值对模型最终优化结果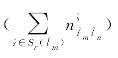的影响。表9-18与表9-15的比较也表明借助合适的权重取值，调整策略实施顺序的约束（9-33）和（9-34）能够切实发挥积极作用。

表9-17　协调后末班列车换乘情况当（δ=σ=φ=0）

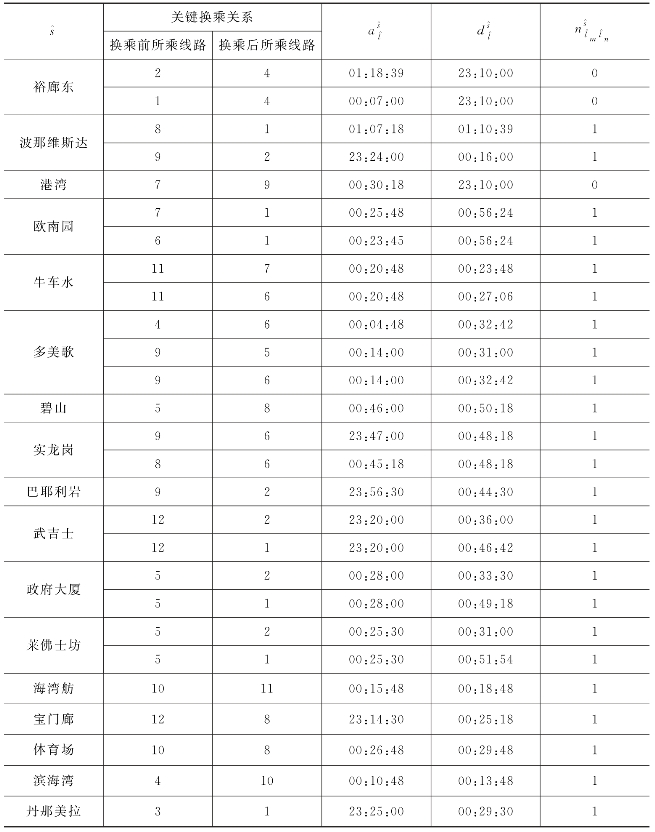
表9-18　末班列车运行计划最优调整方案（当δ=σ=φ=0）（单位：min）