末班列车运行计划方法

在构建面向末班列车换乘问题的轨道交通运行计划协调优化模型前，需要先明确可用于调整现状列车运行计划的具体协调策略。需要注意的是所构建的优化模型旨在通过适当调整研究时间范围内（即深夜时段，约22：00至24：00）现状运行计划以减少换乘失败情况，而非重新制订一份覆盖全天的完整的列车运行计划。

1.面向换乘的列车运行计划协调策略

列车运行计划协调优化策略必须易在实际调度中实现，以增强协调优化模型的可行性和实用性。

策略1：如果轨道交通线路末班列车在目标换乘站点存在换乘失败情况（即当乘客到达换乘站点时所需换乘线路上的末班列车已离站），则首先对研究时间范围内的列车运行计划进行整体偏移。

假定研究时间范围内轨道交通线路以均匀的发车间隔从首站发出班列车，则运行计划的整体偏移可通过统一偏移最后班列车的首站计划发车时刻实现。偏移后最后班列车间的计划发车间隔和协调后的线路上末班列车首站计划发车时刻满足以下关系：

式中——协调后线路末班列车首站计划发车时刻；

——协调后研究时间范围内线路计划发车间隔（min）；

——线路末班列车现状首站计划发车时刻；

——研究时间范围内线路现状计划发车间隔（min）。

式中——所允许的末班列车最早首站计划发车时刻；

——所允许的末班列车最晚首站计划发车时刻。

公式（9-21）表明倒数第班列车及其之前的所有列车的首站计划发车时刻固定不变，即不会被调整。正如前文所述，模型旨在微调研究时间范围内现状运行计划而非重新设计完整列车运行计划。举例说明，将晚上10点至半夜的时段设定为研究时间范围，假定此时段内列车发车间隔为10 min左右，则约有11班列车的首站计划发车时刻会有所调整。公式（9-22）则表明调整后的末班列车首站计划发车时刻必须在预先给定的时间范围内取值。

策略2：当研究时间范围内运行计划整体偏移后目标换乘站点仍存在换乘失败情况时，可考虑适度调整末班列车计划运行时间。

列车可通过适当加、减速以调节各区段间运行时间。调整后末班列车在换乘站点至换乘站点之间区段的计划运行时间可按式（9-23）计算获取。

式 中——协调后线路末班列车在换乘站点和换乘站点之间区段的计划运行时间（min），包括区段内中间站点处列车计划停靠时间；

——现状线路末班列车在换乘站点和换乘站点之间区段的计划运行时间（min）；

——末班列车在换乘站点至换乘站点之间区段的计划运行时间的调整幅度（min）。

考虑到运输安全要求，建议调整后末班列车行驶速度不得大于现状行驶速度的λinc倍；同时考虑到运输效率要求，建议调整后末班列车行驶速度不得小于现状行驶速度的λdec倍。故末班列车在换乘站点至换乘站点之间区段的计划运行时间的调整幅度应满足约束条件（9-24）。

式中：λinc——末班列车行驶速度最高增大幅度，λinc≥1；

λdec——末班列车行驶速度最高减小幅度，0＜λdec≤1。

当λinc=λdec=1时，末班列车在换乘站点至换乘站点之间区段的计划运行时间不允许被调整。

策略3：末班列车在换乘站点处的计划停靠时间也可在适当范围内微调以最大限度地减少线路间换乘失败情况。

调整后轨道交通线路上末班列车在换乘站点处计划停靠时间为现状计划停靠时间与调整幅度之和，具体可参见式（9-25）和（9-26）。

式 中——协调后线路末班列车在换乘站点处的计划停靠时间（min）；

——现状线路末班列车在换乘站点处的计划停靠时间（min）；

——线路末班列车在换乘站点处计划停靠时间的调整幅度（min）。

式中：ρinc——末班列车计划停靠时间最高增大幅度，ρinc≥1；

ρdec——末班列车计划停靠时间最高减小幅度，0＜ρdec≤1。

如式（9-26）所示，考虑到运输效率要求，建议调整后的末班列车计划停靠时间不得大于现状计划停靠时间的ρinc倍；同时考虑到列车上下客时间要求，建议调整后末班列车计划停靠时间不得小于现状计划停靠时间的ρdec倍。具体应用时，参数ρinc和ρdec的取值可结合实际情况灵活调整，例如当ρinc=ρdec=1时，则末班列车在换乘站点处的计划停靠时间不允许被调整。

2.优化模型

当线路末班列车在换乘站点处的计划到站时刻比线路末班列车在换乘站点处的计划离站时刻能提前从线路换乘至线路所需步行时间时，线路末班列车上的乘客才能顺利在换乘站点处换乘至线路因此，定义二元变量表征线路末班列车上的乘客是否可以顺利在站点换乘至线路具体参见式（9-27）和（9-28）。

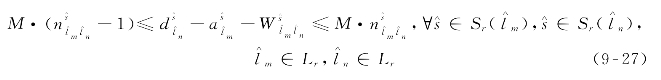
式中：M——一个足够大的已知正数；

——二元变量：当线路末班列车上的乘客能顺利在站点换乘至线路时，等于1，否则等于0；

——协调后线路末班列车在换乘站点处计划离站时刻；

——换乘站点处从线路至线路的平均步行时间（min）。

以图9-6为例，情景1和2线路末班列车上的乘客能顺利在换乘站点处换乘至线路而情景3和4线路末班列车上的乘客将面临换乘失败的窘境。

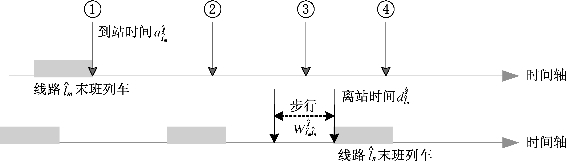
图9-6　换乘示意图

如式（9-29）所示，线路末班列车在换乘站点处计划到站时刻由列车首站计划发车时刻从首站至换乘站点区段内计划运行时间之和、从首站至换乘站点区段内换乘站点处计划停靠时间之和共同决定。相应地，线路末班列车在换乘站点处计划离站时刻可按式（9-30）计算。

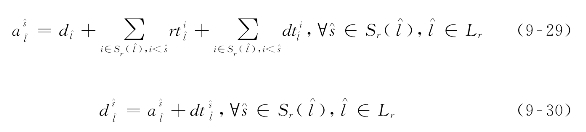
末班列车首站计划发车时刻偏移量则可按式（9-31）计算。

式中：——线路末班列车首站计划发车时刻的偏移量（min）。(www.xing528.com)

合理的末班列车运行计划协调优化方案应不仅能使成功完成换乘的关键换乘关系数量（即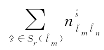）最大，同时也能使首站计划发车时刻偏移量（即）、计划运行时间调整幅度（即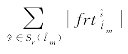）和计划停靠时间调整幅度（即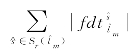）最小。故构建目标函数（9-32）以同时响应上述诉求。

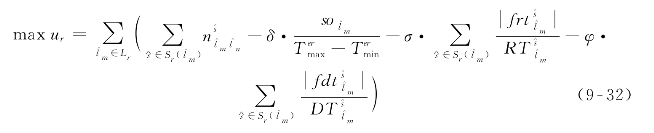
式中：ur——目标函数值；

δ——非负权重系数，反映减少首站计划发车时刻偏移量的重要性；

σ——非负权重系数，反映减少计划运行时间调整量的重要性；

φ——非负权重系数，反映减少计划停靠时间调整量的重要性。

由于非负权重δ、σ和φ的作用使得当所有调整策略都尝试过后，若末班列车间能成功换乘的关键换乘关系数量也无法提高时，则放弃对现状运行计划的调整。这与构建面向末班列车换乘问题的运行计划协调优化模型的初衷相一致，即主要是为了减少换乘失败的换乘关系，而非其他目标（如减少换乘等待时间）。

考虑到调整策略对象的差异及其对列车运行影响程度的不同，在构建优化模型时，推荐按照以下顺序逐步实施上述换乘协调策略：首先考虑整体偏移研究时间范围内运行计划（策略1），然后考虑微调末班列车区段计划运行时间（策略2），最后再考虑调整末班列车在换乘站点处的计划停靠时间（策略3）。具体来说，只有当末班列车首站计划发车时刻被调整至极值时末班列车在区段内的计划运行时间方可在预定的取值范围内波动；而只有当所有可行的计划运行时间调整方案都采用了之后才能微调末班列车在换乘站点处的计划停靠时间。故提出式（9-33）～（9-36），联合式（9-32）以控制协调策略实施的先后顺序。

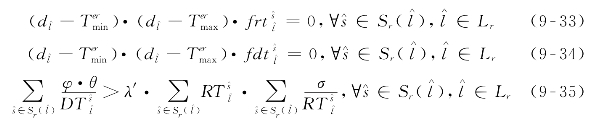
式中：θ——辅助参数，表示以分钟为单位的1个单位时间（即1 min），用以保证不等式（9-35）两侧度量单位一致。

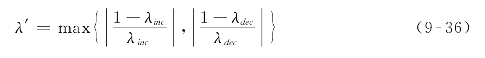
根据式（9-33）和式（9-34），当时，变 量和必须等于零。根据式（9-32）、式（9-35）和式（9-36），调整1个单位的计划停靠时间的惩罚（即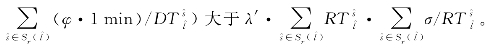事实上，式（9-24）和

式（9-36）表明是当末班列车首站计划发车时刻达到极值后其区段计划运行时间可实现的最大调整幅度。故计划运行时间调整策略必然会在实施计划停靠时间微调策略前执行。需要注意的是目标函数中的权重φ和σ是由运营者根据式（9-35）和式（9-75）预先确定的常数。

综上所述，协调优化后末班列车最优运行方案可通过求解以下混合整数非线性规划模型获取。具体需要求解的决策变量包括：协调后末班列车首站计划发车时刻、各区段内计划运行时间调整幅度和各换乘站点处计划停靠时间调整幅度。

目标函数：式（9-32）

约束条件：基本约束：式（9-21）～式（9-31）

顺序约束：式（9-33）～式（9-34）

混合整数非线性规划模型很难求解获取其全局最优解，幸而上述所构建模型可以等价转化为混合整数线性规划模型。通过引入非负辅助变量和式（9-31）中的绝对值表达式可线性化为式（9-39）。

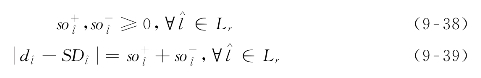
通过引入非负辅助变量和，式（9-32）中绝对值表达式可线性化为式（9-42）。

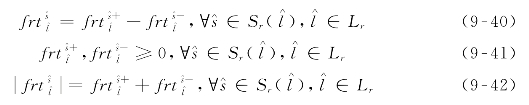
类似地，式（9-32）中绝对值表达式可通过引入非负辅助变量和线性化为式（9-45）。

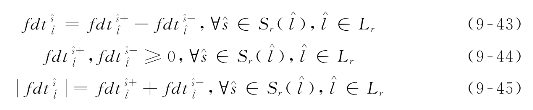
目标函数表达式（9-32）相应更新为

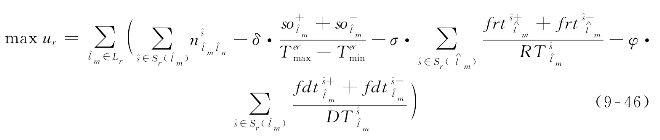
约束条件（9-56）～（9-67）联合式（9-47）～（9-55）可将关于策略实施顺序的约束条件（9-33）～（9-34）转化为线性约束。其中，需要引入非负辅助变量和以及二元辅助变量和

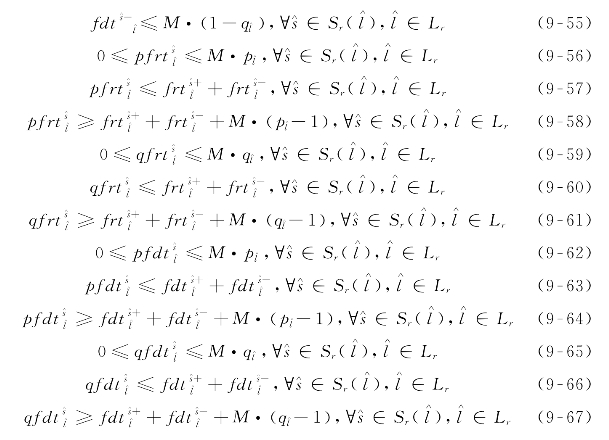
相应地，公式（9-23）和（9-25）需分别更新为式（9-68）和（9-69）。

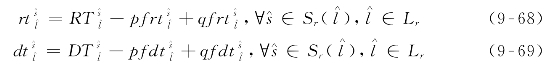
本质上，约束条件（9-47）～（9-69）可实现：

当（即）时，且即末班列车的计划运行时间和计划停靠时间都不会被调整。

当（即且）时，且，即末班列车计划运行时间和计划停靠时间可适当缩短以减少换乘失败情况。

当（即且）时，即末班列车计划运行时间和计划停靠时间可适当延长以减少换乘失败情况。

综上可知，运行计划协调优化策略及其实施顺序确实可以作为线性约束条件纳入优化模型，即混合整数非线性规划模型的确可借助辅助变量和不等式约束转化为以下等价的混合整数线性规划模型：

目标函数：式（9-46）

约束条件：基本约束：式（9-21）、（9-22）、（9-68）、（9-24）、（9-69）、（9-26）～（9-30）、（9-37）、（9-38）、（9-40）、（9-41）、（9-43）、（9-44）顺序约束：式（9-47）～（9-67）

可利用分支定界法求解上述混合整数线性规划模型，便捷地获取模型精确解。

3.权重赋值方法

根据前文的阐述可知权重σ和φ的取值必须满足公式（9-35）所表达的关系式；同时权重δ、σ和φ的取值必须保证不影响末班列车运行计划协调优化模型最终结果。即当δ=σ=φ=0时，优化后换乘成功的换乘关系保持不变。

基于前文的分析，易得

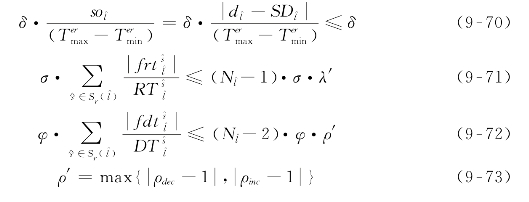
式中——轨道交通线路沿线换乘站点数（个），包括存在换乘关系的首末站。

因此，对于每一条待协调的轨道交通线路应满足

其中不等式右边的表达式定义为运行计划调整最高“惩罚”。

根据公式（9-32）和（9-74），若可以保证增加一对能换乘成功的换乘关系的“利益”总是大于运行计划调整最高“惩罚”，则任何可能成功的换乘关系都可通过适当的末班列车运行计划调整方案实现。也就是说，对于任一待协调的轨道交通线路，目标函数中权重的取值必须满足以下要求：

因此，对于目标函数中权重的取值必须由公式（9-35）和（9-75）共同决定。故在不同的轨道交通网络内应用优化模型时，其权重的取值往往有所差别。