多模式公交首班车运行计划方法

1.基础模型

根据轨道交通线路区段计划运行时间、站点处停靠时间及其优化后首班列车计划发车时刻，可推导出优化后线路首班列车于轨道站处计划到站时刻，如（9-1）所示。

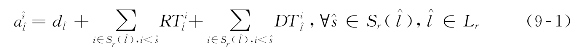
式 中—优化后轨道交通线路首班列车于轨道站处计划到站时刻；

——优化后轨道交通线路首班列车计划发车时刻；

—轨道交通线路在轨道站和轨道站之间区段的计划运行时间（min）；

——轨道交通线路在轨道站处的计划停靠时间（min）。

优化后线路首班列车于轨道站处的计划离站时刻为首班列车于轨道站处的计划到站时刻与计划停靠时间之和，如式（9-2）所示。

式中—优化后轨道交通线路首班列车于轨道站处计划离站时刻。

轨道交通线路运行计划在不过度增加企业运营成本的前提下应最大限度地满足居民出行需求，故线路首班列车于各轨道站处计划离站时刻被要求限定在一定时间区间内，即

式中——所允许的首班列车于各轨道站点处的最早计划离站时刻；

——所允许的首班列车于各轨道站点处的最晚计划离站时刻。

所允许的首班列车于各轨道站点处的最早计划离站时刻和最晚计划离站时刻为运行计划优化模型中两个重要参数，由轨道交通运营企业和政府管理部门协商确定。

首班列车计划发车时刻即为首班列车于首站处计划离站时刻，故

基于各线路首班列车于各轨道站点处的计划到站时刻、离站时刻，即可推算出在轨道站处线路首班列车与线路首班列车间换乘衔接时间，即

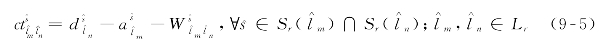
式 中——轨道站处轨道交通线路首班列车乘客换乘至轨道交通线路首班列车时换乘衔接时间（min）；

——优化后轨道交通线路首班列车于轨道站处计划离站时刻；

——优化后轨道交通线路首班列车于轨道站处计划到站时刻；

——轨道站处乘客从线路步行至线路平均所需时间（min）。

由式（9-5）易知，换乘衔接时间的取值可能为正数（如图9-1所示），可能等于零（如图9-2所示），也可能为负数（如图9-3所示）。假设轨道交通列车载客能力总能满足换乘需求，即换乘乘客总能顺利乘坐其到站后最先到站的列车离开，该假设与非客流高峰期实际情况相符。

图9-1　换乘衔接时间取正值情景示意图

图9-2　换乘衔接时间取零值情景示意图

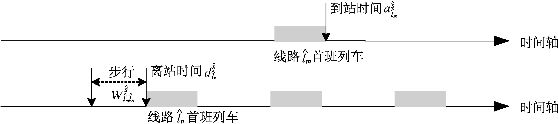
图9-3　换乘衔接时间取负值情景示意图

当取值为非负数时，说明线路首班列车上乘客可以顺利在轨道站处乘坐线路首班列车离开，即此时换乘衔接时间即为乘客实际的换乘等待时间，如式（9-6）所示：

式中：——轨道站处轨道交通线路首班列车乘客换乘至轨道交通线路时的换乘等待时间（min）。

反之，当取值为负数时，意味着线路首班列车上乘客在轨道站处无法赶上线路首班列车，而将乘坐其到站后线路最先到达轨道站的列车（可能是线路的第二班列车、第三班列车……）离开，此时换乘衔接时间与乘客实际的换乘等待时间满足以下关系式：

式 中：——轨道站处轨道交通线路首班列车乘客顺利换乘至轨道交通线路后所乘列车与线路首班列车间相差班次数（班）；

——研究时间范围内轨道交通线路计划发车间隔（min）。

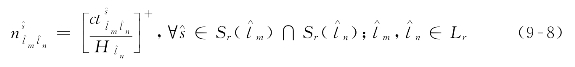
式中：[]+——向上取整操作。

式（9-8）用以确保轨道交通线路首班列车乘客所乘列车为其到站后最先到达轨道站的来自线路的列车。

为统一两种情况下换乘衔接时间与换乘等待时间的关系式，增加辅助二元变量如式（9-9）和（9-10）所示。当轨道交通线路首班列车于轨道站处的计划到站时刻比轨道交通线路首班列车于轨道站处的计划离站时刻至少提前乘客从线路步行至线路所需时间时（即当≥0时）等于1，否则等于0。

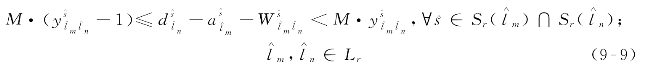
式中：M——一个足够大的已知正数。(www.xing528.com)

此时，上述两种不同情况下换乘衔接时间与换乘等待时间的关系式可统一表达成：

合理的轨道交通首班列车运行计划应尽可能减少乘客的换乘等待时间，故将首班列车运行计划优化模型的目标函数定义为：

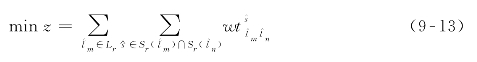
式中：z——目标函数值，即网络内总换乘等待时间（min）。

考虑到模型优化目标为使总换乘等待时间最小化，用线性约束条件（9-14）～（9-16）替代非线性约束条件（9-11）和约束条件（9-12）。

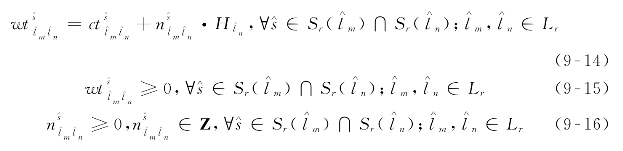
式中：Z——整数集合。

式（9-15）和（9-16）分别给出了变量和合理的取值范围。基于目标函数（9-13），约束条件（9-14）～（9-16）可实现：当时等于0；当时等　于 使的最小正整数。即结合目标函数（9-13），利用约束条件（9-14）～（9-16）可准确识别与线路首班列车具有换乘关系的来自线路的车次，并计算乘客相应的换乘等待时间。

综上可知，轨道交通首班列车运行计划优化问题可抽象为以下数学模型：

目标函数：式（9-13）

约束条件：式（9-1）～（9-5）、（9-14）～（9-16）

上述所构建的优化模型为混合整数线性规划模型，可利用分支定界法精确求解，即调用包含分支定界法的整数规划求解器如CPLEX便可便捷地获取模型精确解。

2.考虑换乘关系重要度

在上文所构建的优化模型中，目标函数（9-13）以各目标换乘站处目标换乘关系对应换乘等待时间总和最小为优化对象，未考虑换乘关系重要度差异，将在一定程度上影响优化方案的实际应用效果。如能在模型中充分结合实际情况优先满足具有高重要度的换乘关系将使得最终的首班列车运行计划优化方案能更好地响应实际诉求。

轨道交通网络内换乘关系重要度确定方法可采用（但不限于）以下两种思路：

（1）根据换乘客流量确定重要度

以历史客流需求，即线路首班列车于轨道站处换乘线路的历史客流量，衡量各换乘关系的重要度，将目标函数（9-13）更新为

式中：——线路首班列车于轨道站处换乘线路的客流量（人）。

由于乘客利用轨道交通完成出行时仅需在进站、出站时各刷卡一次，即由刷卡记录仅可直接读取乘客出行起讫信息（O-D信息），而其在轨道交通网络内的具体出行路径无法直接由刷卡数据获取。但可通过在网络内进行客流分配估计乘客出行路径，继而获取各换乘站点处的换乘客流量。因此，尽管参数的获取工作存在一定难度，但仍具可操作性。

（2）根据网络拓扑结构确定重要度

以目标换乘关系涉及的换乘线路、换乘站点在整个轨道交通网络内的重要性衡量目标换乘关系的重要度。相较于上述介绍的根据客流量确定重要度的方法，根据网络拓扑结构确定重要度的方法更具可操作性。

线路的重要度由以下四要素综合决定：（1）沿线换乘站数量；（2）与其存在换乘关系的线路数量；（3）沿线非换乘站数量；（4）线路长度。根据实际轨道交通网络布局方案确定上述四要素对应参数的取值后，可采用式（9-18）计算线路的重要度。

式中——轨道交通线路的重要度；

——轨道交通线路沿线换乘站数量（个）；

——与轨道交通线路有换乘关系的轨道交通线路数量（条）；

——轨道交通线路沿线非换乘站数量（个）；——轨道交通线路的长度（km）；

ε1——非负权重参数（1/个），表征参数

的重要性；

ε2——非负权重参数（1/条），表征参数的重要性；

ε3——非负权重参数（1/个），表征参数的重要性；

ε4——非负权重参数（1/km），表征参数的重要性。

需要说明的是，参数ε1、ε2、ε3、ε4的合理取值可由经验丰富的轨道交通运营管理人员确定，但需保证ε1+ε2+ε3+ε4=1。

轨道站的重要度由其所属线路的重要性决定，采用（9-19）计算其值。

式中——轨道站的重要度；——途经轨道站的轨道交通线路集合。

此时考虑换乘关系重要度差异的目标函数可表达为式（9-20）。

综上所述，考虑换乘关系重要度差异的优化模型仅需将基础模型的目标函数更新为式（9-20），并增加约束条件（9-18）和（9-19）即可，此时模型仍为混合整数线性规划模型，可利用分支定界法获取模型最优解。