城市公交时刻表协调-城市多模式公共交通运行协调方法

对于基于时刻表运行的地面公交线路，运行可靠性可以通过实际运行与计划时刻表之间的契合程度来度量。故将通过对比时间控制点处公交车辆实际到站时刻与计划到站时刻之间的偏差来评价公交运行可靠性。而对于由于换乘引起的不便，则通过计算线路间换乘等待时间来进行衡量，此种做法在既有与协同调度相关的研究[72，105，125]中已得到广泛应用。

1.运行偏差分析

区段实际运行时间为时间控制点s-1处实际到站时刻与时间控制点s处实际到站时刻之间的差值。显然，此时要求所观测到的实际到站时刻是在车辆处于无控制状态，即时刻表内尚未设置松弛时间。

公交线路l车次k在时间控制点s-1至时间控制点s的区段上计划运行时间为该区段的实际运行时间加上该区段的松弛时间，具体计算参见式（8-1）。

式中——公交线路l车次k在时间控制点s-1至时间控制点s的区段上计划运行时间（min）；

——公交线路l车次k从时间控制点s-1至时间控制点s的实际运行时间（min）；

——公交线路l车次k在时间控制点s-1至时间控制点s的区段上的松弛时间（min）；

Ml——公交线路l沿线时间控制点数量（个）；

K（l）——研究时间范围内需要考虑的服务于公交线路l的所有公交车次的集合；

k——隶属于集合K（l）的某一具体的公交车次。

对于两个连续时间控制点之间的区段而言，若计划运行时间分配得太少，会使驾驶员在“追赶”计划到站时刻时产生挫败感，产生潜在的安全问题，如超速、抢信号灯以及对乘客服务态度差等。而计划运行时间分配得过多时，又会导致不必要的冗余运行时间，导致公交车辆和驾驶员资源的低效使用。不准确的计划到站时刻也可能使得乘客错过与其他方式或线路的换乘，引起乘客关于运行可靠性差的抱怨，甚至需要控制中心重新耗费时间修正时刻表。因此，区段间的计划运行时间的设计取值非常重要。

假设公交站点1处（即首站）的到站时刻是给定的，则时间控制点s处的计划到站时刻可按式（8-2）计算。

式中——公交线路l车次k在时间控制点s处的计划到站时刻；

——公交线路l车次k在时间控制点s-1处的计划到站时刻。

为了保证设计的时刻表在实际中易于操作执行，将时间控制点s处的计划到站时刻设置为以分钟为单位的整数变量，如式（8-3）所示。

式中：N*——正整数集合。

对于公交线路l车次k而言，时间控制点s处的运行偏差即为时间控制点s处公交车辆实际到站时刻与计划到站时刻之间的差值，参见式（8-4）。

式中——公交线路l车次k在时间控制点s处的运行偏差（min）；

——公交线路l车次k在时间控制点s处的实际到站时刻。

若公交车辆在时间控制点s-1处早到，驾驶员则会在时间控制点s-1与时间控制点s之间的区段上减速，以便能够按时到达时间控制点s；相应地，若公交车辆在时间控制点s-1处晚到，驾驶员则往往会在时间控制点s-1与时间控制点s之间的区段上加速，以便能够准时到达时间控制点s。这种现象被视作驾驶员的恢复行为。

借鉴Chen等[211]在公交车辆到站时刻预测中关于驾驶员恢复行为的假设，即驾驶员在时间控制点s-1与时间控制点s之间的区段上对运行偏差的纠正与时间控制点s-1处的运行偏差成正比，如式（8-5）所示。

式中——公交线路l车次k上驾驶员在时间控制点s-1至时间控制点s的区段上对运行偏差的纠正量（min）；

——公交线路l车次k上驾驶员在时间控制点s-1至时间控制点s的区段上关于运行偏差的纠正系数；该系数主要取决于区段的长度和道路交通状况，为一个随机变量。

另外，假设驾驶员总能准时到达公交站点1（即首站），令等于0，即第一个区段上不存在驾驶员的恢复行为。

驾驶员调整后时间控制点s-1至时间控制点s的区段上实际运行时间即为相应地，考虑驾驶员恢复行为的时间控制点s处实际到站时刻可按式（8-6）计算。

根据式（8-5）～（8-6），式（8-4）更新为：

根据式（8-1），式（8-7）进一步更新为：

由于假设驾驶员总能准时到达时间控制点1处发车，即时间控制点1处不存在运行偏差，则

采用和两个随机向量分别表示公交线路l车次k在时间控制点s-1至时间控制点s的区段上随机运行时间和随机运行偏差纠正系数。采用表示公交线路l车次k在时间控制点s-1至时间控制点s的区段上的设计松弛时间的向量。则式（8-8）可表达成以强调时间控制点s处运行偏差的随机性。

采用γ1和γ2两个非负参数分别表征时间控制点处早到与晚到的惩罚系数，其值可根据时刻表设计人员的偏好进行取值。时间控制点s处考虑对早到和晚到惩罚的随机广义运行偏差为

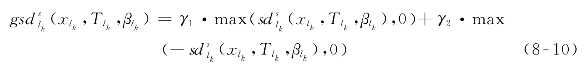
式中——公交线路l车次k在时间控制点s处实际到站时刻与计划到站时刻之间的广义偏差（min）。

显然，区段上的计划运行时间（平均运行时间加上松弛时间）应该使广义运行偏差最小。然而，由于公交运行和驾驶员行为的双重随机性，对于不同的仿真运行或者试验运行，如果仅仅要求运行偏差的均值是最优的，可能会出现运行偏差值存在很大的波动。故如式（8-11）所示，不仅计算时间控制点s处随机广义运行偏差的均值，同时还度量随机广义运行偏差与其均值的绝对差值（即为平均绝对偏差[68，212]），以反映随机广义运行偏差的波动性。在数理统计上，平均绝对偏差是所有单个观测值与算术平均值的偏差的绝对值的平均，即对同一物理量进行多次测量时，各次测量值及其绝对误差不会相同，将各次测量的绝对误差取绝对值后再求平均值。

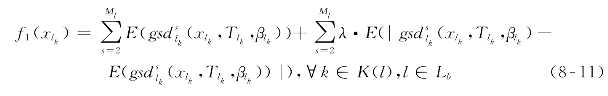
式中：f1（xlk）——公交线路l车次k实际运行与计划时刻表的偏差（min）；

λ——非负权重参数，表征减少运行偏差波动的重要性，即反映决策者对运行偏差波动性的风险规避。

2.换乘等待时间分析

若在时间控制点s处公交车辆上乘客可换乘至轨道交通线路，则由轨道交通线路上末班列车在轨道交通站点处的计划离站时刻、轨道交通线路上计划发车间隔、从时间控制点s至轨道交通站点的平均步行时间和公交线路l车次k在时间控制点s处的计划到站时刻，可知车次k上乘客在轨道交通站点处的换乘等待时间（即与时间控制点s相关的换乘等待时间），具体计算参见式（8-12）。

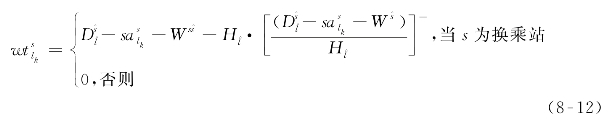
式中——公交线路l车次k在时间控制点s处的换乘等待时间（min）；

—研究时间范围内轨道交通线路上末班列车在轨道交通站点处的计划离站时刻；

——从时间控制点s至轨道交通站点的平均步行时间（min）；

——研究时间范围内轨道交通线路计划发车间隔（min）；

[]-——向下取整操作。(www.xing528.com)

相应地，公交线路l车次k在各时间控制点处的换乘等待时间总和为

式中：——公交线路l车次k上乘客的换乘等待时间（min）。

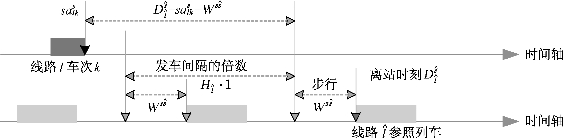
图8-4　地面公交换乘轨道交通示意图

如果轨道交通上乘客可在时间控制点s处换乘至某一公交车辆，根据轨道交通线路上末班列车在轨道交通站点处的计划到站时刻、轨道交通线路上连续两列列车之间计划发车间隔、从时间控制点s至轨道交通站点的平均步行时间、公交线路l车次k在时间控制点s处的计划到站时刻和实际停靠时间，可知轨道交通线路上乘客换乘至公交线路l车次k时在时间控制点s处的最短换乘等待时间，具体计算参见式（8-14）。

式中——轨道交通线路上乘客换乘至公交线路l车次k时在时间控制点s处的最短换乘等待时间（min）；

——研究时间范围内轨道交通线路上末班列车在轨道交通站点处的计划到站时刻；

——公交线路l车次k在时间控制点s处实际停靠时间（min），可根据历史数据估计；

[]+——向上取整操作。

通常线路多班列车上乘客均可换乘至公交线路l车次k，由于研究时间范围内线路拥有均匀发车间隔，故只要保证与公交线路l车次k换乘成功的列车车次中换乘等待时间最短的一班列车的换乘等待时间最小即可保证其他换乘成功的列车车次换乘等待时间亦是最小，如图8-5所示。故仅需以与公交线路l车次k换乘成功的列车车次中换乘等待时间最短的一班列车的到站时刻为协同对象。相应地，成功换乘至公交线路l车次k的等待时间最短的列车车次上乘客换乘等待时间总和为

式中——成功换乘至公交线路l车次k的等待时间最短的列车车次上乘客换乘等待时间总和（min）。

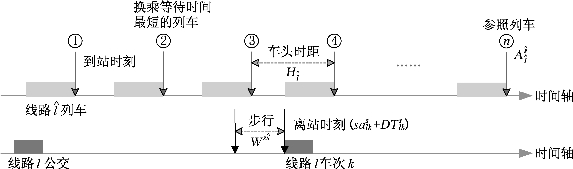
图8-5　轨道交通换乘地面公交示意图

3.优化模型构建

根据上述分析，时间控制点时刻表设计问题的目标函数可表达为

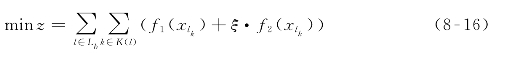
式中：z——目标函数值（min）；

ξ——时间控制点处换乘等待时间的惩罚系数。

式（8-16）中惩罚系数ξ表示减少换乘等待时间在时间控制点时刻表设计中的重要性，其值同样可根据时刻表设计人员的偏好确定。当ξ=0时，则上述优化模型未将地面公交与轨道交通的协同调度要求纳入考虑，为常规的地面公交单线路时间控制点时刻表设计模型。

时间控制点时刻表设计问题同时还需要考虑如下两个重要约束条件：

式中：Hl——研究时间范围内公交线路l计划发车间隔（min）；

Vl——公交线路l上车辆配备数量（辆）；

Cl——公交线路l的计划半循环时间（min）。

式中：υmin——松弛时间取值的下限（min）；

υmax——松弛时间取值的上限（min）。

式中：Z——整数集合。

约束条件（8-17）表明各区段上的松弛时间的总和不大于由配备的公交车辆数、计划发车间隔和计划半循环时间所决定的总松弛时间的最大值0.5·Hl·Vl-约束条件（8-18）定义了决策变量的取值范围，实践中，参数υmax与υmin可根据实际情况进行灵活调整。另外，为了使设计的时刻表在实际中易于操作执行，要求各区段上的松弛时间为以分钟为单位的整数变量，如式（8-19）所示。

同一时间控制点处往往有多条公交线路需要与同一轨道交通线路进行协同调度，然而由于公交站点处泊位数有限，实施协调优化后可能会引起公交车辆在站点附近排队，使得部分公交车辆无法及时进站，进而导致车上换乘乘客错过最近的一班轨道交通列车（即实施协调优化后等待时间最短的一列车次），甚至会发生在他们走至换乘站台的过程中眼看着列车离开的情况。增加约束条件（8-20）～（8-22），旨在消除这一不受欢迎的协调优化的潜在“副产品”。这三个约束条件可以实现以下两个要求：公交线路l上车次k在时间控制点s处的计划到站时刻必须分配给一个唯一的时间点j；连续φs个时间点上所分配的公交车辆在时间控制点s处的计划到站时刻的个数不超过Bs。时间控制点s处的公交车辆泊位数Bs的取值可通过实地调查获取。公交车辆在时间控制点s处的最长停靠时间φs（以分钟为单位）的值可根据历史数据估计而得。若由历史数据统计所得实际停靠时间最大值（以分钟为单位）并不是整数，则进一步向上取整。此时，φs为取整后的整数。集合J包含覆盖整个研究时间范围内的各个时间点，而j则代表隶属于该集合的某一具体的时间点。举例说明，若J=[08：00，08：01，08：02，…，09：29]，则到站时刻08：29会被分配到第30个时间点；若Bs=2和φs=3，则约束条件（8-20）～（8-22）意味着每连续3 min内最多只能有2辆公交车停靠在时间控制点s处。

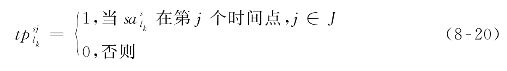
式中——二元变量：当公交线路l车次k在时间控制点s处的计划到站时刻在第j个时间点时，等于1；否则等于0。

式中：φs——时间控制点s处车辆实际停靠时间的最大值（min）；

Bs——时间控制点s处的公交车辆停靠泊位数（个）。

综上所述，基于协同调度的时间控制点时刻表可通过求解以下随机混合整数非线性规划模型获取。

目标函数：式（8-16）

约束条件：基本约束：式（8-1）～（8-13）、（8-17）、（8-18）

排队约束：式（8-20）～（8-22）

通过引入非负辅助决策变量和式（8-11）中绝对值表达式可线性化，如式（8-23）～（8-25）所示。

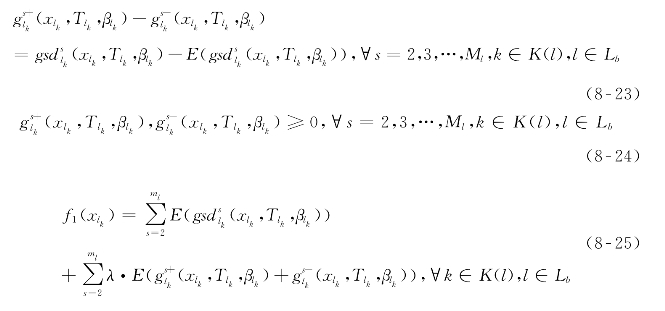
而约束条件（8-20）等价于约束条件（8-26），通过引入非负辅助决策变量和可进一步进行线性化处理，最终转化为式（8-27）～（8-30）。

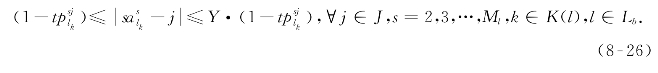
式中：Y——一个足够大的已知正数。

最终所构建的随机混合整数非线性规划模型便等价于以下随机混合整数线性规划模型：

目标函数：式（8-16）

约束条件：基本约束：式（8-1）～（8-10）、（8-25）、（8-12）、（8-13）、（8-17）、（8-18）、（8-23）、（8-24）

排队约束：式（8-27）～（8-30）、（8-21）、（8-22）