城市多模式公共交通运行协调方法的算例分析结果

以4条（仅考虑了早高峰客流集中的4个行车方向）具有换乘关系的公交线路构成的网络为例验证上述时刻表协调优化模型的有效性和求解算法的可行性。这4条公交线路（分别命名为线路1、线路2、线路3和线路4）的沿线换乘站点及其相互间换乘关系见图6-16（图中省略了非换乘站点）。实际公交网络内存在异站换乘的现象，但大部分乘客在制订出行计划时倾向于选择同站换乘的出行路径。为了简化计算，算例中仅考虑了同站换乘关系。尽管由4条线路构建的网络与实际中区域或城市公交网络规模等级上存在巨大差距，但通过研究该网络已可定量验证模型与算法的有效性。此规模也更便于读者重复整个验证过程。

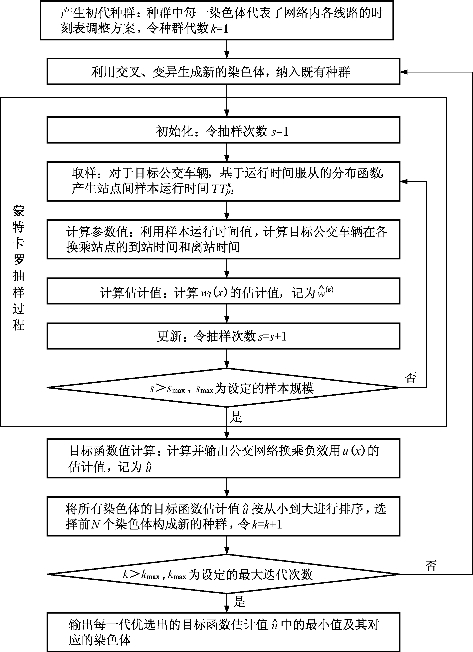
图6-15　包含蒙特卡罗仿真的遗传算法流程图

图6-16　公交线路布局图

表6-12给出了研究时间范围内（7：00 am—8：00 am）每条公交线路的现状运行参数，包括各班公交车首站计划发车时刻和各换乘站点间运行时间均值。

表6-12　研究时间范围内公交线路现状运行参数

假定任意连续两个换乘站点间的车辆实际运行时间均服从对数正态分布，即且仅在区间内取值。表6-12已给出了各运行时间分布函数对应的均值设换乘站点间运行时间变异系数为0.3，即；令换乘站点间运行时间取值范围为即且公交车辆在各换乘站点处实际停靠时间统一设为0.5 min，同一站点内换乘步行时间统一设为0.5 min，目标函数中权重值λ设为0.5。

1.算例结果分析

采用包含蒙特卡罗仿真的遗传算法进行求解，交叉率Pc和变异率Pm分别为0.65和0.20，种群规模为100，种群最大代数kmax为500。蒙特卡罗仿真方法的样本规模L为50。在MATLAB（R2013a）平台编写求解程序，所有计算过程在一台内存为8G的台式机（Intel Core i3-2100 CPU@3.10GHz）上完成。(www.xing528.com)

包含蒙特卡罗仿真的遗传算法具体迭代进化过程见图6-17。其中，换乘负效用值随着迭代次数的增加逐步下降，进化至第18代时已趋于稳定（蒙特卡罗抽样的随机性导致相同染色体对应的换乘负效用存在差异，故曲线呈现波动性稳定），表明所设计的遗传算法具有较好的收敛性。

图6-17　遗传算法迭代进化曲线

表6-13给出了目标线路的时刻表偏移方案，即研究时间范围内线路1和线路2各车次均需提前6 min从首站发车；而研究时间范围内线路3和线路4各车次均需延迟5 min从首站发车。此时刻表偏移方案下对应的换乘负效用u（x）为281.75 min。然而，当按照现状时刻表正常运行时乘客所感知的换乘负效用u（x）的计算结果为363.34 min，见表6-14。与现状时刻表相比优化后时刻表可有效降低约22%的总换乘负效用，能切实改善公交网络内换乘服务。

表6-13　时刻表偏移方案：遗传算法（单位：min）

2.算法有效性验证

为了验证包含蒙特卡罗仿真的遗传算法的有效性，采用枚举算法计算全局最优解，根据4个整数决策变量的取值范围，可知时刻表调整方案共有20 449组。对所有的方案进行枚举并采用蒙特卡罗仿真方法计算目标函数值，如表6-14所示，得到换乘负效用u（x）的最小值为294.64 min，最大值为405.44 min，均值为356.74 min。除了最小值和最大值，表6-14中亦列出了排在前5位（按换乘负效用值从小到大排序）的换乘负效用值及其对应的时刻表偏移方案。

表6-14　时刻表偏移方案：枚举算法（单位：min）

对比表6-13和表6-14可知，遗传算法得到的优化方案与枚举算法得到的第5位优化方案相同。需要注意的是尽管两者方案相同，但由于蒙特卡罗抽样的随机性使得其各自对应的换乘负效用值存在些微差异。另外，由表6-14易知前5位各自对应的换乘负效用值之间的差异基本可忽略不计，即所设计的包含蒙特卡罗仿真的遗传算法可以有效地计算得到近似最优解。对表6-14和图6-17进行综合分析后可知该遗传算法可行且高效。