公交系统中换乘时间和调度性能的算例分析和结果

共线线路1、线路2和线路3共用5个停靠站，如图6-8所示。研究时间范围设为6：30am—7：30am，也就是说仅考虑在这一小时以内分别从首站发出的公交车次。线路1、线路2和线路3目标车次的首站计划发车时刻均设定为6：30am（车次1）、6：45am（车次2）、7：00am（车次3）和7：15am（车次4），意味着这3条公交线路在研究时间范围内均以均匀的发车间隔（15 min）从首站依次发车。共线段内线路间换乘需求参见表6-8。

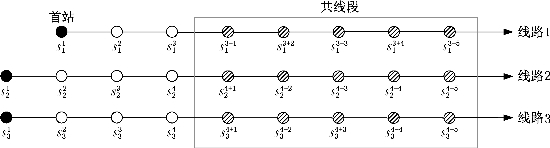
图6-8　线路1、线路2和线路3

假定任意连续两个公交站点间的车辆实际运行时间均服从对数正态分布，即且仅在区间内取值。其中和分别表示公交线路r车次j在线路段i随机运行时间的均值和标准差和分别表示公交线路r车次j在线路段i随机运行时间的下限和上限。为了简化计算，对于所有的站点间实际运行时间，参数和取值均相同。具体地，所有的站点间实际运行时间均服从对数正态分布LN（2，1），并仅在区间[1，5]内取值。另一个影响公交车辆在换乘站点处到站时刻、离站时刻的重要因素为公交车辆站点停靠时间。假定线路1和线路2在共线段内各换乘站点处的停靠时间累计差值（即线路1在到达某一换乘站点前上游各站点处停靠时间的总和减去线路2在到达同一换乘站点前上游各站点处停靠时间的总和）分别为0.5 min、0.5 min、0.3 min、1.0 min和0.5 min。类似地，线路1和线路3在共线段内各换乘站点处的停靠时间累计差值分别为-0.3 min、0.2 min、0 min、0.4 min和0 min。相应可知，线路2和线路3之间在共线段内各换乘站点处的停靠时间累计差值分别为-0.8 min、-0.3 min、-0.3 min、-0.6 min和-0.5 min。同时假定各车次在共线段内各换乘站点处的停靠时间均为0.5 min。考虑到所有的换乘均为同站换乘，令换乘步行时间WTk等于0.5 min。另外，令目标函数中权重值λ等于0.5。

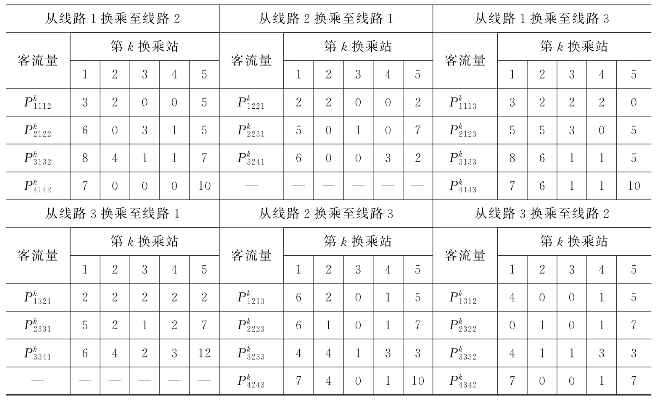
表6-8　换乘需求（单位：人）

1.样本规模分析

样本均值近似方法解的质量很大程度上取决于样本集合数和样本规模。分析不同样本规模下解的质量可为最终确定合理的样本集合数和样本规模提供指导和参考。在本算例的样本均值近似过程中，设定样本集合数M=20、样本规模

采用YALMIP语言[203]在MATLAB（R2013a）平台编写求解程序，并调用CPLEX 12.6求解样本均值近似问题。CPLEX为IBM ILOG开发的一款包含分支定界法的优化软件包，可用于求解线性规划、二次规划、二次约束规划及混合整数规划等问题。具体计算过程在一台内存为16G的台式机（Intel Core i7-2600 CPU@3.40GHz）上完成。

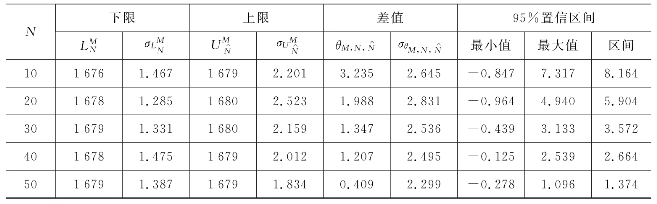
表6-9给出了当样本规模N分别为10、20、30、40和50时目标函数值的上限、下限、上限与下限之间差值以及差值的95%置信区间。根据表6-9的结果可知，随着样本规模的增加，上限与下限之间差值的95%置信区间相应变窄。考虑到样本规模为50时95%置信区间范围已能满足计算精度要求（即小于1.5，精度要求可根据实际需要灵活调整），最终确定本算例样本规模设定为50。后续所有相关计算时，样本集合数M=20、样本规模N=50。

表6-9　样本均值近似方法相关分析参数（单位：min）

(www.xing528.com)

样本规模N=50时，算例中线路时刻表经协调优化后的乘客所感知的换乘负效用为1 679 min，相应的最优时刻表调整方案参见表6-10。与现状时刻表下乘客感知的换乘负效用（2 530 min）相比，调整后时刻表可以减小约51%的换乘负效用，说明所构建的优化模型可切实有效地改善线路间换乘服务。

表6-10　时刻表调整方案（单位：min）

2.DTOM和ATOM比较 分析

6.2.2节提出的时刻表优化方法考虑了共线段内乘客对换乘站点的偏好差异，简称为非集计方法DTOM（Disaggregate Transfer Optimization Method），假定线路间换乘乘客均在同一站点换乘的时刻表优化简化方法，简称为集计方法ATOM（Aggregate Transfer Optimization Method），二者的适应性分析对换乘协调优化实践有着重要的指导意义，尽管6.1节对此已展开了较为细致的讨论，本节在评价6.2.2节所构建的优化模型效能的基础上仍将分析不同情景下DTOM和ATOM的适应性，以进一步验证6.1节的分析结论。

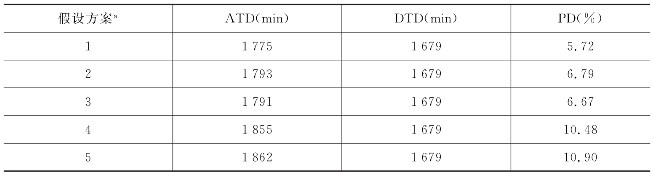
一方面，计算假定所有乘客都在同一站点进行换乘时的目标车辆首站计划发车时刻最优调整方案，并计算当时刻表按照上述方案调整后实际换乘客流分布下乘客感知的换乘负效用，定义为集计负效用ATD（Aggregate Transfer Disutility）；另一方面，考虑实际换乘客流分布利用DTOM求解其首站计划发车时刻最优调整方案及其相应的换乘负效用，定义为非集计负效用DTD（Disaggregate Transfer Disutility）；两者之差（ATD减去DTD之后的差值）即为未考虑乘客偏好差异所引起的额外负效用。由表6-11可知，五种假设方案下ATD减去DTD之后的差值均为正数，即假定所有乘客都在同一站点进行换乘时得到的目标车辆首站计划发车时刻最优调整方案（ATOM的最优解）会引起额外的换乘负效用。然而各假设方案下ATD值均小于现状时刻表下乘客感知的换乘负效用值（2 530 min），表明即便是简化方法ATOM亦可有效减少线路间换乘等待时间。

表6-11　不同假设方案下PD值

注：a.数字1表示假定所有换乘乘客均选择在进入共线段后第1个换乘站点处进行换乘；数字2表示假定所有换乘乘客均选择在进入共线段后第2个换乘站点处进行换乘；依次类推。

定义用ATOM引起的额外负效用与DTD的比值来衡量ATOM引起的偏差程度，简称PD（Percent of Deviation）指标，即

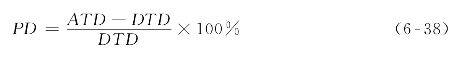
在表6-11内，五种假设方案下指标PD的值分别为5.72%、6.79%、6.67%、10.48%和10.90%，进一步说明当实际换乘客流分布获取难度或代价过高时，所有乘客均在同一站点完成换乘的假设是可以被接受的，而且此时若假定所有乘客都在进入共线段后第一处站点进行换乘则可最大限度地减小忽略换乘偏好差异引起的额外负效用，该结论与6.1节分析结论相一致。