Kleywegt等[199]提出的样本均值近似方法(Sample Average Approximation,SAA)是基于蒙特卡罗仿真方法的随机问题求解方法。其中,样本均值近似方法的关键步骤如下:生成随机运行时间向量TT在N个情景下的独立同分布的随机样本向量TT1,…,TTN,则期望值![]() 可由样本均值
可由样本均值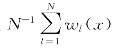 近似。
近似。
样本均值近似方法及相关统计参数估计的具体步骤如下:
Step 1:产生M组随机样本集合,其中每组样本集合内包含N个随机样本,即![]()
Step 2:利用分支定界法求解每组样本集合对应的样本均值近似问题。令![]() 和
和![]() 分别表示样本均值近似问题的最优解和相应的目标函数值。
分别表示样本均值近似问题的最优解和相应的目标函数值。
Step 3:利用公式(6-31)计算上述随机优化模型目标函数值下限的点估计,相应的点估计的方差可按式(6-32)进行计算。
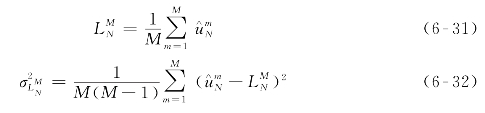
Step 4:对应于Step2中计算所得每一个最优解![]() ,独立地产生另一组随机样本集合
,独立地产生另一组随机样本集合![]() 该集合内将包含
该集合内将包含![]() 个样本
个样本![]() 远大于N),然后计算以下表达式
远大于N),然后计算以下表达式
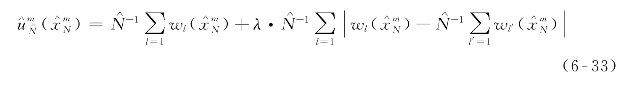
已知![]() 是随机优化模型的可行解,则
是随机优化模型的可行解,则![]() 为该随机优化模型目标函数值上限的无偏估计,进而可知最佳上限为
为该随机优化模型目标函数值上限的无偏估计,进而可知最佳上限为
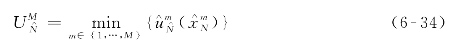
令![]() 则
则![]() 的方差可按下式估计
的方差可按下式估计
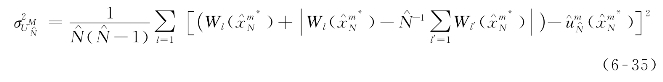 (https://www.xing528.com)
(https://www.xing528.com)
Step 5:计算目标函数值上限![]() 与下限
与下限![]() 之间的差值
之间的差值
![]()
相应地,差值![]() 的方差为
的方差为
![]()
Norkin等(1998)[200]和Mak等(1999)[201]已经证明![]() 的期望值小于等于最优解u*,即
的期望值小于等于最优解u*,即![]() 然而由于无法获取
然而由于无法获取![]() 的精确值
的精确值![]() 的期望值只能近似由均值(即期望值的无偏估计)替代。为了计算均值,首先需要产生M组随机样本集合(Step 1),然后利用公式(6-31)计算平均值
的期望值只能近似由均值(即期望值的无偏估计)替代。为了计算均值,首先需要产生M组随机样本集合(Step 1),然后利用公式(6-31)计算平均值![]() 。由于计算所得的均值
。由于计算所得的均值![]() 是期望值
是期望值![]() 的无偏估计,所以
的无偏估计,所以![]() 小于等于最优解u*,即
小于等于最优解u*,即![]() 是最优解u*的下限。
是最优解u*的下限。
在利用样本均值近似方法将随机混合整数线性规划模型转化为确定的混合整数线性规划模型后,即可利用分支定界法(branch and bound)获取模型最优解。分支定界法是一种求解整数规划问题的常用策略[202]。该方法不但可以求解纯整数规划,还可以求解混合整数规划问题。混合整数线性规划问题(同时为最小化问题)的分支定界过程包括以下步骤:
Step 1:利用单纯形法求混合整数规划松弛问题(线性规划问题)的最优解。若松弛问题的最优解满足整数要求,得到整数规划的最优解,否则转至Step2。
Step 2:任意选一个非整数解为实数Bi的变量xi,令[Bi]为Bi的整数部分,在原松弛问题中分别加上约束xi≤[Bi]及xi≥[Bi]+1组成两个新的松弛问题,称为分支。
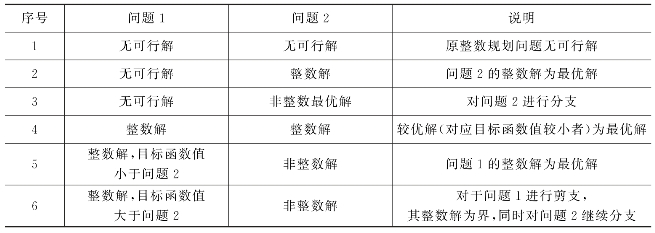
Step 3:利用单纯形法求解新的松弛问题,即定界过程。设两个分支的松弛问题分别为问题1和问题2,它们的最优解情况如表6-7所示。其中,情况2、4、5即为第一轮分支后即找到最优解;情况3则需要在相应缩减的可行域上继续下一轮的分支定界过程;情况6中问题1的整数解作为界被保留,用于以后与问题2的后续分支所得的解进行比较,结论为情况4或情况5。
表6-7 松弛问题可行解情况
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




