城市公交运行协调方法

地面公交系统可以满足大部分居民的公共交通出行需求。乘客可利用地面公交从市郊居住区抵达城市中心区，也可穿过中心区到达位于城市另一端的市郊工业园区。对于长距离出行的乘客，往往需要经历不同线路间的换乘。然而，公交线路在途经城市主要干道时往往与多条线路存在共线段，此时不同线路间存在多个可选的换乘站点，如图6-3所示。

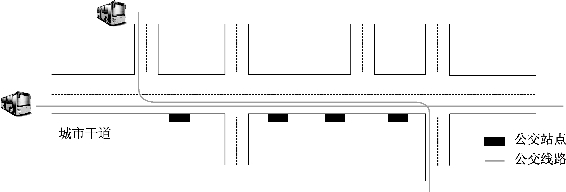
图6-3　公交共线段示意图

对于需要在共线段内换乘的乘客而言，与其他乘客在同一站点完成换乘不再是其唯一的选择。即当两条公交线路间存在多个连续可选的换乘站点时，每一位需要在这两条线路间换乘的乘客都会根据自己的偏好选择站点完成换乘。尽管不同的乘客由于偏好差异将选择不同的站点进行换乘，但对于同一位乘客，出于惯性，其每日换乘站点的选择方案往往是固定的。即乘客对换乘站点的偏好可根据历史数据估计。

由6.1.1节分析可知当两条公交线路间存在多个连续可选的换乘站点时，乘客更偏好在靠近出发地、目的地或交通便利的站点进行换乘。尽管上述偏好特征的普适性仍有待论证，但至少可以说明，乘客由于无法精确了解各个可选换乘站点处所需等待时长，在选择站点时多出于感性判断，如部分乘客倾向于在第一个可选站点处下车换乘而另一部分乘客选择在最后一个可选站点处换乘。

建模优化时刻表以改善换乘服务时为获取每一换乘站点处换乘乘客需求，公交运营企业需要耗费大量时间与资源。为了降低建模成本，是否可以按照线路间换乘乘客均在同一站点换乘的假设进行时刻表优化以达到预期目标（如减少换乘等待时间）？简化后协同调度效果是否会“大打折扣”？故本节重点探讨是否可以将公交线路共线段内多点换乘简化为单点换乘这一现实问题，以期提出科学合理且切合实际的共线线路间协同调度方法。

拟构建考虑公交线路共线段内换乘乘客实际选择偏好的时刻表优化方法（后文简称为“非集计方法”），并通过与简化方法即假定所有乘客在同一站点换乘的时刻表优化方法（后文简称“集计方法”）的对比分析研究忽略乘客对换乘站点偏好的异质性对协调优化效果的影响。

1.问题描述与假设条件

设编号依次为1，2，…，r，…，R的R（R≥2）条共线公交线路间存在K（K≥2）个编号依次为1，2，…，k，…，K的连续可选换乘站点。每一条线路的上下行被分别视作独立的研究对象。由于每条线路上下行的客流高峰期往往属于两个不同的时段（如分别位于早高峰和晚高峰），故在特定的研究时间范围内（如早高峰）仅需考虑每一条线路客流集中的行车方向（即某一特定的行车方向）。每条公交线路以均匀的发车间隔从首站发车。以线路r为例，以发车间隔Hr从首站发车，每辆公交车在抵达共线段内第一个换乘站点前已途经包括首站在内的Mr个公交站点，如图6-4所示。

图6-4　共线公交线路

研究将建立在以下假设基础上：（1）现状公交线路各自按照未经协调的时刻表运行；（2）每一换乘站点处换乘乘客数量固定且已知；（3）调度员仅能保证公交车辆从首站准点发车，途中并未采取任何控制策略以保证车辆运行可靠性；（4）所有公交车辆性能相同且每辆公交车的载客能力都能满足换乘需求。

共线公交线路间换乘问题的优化目标为，通过修正公交车辆首站计划发车时刻协调关联车辆在换乘站点处的离站、到站时刻，以获取使换乘过程中乘客所感知的换乘等待时间最短的首站计划发车时刻最优调整方案。

2.换乘等待时间

由于公交车辆运行的随机性，在每个换乘站点处的乘客换乘等待时间与公交车辆实际运行时间分布息息相关，而实际运行时间分布特征可根据公交运行历史数据（如AVL系统历史数据）估计。既有研究对站点间运行时间或站点处到站时刻的分布已展开了深入讨论并推荐了相应的概率密度函数，如对数正态分布[70，105，194]、伽玛分布[195-196]、正态分布[197-198]、截尾指数分布[103]等。尽管对于上述分布的适应性尚未形成统一认识，偏态分布（如对数正态分布和伽玛分布）在既有研究中得到了广泛应用。另研究发现当公交车辆运行随机性过于显著时，时刻表协调优化的效果不甚显著[144]，应该先提高单线路运行可靠性再考虑协调不同线路间时刻表以改善换乘服务。因此，假定连续两个站点间的公交车辆随机运行时间均服从于某一特定截尾对数正态分布。令表示公交线路r车次j在站点i和站点i+1间实际运行时间，其分布的概率密度函数如式（6-1）所示：

式中——随机运行时间分布的概率密度函数；

——随机运行时间分布的累积密度函数；

——随机运行时间的均值（min）；

——随机运行时间的标准差（min）；

——随机运行时间可能的最小值（min）；

——随机运行时间可能的最大值（min）；

——研究时间范围内公交线路r待协调优化车次数（班）。

令表示公交线路r车次j的现状首站计划发车时刻偏移后其在换乘站点k处的实际到站时刻，可按式（6-2）计算：(www.xing528.com)

式中——公交线路r车次j现状首站计划发车时刻；

——公交线路r车次j现状首站计划发车时刻偏移量（min）；

Mr——服务于公交线路r的车辆在抵达共线段内第一个换乘站点前已途经的站点数（个），包括首站；

K——共线段内换乘站点数（个）。

令为公交线路r车次j的现状首站计划发车时刻偏移后其在换乘站点k处的实际离站时刻，可按式（6-3）计算：

式中：——公交线路r车次j在换乘站点k处的实际停靠时间（min）。

根据关联车辆的到站时刻、离站时刻，即可按式（6-4）计算乘客在换乘站点处的等待时间。

式中——在换乘站点k处从公交线路r车次j换乘至公交线路r'车次j'的等待时间（min）；

WTk——在换乘站点k处不同车辆间换乘步行所需时间（min）；

Hr'——研究时间范围内公交线路r'计划发车间隔（min）。

3.换乘负效用

换乘负效用函数u（x）可用来表达在换乘过程中乘客所感知的换乘等待时间。既有文献中多选择用平均换乘等待时间度量换乘负效用，即令u（x）=E（x）。尽管此做法由于计算相对简单得到了广泛应用，然而由于公交运行的随机性，对于不同的仿真运行或者试验运行，如果仅仅要求换乘等待时间的均值是最优的，可能会使得换乘等待时间存在很大波动。采用换乘等待时间的均值衡量换乘负效用时默认对于长时间等待情况和短时间等待情况赋予同样的权重，未考虑乘客对于换乘等待时间稳定性和可靠性的需求。具体举例说明如下：假定情景一中换乘等待时间为5 min和25 min的概率相同，而情景二中换乘等待时间恒定为15 min，则此时乘客往往更愿意接受情景二以保证在换乘过程中不会出现等待时间极值而打乱整个出行计划。故定义换乘负效用函数u（x）=E（x2）。根据方差表达式E（x2）=[E　（x）]2+Var（x）可知所定义的换乘负效用函数可以充分反映换乘等待时间分布的波动特征，使得优化方案更加合理。

换乘问题的优化目标是使共线段内所有换乘站点处的负效用总和最小，故目标函数表达为

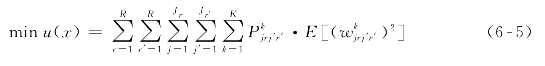
式中：u（x）——线路间总换乘负效用（min2）；

——在换乘站点k处从公交线路r车次j换乘至公交线路r'车次j'的乘客数（人）。

需要注意的是，非集计方法中，为换乘站点k处实际换乘乘客数；而集计方法中，若换乘站点k为简化站点（即假定线路间所有换乘乘客都在换乘站点k处进行换乘），则为共线段内K个换乘站点处换乘乘客数总和；否则令

目标函数（6-5）中决策变量为各车次首站计划发车时刻的调整幅度约束条件（6-6）表明了决策变量可能的取值范围，保证首站发车时刻的调整幅度不会严重影响车辆发车频率，即无需调整车辆调度计划和司乘调度安排。因此，在进行时刻表优化时未考虑由车辆运行计划调整引起的企业运营成本变化。另外，为了保证设计的时刻表在实际中易于操作执行，将首站计划发车时刻偏移量设置为以分钟为单位的整数变量。由此可知，所提出的协调优化方法可作为一个有用且符合实际的定量分析工具协助公交企业的日常调度管理。

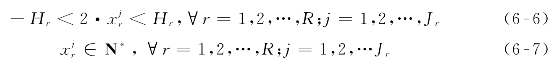
式中：N*——正整数集合。

仅要求一部分决策变量必须取整数值的规划问题称为混合整数规划问题。不考虑整数条件，由余下的目标函数和约束条件构成的规划问题称之为该混合整数规划问题的松弛问题。若松弛问题是一个（非）线性规划问题，则称该规划问题为混合整数（非）线性规划问题。可见上述所构建的优化模型为混合整数非线性规划模型，作为NP难问题很难通过精确搜索算法获取其全局最优解。另一方面，当共线的公交线路数超过两条时，利用枚举方法求解时将耗费大量时间。例如当R=4且H1=H2=H3=H4=15时，决策变量取值范围内最多可包含154=50 625个可行解，显然此时枚举方法的适应性有待商榷。故推荐采用启发式算法如遗传算法以保证在可接受的计算费用/时间内获取近似最优解。由于本节研究的重点为通过对比非集计方法和集计方法协调优化效果分析忽略乘客对换乘站点偏好的异质性对换乘协调优化效果的影响，因此关于启发式算法的适应性及其计算效率分析将暂不考虑。事实上，6.2节将通过修正上述混合整数非线性规划模型以获取模型的精确解（全局最优解）。6.1.3节基于仿真的小规模算例分析中，采用枚举算法求取最优解。