1.模型构建
如何以合理的运营成本为乘客提供满意的服务，是编制行车时刻表的核心问题。乘客总是期望企业能够提供高频的公共交通服务，而企业出于成本考虑则期望尽可能降低发车频率。乘客对服务品质的需求与企业对经济利益的诉求间的矛盾客观存在，但并非不可调和。公共交通服务水平提高则可以吸引更多的居民选择乘坐公共交通，企业运营效益随之增长，相应地可增加投入进一步提升改善公共交通服务质量，乘客需求被更好地满足。因此，从乘客和企业双方利益最大化出发，根据客流量实际分布情况，以乘客车外等待时间、乘客车内舒适度、企业效益成本比率的加权和最小为目标，建立发车间隔分时段多目标组合优化模型。
由于公共交通运营调度具有影响因素众多、外部环境复杂、客流波动显著等特点，在建立优化模型前需对实际情况进行适当简化。主要假设条件如下：
①乘客到达规律符合均分分布，任何时段内各站点上下车客流情况与断面客流情况已知；
②同一时段内采用相同的发车间隔；
③所有车辆车型、性能完全相同，且总可以按照计划准时进/出站；
④采用一票制收费方法，即票价与乘坐距离无关；
⑤车辆容量总是可以满足需求，即所有候车乘客均可顺利乘坐其到站后首班到站的目标车辆离开。
为了表达清晰，下文中用希腊字母和大写字母表示已知参数而用小写字母表示未知的决策变量。
当车外等待时间超出乘客所能容忍的极值时，乘客会产生不满、抱怨的情绪，甚至不再选择公共交通服务出行。调度人员在编制行车时刻表、确定发车间隔时应尽可能减少等待时间超出乘客容忍极限的情况，即模型的优化目标之一是极小化抱怨等待时间过长的乘客所占比例。
由于假设所有候车乘客均可顺利乘坐其到站后首班到站的目标车辆离开（即不考虑车辆载客能力的限制），故乘客车外等待时间最大值等于一个发车间隔hj，因此，当hj＞Wj时，第j个时段内才有可能存在抱怨候车时间过长的乘客。又由于假设站点处乘客到达规律符合均匀分布，故第j个时段内抱怨车外等待时间过长的乘客数
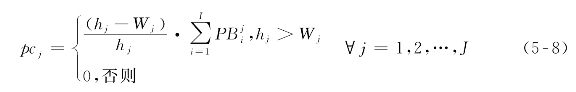
式中：J——整个研究时段内所划分的客流时段数（个）；
I——线路某一方向（上行/下行）所途经的站点数（个）；
pcj——第j个时段内抱怨等待时间过长的乘客数（人）；
hj——第j个时段内的线路发车间隔（min）；
Wj——第j个时段内乘客所能接受的最长等待时间（min）；
——第j个时段内在站点i处上车的乘客数（人）。
则整个研究时段内抱怨车外等待时间过长的乘客所占比例
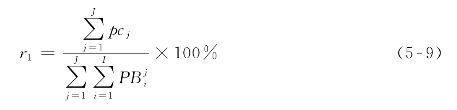
式中：r1——抱怨等待时间过长的乘客所占比例。
当车内过度拥挤时，乘客乘车体验较差，尤其是当拥挤状态持续时间较长时，同样会引起乘客的严重不满。因此，在保证乘客有车可乘的同时应尽可能为乘客提供舒适愉快的乘车体验。换言之，调度人员确定/优化发车间隔时不仅需要关注乘客候车时间，也需要关注运力与需求的匹配情况，即模型的另一个优化目标是极小化拥挤状态下车辆运行里程所占比例。第j个时段内拥挤状态下车辆运行里程
式中：lcj——第j个时段内拥挤状态下车辆运行里程（km）；
——第j个时段内在站点i处的断面客流量（人）；
Li——站点i与站点i+1间的间距（km）；
Tj——第j个时段的时间间隔（min）；
C——车辆的额定载客能力（人/辆）；
——乘客所能接受的最高满载率。
则整个研究时段内拥挤状态下车辆运行里程所占比例
式中：r2——车内拥挤状态下车辆运行里程所占比例。
公共交通是社会公益性事业，相较于高昂的运营成本（车辆购置、维修、保养费用、司乘人员劳动报酬、企业日常管理支出等）票款收入较为有限，尽管政府会给予必要的财政补贴和扶持，企业仍然期望能够在制订运营调度计划时，保证服务质量的同时尽可能降低运营成本，即发车间隔优化时还需考虑提高企业的效益成本比率。
企业运营效益成本比率等于运营盈利与运营成本的百分比，即
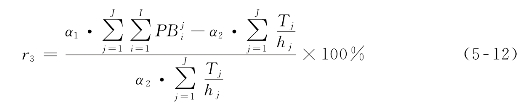
式中：r3——企业运营效益成本比率；
α1——票价（元/人）；
α2——线路单程运营成本（元）。
发车间隔优化模型需要同时考虑上述三项优化目标，最终构建目标函数
式中：z——目标函数值；
λ1——非负权重系数，表征减少乘客车外等待时间的重要性；
λ2——非负权重系数，表征提高乘客车内舒适度的重要性；
λ3——非负权重系数，表征提高企业运营效益成本比率的重要性。
调度人员可根据设计偏好和实际诉求灵活调整目标函数中非负权重系数的取值，最终编制出合理且适用的行车时刻表。
发车间隔的确定并非无约束优化问题，实际编制行车时刻表时需要考虑若干约束条件。首先需要保证车辆的平均满载率不低于企业所能接受的最低满载率标准，以保证线路运营收入能维持线路日常运营。
式中：Smin——所允许的最低满载率。(www.xing528.com)
其次，需要保证发车间隔不高于所允许的最大发车间隔Hj，即
式中：
——第j个时段内所允许的最小发车间隔（min）；
——第j个时段内所允许的最大发车间隔（min）。
参数
和
的取值通常由企业与政府协商确定。公共交通的公益性决定了企业在规定服务时间必须严格按照行业规定提供服务，即便在客流分布的平峰甚至低谷，仍要提供一定标准的服务。
另外，为避免出现乘客滞留现象，还可增加约束条件
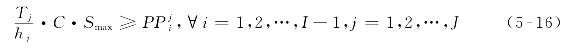
式中：Smax——所允许的最高满载率。
综上可知，通过求解以下非线性规划模型即可获取目标线路各时段合理的发车间隔方案。
目标函数：式（5-13）
约束条件：式（5-8）～（5-12）、（5-14）～（5-16）
为了降低模型求解难度，增强模型的实用价值，考虑对上述非线性规划模型进行适当的转化降低模型维度。
可通过增加辅助二元变量ypc将约束条件（5-8）转化为
式中：ypc——辅助二元变量，用于实现约束条件的线性化；
M——一个足够大的已知正数。
约束条件（5-17）和（5-18）表明，当且仅当hj＞Wj时，ypc等于1，即
其他情况下，ypc等于0，即pcj=0。
类似地，通过增加辅助变量ylc，可将约束条件（5-10）转化为
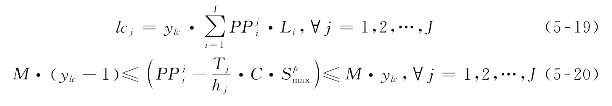
式中：ylc——辅助二元变量，用于实现约束条件的线性化。
考虑到发车间隔与发车次数的关联系
式中：nj——第j个时段内发车次数（班）。
将模型中所有的发车间隔hj变量均替换为发车次数nj变量，则约束条件（5-17）和（5-18）分别更新为约束条件（5-20）相应更新为
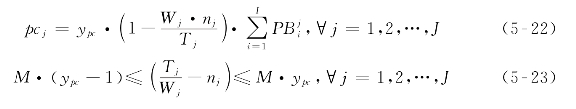
约束条件（5-12）相应更新为
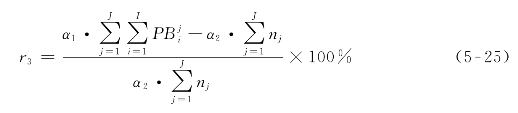
为了进一步降低模型维度，约束条件（5-25）可调整为约束条件（5-26），同样可用于表征企业运营经济性。
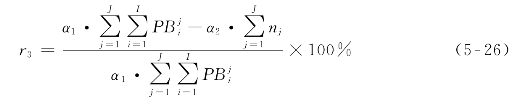
约束条件（5-14）、（5-15）和（5-16）则分别更新为
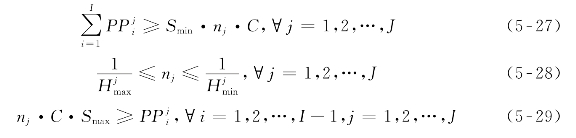
考虑到调度计划的实际应用，增加约束条件（5-30）保证发车次数nj取值的合理性，即必须为正整数。
式中：N*——正整数集合。
至此上述以发车间隔hj为决策变量的非线性优化模型可转化为以下以发车次数nj为决策变量的混合整数二次规划模型。
目标函数：式（5-13）
约束条件：式（5-9）、（5-11）、（5-19）、（5-22）～（5-24）、（5-26）～（5-30）
可利用包含分支定界法进行模型求解，获取各时段发车次数的精确解，继而根据发车间隔与发车次数的关联性，即约束条件（5-21），可推导出各时段平均发车间隔方案，继而编制出完整的行车时刻表。
2.演示算例
某一线路根据客流分布情况可将整个服务时长5：00～23：00划分为5个连续时段，分别为5：00～6：00、6：00～9：00、9：00～16：00、16：00～18：00和18：00～23：00。各时段内线路在沿线14处站点（包含首末站点）上车乘客数和断面通过量已列于表5-2。现需要确定服务时长内各时段发车间隔方案。
各时段内所允许的最大发车间隔
分别为15 min、5 min、10 min、5 min和15 min。各时段内所允许的最小发车间隔
统一设为1 min。同时，假设各时段内乘客所能接受的最长候车时间Wj分别为10 min、4 min、8 min、4 min和10 min。《城市公共交通分类标准》（CJJ/T 114—2007）中将定员数量小于等于80人的公共汽车定义为适用于支路以上等级道路的中型公共汽车，故本算例中假设企业统一采用额定载客能力C为80人/车的车辆运送乘客。所规定的线路最低满载率Smin和最高满载率Smax分别为0.5和1.2。乘客所能接受的最高满载率
假设等于0.9。线路票价α1统一设为2元。线路单程运营成本α2包括人员报酬、油费支出和其他费用等，其值可根据企业财政分析报告估算，此算例中设为70元。目标函数中的非负权重系数α1、α2和α3分别设置为0.5、0.4和0.1。
表5-2 各站点处上车乘客数与断面通过量
采用YALMIP语言在MATLAB（R2013a）平台编写求解程序，并调用包含分支定界法的整数规划求解器CPLEX 12.6获取模型最优解。所有计算过程在一台内存为8G的台式机（Intel Core i3-2100 CPU@3.10GHz）上完成。模型求解后获得的各时段发车次数与平均发车间隔方案列于表5-3。
表5-3 各时段发车次数与平均发车间隔方案
构建发车间隔优化模型时可以选择不同的指标衡量乘客与企业各自的利益，上述将乘客候车时间、车内拥挤状态、企业盈利情况作为优化项的模型，只是其中一种可能的建模方案，并非完全适用于所有情况。实际应用时可结合线路特征、时段特点等灵活选取衡量指标进行优化，建模方法也不一定局限于所介绍的单层多目标组合优化方法。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
