空时与引力统一理论的体制-量子动态宇宙探讨基本问题

1）空时的度量特征与引力重整化

双变量理论是关于空时与引力二者的统一理论，该理论认为，狭义与广义相对论分别是关于空时与引力各自的经典理论。在双变量度量理论的构建上，我们已指出，空时（含平坦空时M'与弯曲空时M）的完整获得机制与引力的重整化有关，而且空时对这一理论在体制上的发展将起着决定作用。据此，双变量理论在体制上，将有不同的特殊形式存在。这里，我们将对这一问题，利用空时与引力二者间的关系，展开进一步的讨论。

回顾我们建立的双变量度量理论，对于基本变量（5.35）而言，若在空时方程（5.29）和引力方程（5.21）中，分别输入

将分别得到狭义相对论或广义相对论（可参见图5.2）。在双变量度量理论看来，由于密码功能的遗失，这两种理论均通向不涉及引力重整化问题的理论发展的起始支脉。对于双变量统一理论而言，这两个支脉都将走向它理论发展的（唯象）终端。从而，在双变量理论中考虑引力的重整化时，理论结构需要暂时绕开狭义与广度相对论，向前进一步发展（尽管人们最先发现的是这两种理论）；否则，理论将无继续深入发展的出路。

发展过程中，若认为

则由（5.35）式可知，将得到一种空时度量与引力扰动相互协调变动的空时与引力统一理论。这里称这种理论为空时与引力协动改变的双变量统一理论，或简称空时与引力协动理论。这一理论中引入了引力重整化机制，但由于（5.36）式的存在，其中空时度量的内在改变，仍可视为是处在一种与引力扰动的联动状态（空时度量实际上并不独立），这种空时与引力协动理论是双变量度量统一理论发展过程中出现的一种特殊形态。这一理论重整化过程中发散的消除，从规范场的角度，可认为是引力扰动作为规范场在空时中一经出现，便同时利用与之相伴的空时度量扰动，抵销了它的发散。由于空时与引力将经受相同的微分同胚变换（即可用同一坐标系描述），如上状态下产生的引力扰动与空时度量扰动之间，将可能具有相当性（即（5.36）式）。这种相当性，可视为是产生二者的引力物质源与空间时间张量功能上处于“相当状态”的结果。这将刚好导致引力发散的抵销。

当统一理论的发展不受（5.38）的限制时，即空时M的度量

中的重整化空时度量可以离开平坦度规ημν而独立改变时，这种理论即为我们通常所称谓的双变量度量空时与引力统一理论。这一理论中空时度量与引力扰动之间不存在整体联动关系，二者是各自独立的变量。

不过在这一体制下，当把重整化空时度量写成

时，重整化空时度量扰动δημν（x）与重整化空时折合度量二者间存在功能相互“抵消”而总和为零的可能，这种特定条件下，将可能存在另一种空时与引力协动理论。

由上述论证可知，如上两种空时与引力协动理论中的空时与引力的合成度量，都将最终导致广义相对论的度规表式（如得到（5.7）式）。从而，都可以对广义相对论展开更深入的解析研究，如为相对论提供具有微观生成来源、且各自满足重整化空时度量方程的空时解，这种解在空时的动态演化过程中，均可呈现Minkowski空间表观状态等。

双变量度量统一理论认为，不排除宇宙可处在它的一般理论描述之下，不过也不能排除宇宙的某个空时区域处在空时与引力协动理论描述的状态。这种区域的空时，表观上可呈现Minkowski空时状态。这种协动理论，宏观上与广义相对论具有相同性质；不过，与广义相对论对它的描述不同，它的空时与引力都是量子化的。研究表明，广义相对论是处在这种空时与引力协动理论的经典表现理论的地位。狭义相对论则是这种理论为世界界定的一种空时临界状态。

这里把狭义相对论、广义相对论、空时与引力协动理论以及完整的双变量度量空时与引力统一理论的发展概貌，及相互关系用图解的方法加以表达，见绘出的双变量理论发展脉络图，即图5.2。(www.xing528.com)

2）双变量度量空时与引力统一理论在宇宙中的体制

我们将双变量空时与引力统一理论，按由上到下的顺序，绘成图5.2。支配这一演化的密码，是空时度量与引图扰动。它们的演化，决定了理论的发展；它们的确定（或选择），决定了统一理论的具体形式与体制。图中，被阴影覆盖的，为其效应可接受直接检验的量；对于宇宙膨胀，重整化空时折合度量可参予对空时膨胀的支配。终端表式中，黑体字母为独立变量。

图5.2　双变量度量理论体制概略图

图中的Ⅰ、Ⅱ、Ⅲ代表双变量度量理论发展的三个阶段。图中两侧指向斜下方的箭头，表示生出的理论分支。箭头上方所示为产生这一分支的条件；下方为将条件输入的方程；箭头所指为产生的理论。中部的两个大箭头，代表理论主体发展路线。阶段Ⅰ为自由引力扰动未进行相互作用量子化阶段；阶段Ⅱ为引力完成了相互作用量子化的阶段，但对于空时而言，它的度量改变有可能处在协动受控状态（产生协动理论A）；阶段Ⅲ为形成完整双变量度量空时与引力统一理论阶段。这一阶段中，出现的重整化空时度量扰动δημν（x）的改变是可以独立的。这一阶段的组合度量可写成

式中，空时度量跃迁演变参量εμν（x）的独立改变，在引力重整化之后，将由重整化空时度量扰动δημν（x）执行。不过作为特殊状态，这一阶段也不排除δημν（x）与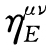（x）处在功能相互抵消，而使呈现出的空时度量为ημν的可能（产生协动理论B）。

由图5.2，并回顾空时与引力理论的发展史可知，爱因斯坦利用当时的物理学捕捉到的是关于空时与引力的最为基本的信息，分别建立的是狭义与广义相对论。这两种理论在经典水平上，至今是物理学的两种基石。对于双变量度量统一理论而言，它们也正是它关于空时与引力两个方面的基本根据。可以毫不夸张地说，这两种理论分别是双变量理论的某种特定状态，同时也是展示它全部理论的生命线与航标。然而，不能不指出，由于这两种理论只是从宏观角度来揭示空时与引力，理论体制自身无法获得更深入的微观信息，它们除了获得大量成功之外，留下的都是自身不能量子化的经典余程。也就是说，支配空时与引力量子化的信息，必须从微观另行开拓与挖掘。

空时与引力协动理论A与B，是在量子化水平上，为狭义与广义相对论提供了作为临界理论的“平台”。也就是说，狭义与广义相对论可以为这两种协动理论中的任一一种的空时与引力，提供经典唯象水平上的表述。尽管这两种协动理论中的空时与引力都已经是在深层量子化了的，但在表层外观上对行为的这种描述，也是理论所必须的。双变量度量理论也无法排除，宇宙中存在着巨大的空时区域，它的空时与引力是利用协动理论表述的（或在一定的时期是可以如此描述的）。

而双变量度量理论的最后功能是，表述空时与引力各自的独立变化以及各自的量子化，并认为宇宙空时存在的一般状态，将是处在这种完整、受控但无人为约束的自然状态。我们发现了的相对论，只是它的一种表观状态。

3）经典双变量度量理论

按双变量度量理论，引力的量子化是分为两个阶段完成的。第Ⅰ阶段为，引力扰动的激发与跃迁量子化描述阶段；第Ⅱ阶段为，引力扰动相互作用量子化的实现。这里把完成了引力量子化阶段Ⅰ、而未完成Ⅱ的引力扰动（或引力场）称为经典引力。这里讨论的双变量度量理论中的引力，将是这种经典引力。包含这种引力的双变量度量理论，也称经典双变量度量理论，它的发展略图，见图5.3。这一理论中的空时M，在图中左、右侧箭头示意下，经演绎将分别成为广义相对论中的空时M'和狭义相对论揭示的空时M'；二者都是标准的Minkowski空时。中间箭头表明，该理论的进一步发展为，利用空时方程（5.29）和引力方程（5.21）分别求出独立变量ημν（x）和hμν（x），然后得到组合度量gμν（x），进而进入验证程序。该理论在宏观把广义相对论看成是εμν≡1条件下的直接结果。这一理论中，由于未引入引力重整化机制，空时（即变量ημν（x））与引力（即变量hμν（x））始终是各自独立的，宏观物理实验对广义相对论的支持，可视为是对该理论在εμν≈1条件下的支持。

图5.3　经典双变量度量空时与引力统一理论略图

图中被覆盖的为经受检验的变量，黑体字母表示独立变量。