空时与引力统一理论的场方程及基本问题

该理论中，存在有两种动力学变量，故将有两组经典场方程存在。一组是关于引力扰动hμν的场方程；另一组则是关于变量Tμν的空时度量演化遵循的方程。

1）统一理论的引力场方程

该方程的求得，与广义相对论中利用变分原理得到爱因斯坦方程的方法类似。不过该统一理论的作用量S，应取为（5.19）式，变分变量为（5.8）式中的引力扰动hμν。这样，变分原理可写成如下形式：

式中，Tμν为质量张量。通过（5.9）式，利用（5.8）式并把（5.17）式代入上式，经过计算，将得到该统一理论的引力场方程

式中，Gμν（hλσ）为统一理论的引力爱因斯坦张量。这里把这一双变量统一理论的引力爱因斯坦张量用加黑字体Gμν（hλσ）表记，其定义为

式中，gμν≡gμν（x）为协变组合度量张量。当gμν（x）退化为gμν（x）时，即

时，有关系式成立

同时，该统一理论的引力场方程（5.20），将退化为广义相对论中的爱因斯坦方程：

若

非退化，并且进行二元世界M的相关计算时，ημν（x）和hμν（x）分别由互逆关系和（5.24）式定义。当把空时和引力分别考虑时，由度规ημν（x）和gμν（x）规定的Riemann几何，将分别适于对它们描述的空时与引力进行表述。而对于宇宙大范围而言，双变量理论认为，绝对度量gμν（x）及其建立的相关Riemann几何的分离描述图景，将被用来代替广义相对论对宇宙的宏观描述。(www.xing528.com)

2）统一理论的空时度量方程

基本变量εμν（x）的演化所遵循的方程，亦可由变分原理得到。被变分的作用量仍为（5.19）式给出的S，不过，这里的变分变量我们将取为流行M上标架场的逆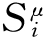（x）。从而，变分原理可写成

式中，Θμν为双变量统一理论引入的代表决定空时度量的一个量，这里称为空间时间张量[3]。把（5.16）式定义的描述空时演化的作用量Lst代入（5.28）式，可求得该空时与引力统一理论的空时度量方程，现将求得的一结果给出如下：

式中，不同形式的曲率以及统一理论的空时爱因斯坦张量Gμν（ελσ），皆由组合度量（5.8）式中的ημν（x）规定，且皆作为基本变量εμν（x）的泛函。对于统一理论的空时爱因斯坦张量，它的表式如下

方程（5.29）的意义在于，在该模式中，空时与引力虽然可以进行统一描述，但空时自身具有独立的演化机制，它是空时理论中的一组新方程，原则上可与引力物质状态无关。在宏观，空时M则是最小作用量原理支配下的动力学系统。对空时M这种演化机制的刻画，是该双变量理论的重要结果，也是它与广义相对论的重要区别。由这里可知，空时M的几何，是真正的空时几何（它不涉及引力）；而广义相对论中的所谓“时空几何”，实际上则应理解为描述的只是引力场的分布特征。

空时方程（5.29）和引力方程（5.21），是双变量理论描述宇宙中物质、引力和空时及其相互关系的两组方程。由引力方程（5.21）可知，宇宙中是物质决定引力，而并非是决定了空时。由空时方程（5.29）可知，空时除了其微观生成、演化受到量子力学原理支配外，它在宏观的行为将受到空间时间张量Θμν的决定。空时不仅与引力有不同的本源，与物质之间在本源上也是相互独立的。也就是说，在双变量理论目前体制下，并得不到空时是由物质决定的结论；而由空时与引力二者形成的绝对度量，将决定宇宙中物质的运动与演化。

对于空间时间张量Θμ，它与引力方程（5.21）中的质量张量Tμν类似，将作为产生空时度量扰动εμν的源而存在。从根本上讲，张量Θμν将与时空节律相关，它是节律S当世界坐标化后在空时方程中的体现。张量Θμν的表式将来源于创生空间与时间的宇宙中更为原初的基因，以及这种基因泄露在宏观世界中对空时的支配信息。张量Θν以及普适方程（5.29）的出现，将在广义相对论无法力及的范围，全面地打开世界M的另一片天地，为彻底地揭示和演绎空时自身的万千性状开辟道路。不难知道，是空间时间张量Θμν在撑控着宇宙空时行为最终的和自然的“天机”；质量张量Tμν，则是Θμν的寄驻“伴者”。

我们这里指出，对空时与引力不进行分离表述，就不可能彻底地了解空时与引力。而分离表述时，认为空时的度量是保持不变的，这与广义相对论的空时观并无根本区别。只有对空时自身度量的可变性进行开放式探索，才是对空时不附加条件的自然描述。一个彻底的空时、引力与物质的理论中，空时从本源上是与后二者独立的。显然，Minkowski的空时M'，只是这种一般空时M的一个特例，并是空时度量方程（5.29）的一个平庸特解。