救援路线并行搜救算法-海洋大数据

在海洋灾害中基于地理信息数据，实现快速并行搜救路线的生成是辅助决策系统应用的重点，本节介绍实际应用的可用于风暴潮灾害中并行搜救最佳调度算法。

1）问题具体描述和理论抽象

从计算机图论的角度来看，定义受灾区域为一个图G= （V，E），Vi为各个节点，表示灾民聚集点，每一边Eij=［Vi，Vj］有一个非负权值W（E）=Wij，表示节点Vi与节点Vj之间的路径长度。那么所求得的最小生成树就应该是图G的一个子图G* =（V*，E* ），且V=V*，E包含E * ［10］。

图5-22　无向图G

如图5-22所示，假设无向图G表示一个受灾区域，其中V1、V2、V3、V4、V5、V6分别表示6个人口聚集地，E12 、E23、…、E56为两个人口聚集地之间的路径，权值表示路线耗时。以虚线表示边意味着该边尚未加入到最终的结果E*当中。此例中，E12=15，E13=9，E14=2，E23=14，E34=7，E35=4，E45=6，E46=7，E56=3。

在计算机中存储此问题时采用矩阵存储法，所有节点两两之间的关系用n×n阶矩阵R0表示，若0表示某一点与它本身的关系表示两点不直接相连，即没有关系。R是一个对称矩阵，研∞究时只取其上三角矩阵记作R。根据树图的定义，易知n个点的无圈连通图有n—1条边，又因为最小生成树是所有边长之和最短的树图，易知这n—1条边对应上三角关系矩阵中的n—1个尽可能小的数。

在辅助决策系统中，灾后搜救需要对受灾区域进行全面快速的搜查，而Prim算法求得的最小生成树只方便用于在搜救队伍集体行动不分开的情况下进行搜救路径的选择，但是显然这样效率不够高，试想如果某受灾地仅需要50人进行搜救，而100人的搜救队伍中另外一半救援人员则可能因交通拥挤等客观原因无法高效率工作，对整体救援工作的进展也是有影响的。面对这个问题，对Prim算法进行了改进，使最终结果为两个子树，并在整体上达到路径耗时最少，从而提高搜救工作的效率［10］。

2）并行搜救最佳调度算法的提出

在风暴潮灾害辅助决策系统中，需要实现灾害发生后的调度功能，对受灾区域进行搜救是灾后救援行动的重中之重，如何规划搜救队伍的最佳搜救路线显得更为重要，尤其在受灾区域因灾害造成道路损坏以至交通不便时，就不能使搜救队伍一拥而上，以防搜救行动效率过低。

并行搜救最佳调度算法是针对搜救队伍分头行动的特殊情况产生的，它建立在Prim算法的基础之上，所得结果为两个子树G1* =（V1*，E1* ），G2 * =（V2*，E2* ），分别对应每支搜救队伍的路径图。这里以细实线表示G1，黑实线表示G2。算法具体步骤如下：

（1）找出图G=（V，E）中每个节点所有邻边的最小权值，如图5-22所示。

节点V1对应E12 、E13 、E14三条边，其中权值最小为2；节点V2对应E12 、E23两条边，其中权值最小为14；依此类推，求得表5-10。

表5-10　各节点对应其邻边的最小权值

(www.xing528.com)

（2）根据表5-10，选得最小权值中的最大值14，将此边E23加入到结果子树G2*的边集E2*中，V2、V3加入到结果子树G2*的节点集V2*中。如图5-23所示。

图5-23　步骤（2）

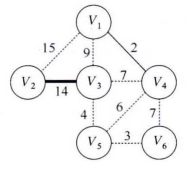
图5-24　步骤（3）

（3）根据表5-10，选得最小权值中的最小值，判断其邻接两节点是否在V2*中。若在，则找次小值接着进行判断；若不在，则将此边及节点加入到结果子树G1*中的边集E1*及节点集V1*中。如图5-24所示。

本例中，由表5-10可知，最小权值的最小值为2，其邻接两节点V1、V4不在V2*中，因此，把节点V1、V4加入G1*的V1*中，把边E14加入到G1*的E1*中。

（4）针对每个孤立点连接到两个子树的距离，判断其加入各自最近子树以后子树的总路径长度，取较小者将结果加入。如图5-25所示。

本例中，V5、V6为孤立点，V5加入G2*路径中，加入后的G2*总路径长度为E23 +E35 =18； V6加入G1*路径中，加入后的G1*总路径长度为E14+E46=9。比较得知应取V6加入G1*的结果集。

图5-25　步骤（4）

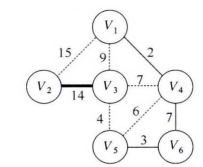
图5-26　最终结果图

重复步骤（4），直到图中无任何孤立点存在。

本例中，还剩余V5为孤立点，其加入G2*后总长度为18；加入G1*后的总长度为E14+E46+E56 =12。比较得知应取边E56加入G1*的结果集中。最终结果如图5-26所示。