时间序列相似性分析：海洋大数据

时间序列是指随时间变化的序列值或事件。在海洋研究领域存在大量的时间序列数据，如各类海洋传感器监测数据、海洋遥感影像、气象卫星云图等。传统的时间序列分析方法以模型分析为主，但模型分析方法建立在假设理论和数学基础之上，每一种模型都有其适用条件，因而在实际运用中具有一定的难度和局限性。数据挖掘（data mining）方法的产生弥补了以上的不足，它可以从大量、复杂甚至含有噪声和模糊的实际数据中，提取出一定的有用规则，不需要事先知道数据的分布情况，且得到的知识和信息也往往是单纯利用模型分析方法所无法得到的。时间序列数据挖掘（time series data mining，TSDM）应运而生，并成为数据挖掘领域一个重要研究方向。

时间序列相似性分析是时间序列挖掘的一个前期步骤，是时间序列分析的一种重要手段，其中的相似性匹配技术是时间序列模式匹配、模式分类与聚类、时间序列异常检测以及时间序列预测等各类时间序列数据挖掘方法的前提和基础。在时间序列相似性分析中，有两个关键问题，即时间序列表示和时间序列相似性匹配。

1）时间序列表示

直接将时间序列的数据按照它们各自的产生顺序排列即得到时间序列的一种表示，但时间序列挖掘领域一般将一条长度为n（n ＞ 0）的时间序列看作n维向量空间中的一个点，当前的高维数据索引方式难以应对这种情形。时间序列数据具有高维特点，如果直接进行相似性比较，则效率较低，且容易引起“维数灾难”问题，同时，这些高维数据中可能包含大量的与关键特征或模式无关的信息和冗余信息，这些信息会极大地降低算法的性能。因此，通过对时间序列的再表示可以起到降维的作用，除此之外，时间序列的再表示还具有降噪和归一化操作两个方面的作用，对于数据挖掘十分必要［14］

时间序列表示方法分为时间域连续性表示和基于变换的表示两大类。时间域连续性表示方法包括：逐段线性近似（PLA）、逐段聚集近似（PAA）、适应性分段常数近似（APCA）、符号聚集近似（SAX）、分段线性表示法（PLR）

基于变换的表示方法一般是指时间序列数据由时域到频域的变换。应用比较广泛的算法有离散傅里叶变换（DFT）、离散小波变换（DWT）、奇异值分解（SVD）等。基于变换的方法在采用某种变换方式将数据从时域变换到频域后，从变换后的系数中选取k（k＞0）个组成新序列来近似模拟原始序列，从而达到时间序列降维的目的。在实际应用中，基于DFT的表示可能会忽略信号的局部差异，因此适用于比较平稳的时间序列；小波变换可以保留数据的局部特征，但是其基函数不平滑，可能一段短时间序列在变换后得到大量系数，对系数的选取有很高要求，需要有较高理论基础；SVD方法是将原时间序列分解到k维空间，达到数据降维的目的，但是在产生基向量的过程中数据操作比较复杂。

2）时间序列相似性匹配

时间序列相似性匹配问题最早是由Agrawal等在1993年提出的，这一问题被描述为给定某个时间序列，要求从大型数据集合中找出与之相似的序列。时间序列相似性匹配算法有子序列和全序列匹配两种方式。时间序列相似性匹配的基础是时间序列相似性度量，使用哪种距离函数来度量两个时间序列是否相似是研究的关键，在不同领域甚至在同一领域，若给定的数据性质不同，则选取的距离函数可能也不同。常用的相似性距离度量方法主要有Lp距离法、动态时间弯曲 （DTW）法等。

Lp距离法最为常见，用于计算数值型表示的时间序列相似性程度，即利用距离公式计算两个时间序列的相似性。一般来说，距离越短，相似性程度越高。距离函数中常用的有三种，分别是曼哈顿距离、欧氏距离和最大距离。上述表示方法也存在一定的局限性：首先要求两时间序列的长度是相等的；其次由于是通过多点间的距离度量两者的相似度，因而时间序列的波动范围差异及噪声会对距离产生很大影响，利用这种度量方式之前需要对时间序列数据进行预处理，如降噪或归一化处理等。

DTW法与距离法最大的不同在于它可以处理非等长时间序列之间的相似性度量。由于时间轴的微小变形将会引起欧氏距离很大的变化，因此对于时间轴有轻微变形的时间序列相似性度量，距离法将不再适用。DTW法可以归结为用动态规划算法寻找一条具有最小代价的最佳路径。这种距离对于时间轴的缩放不再敏感，但是会对幅值的位移变形和幅值按比例缩放敏感。该方法的缺点在于时间复杂度较高，需要计算最短路径和距离矩阵。

3）时间序列相似性匹配算法在数字海洋风暴潮辅助决策系统中的应用

时间序列相似性匹配已经应用于很多领域，如股票交易分析、天气预报等，在海洋防灾减灾领域，可用于风暴潮辅助决策，即在风暴潮数据序列中通过相似性匹配算法找到与查询序列相似的序列，再依据此序列所处的灾害等级和处理方法，来判断该次风暴潮所处的等级以及给出合理的解决方案。风暴潮数据库记载了以往发生风暴潮的编号、时间、地点、成因、成灾范围、受灾人数、死亡人数、灾度评估、台风描述、救助等信息。由于风暴潮时间序列具有非线性、数值与事件相混淆的特征，因此需要给出合适的风暴潮序列相似性定义、度量模型和匹配算法。文献［15］提出了基于斜率特征向量过滤的风暴潮序列相似性匹配算法（FBCM Slope）。

（1）风暴潮序列的相似性定义。设Q和C是两个不同的风暴潮序列，x和y分别为两序列中的元素，用函数δ（x，y）来定义其相似性，有

δ（x，y）=1，若|x（t）—y（t′）|≤ε

δ（x，y）=0，若|x（t）—y（t′）|＞ε，或者x（t）=0，或者y（t′）=0

式中，ε为误差阈值，由用户根据具体要求和实验确定。ε值与风暴潮的相似成反比，即ε的值越小，表明两序列的相似度越高；反之，则认为两序列相似度越低。上述函数δ（x，y）=1的时候，认为x和y是相似的；反之则不相似。

两个风暴潮序列的相似性度量模型定义为

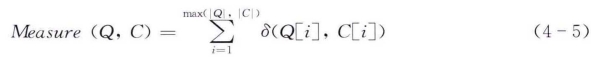
若|Q|=|C|，则两序列的长度相等。(www.xing528.com)

（2）相似性匹配算法。基于斜率的分段算法：把风暴潮序列按时间量化，记为（xi，yi），xi为按照时间顺序记录的第i次风暴潮发生的时间，为一个（1，2，3，4，…，n）数组，每一个数字代表某次风暴潮发生的时间（年月日），yi为对应的数字发生该次风暴潮的最高潮位。如风暴潮时间序列数据库是从1949年7月24日开始的，最高潮位为519 cm，则记为（1，519），依此类推。

风暴潮序列在坐标系中的表示：xi记为x坐标，yi记为y坐标，依次把时间序列对应在相应的坐标系内。每两个相邻的时间序列点用垂线隔开，趋势上升记为“1”，趋势下降记为“0，则序列可以用“0”“1”组成的长度为|S|-1的二进制比特表示，如图4-3a所示，特征向量值为“111001110011100”。这种方法的优点是算法效率高、简单，但不适用于含噪声值的时间序列。如图4-3b所示，含有a、b、c、d四个噪声值，从而导致剔除掉正确的时间序列。

为了缓解序列噪声值，提高精确度，采用基于斜率的特征序列表示法：给定时间序列S=S（s0，s1，s2，...，sn-1）和分段参数l（假设l能被n-1整除），将序列S分割成l段，即s0，s1，s2，…，sl-1。令j =（n-1）/l，每段包含l+1个点（包含两边端点），表示为Si =（si，j，…，s（i+1），j）（0 ≤i ＜l-1）；令

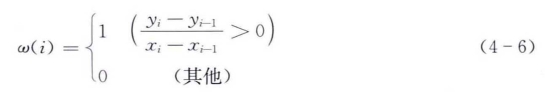
图4-3　序列特征值的分段表示［15］

当时，表示时间序列Si在第i段是上升的，即二进制数记为“1”；否则，认为该段时间序列是下降的，记为“0，最后形成一串由0、1组成的形状特征值。

这里采用全序列匹配方法，只要两个序列的特征向量相同，则认为是相似的。因此经过特征向量值的相似匹配过滤，可以剔除掉一部分风暴潮序列。这样不仅节省了空间，且计算比较简单，只需一次遍历就可以计算出所有时间序列的特征值。

具体算法步骤如下：

①数据预处理。把风暴潮数据库中的数据按照时间顺序剔除掉编号、时间、地点、成因、成灾范围、受灾人数等，并将对应的台站潮位信息放入预处理结果文件中。

②构造风暴潮序列。从预处理结果中，把各个台站的潮位信息按照时间顺序编号，依次放入数组中，形成一组风暴潮序列SUS。

③监测台站数据的处理。把监测到的台站数据按照时间顺序，依次把描述信息等按照第①步进行预处理，然后按时间顺序放入数组中形成时间序列数据。

④查询序列与数据序列的相似匹配。具体描述如下：根据检测到的台站数据，经过第③步处理，作为查询序列，与风暴潮数据库中的序列进行基于斜率的分段相似匹配。若相似，则放入过滤数据库中，然后利用定义的相似度量模型，进行进一步的风暴潮序列相似性度量，与误差阈值ε相比，若小于ε值，则认为与该风暴潮序列相似。若有多条，则认为与最相近的序列为相似序列。

⑤风暴潮辅助决策。依据第④步得出的相似序列，在风暴潮灾害数据库中搜索出该次风暴潮发生的等级和处理方法，领导者或者决策者可以根据等级和该次处理方法来辅助决策此次风暴潮的发生。

（3）实验及结果分析。把1949-2008年中随机抽取的10组数据序列作为查询序列，与数据序列的风暴潮序列进行相似匹配。分段过滤算法的l值选取在实验中占有非常重要的地位。经过多次实验，l值选取7是最佳的，既没有过滤掉相似的序列，也有效地剔除掉了一部分序列。图4-4是从多组实验中抽取的一组实验。

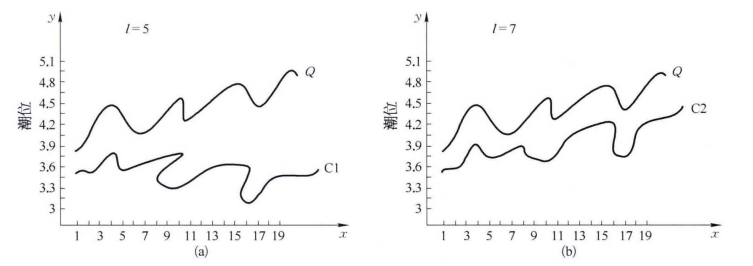
图4-4　l取值不同时对比［15］

图4-4中查询序列Q是从数据序列中抽取的编号为H01012的风暴潮序列，C1、C2分别是在数据序列中找到的编号为H01016、H01123风暴潮序列。经过相似度量模型计算，当l=7时，Measure=0.000 52；当l=5时，Measure=0.009 56，都比选定的阈值ε=0.01小，而且从图4-4中可以明显地判定出，当l=7时，在数据序列中找到的风暴潮序列与序列Q匹配程度更高。