土体中水相的流速与其水力梯度成正比,服从Darcy定律
![]()
式中 vw——水相的流速,或水流通量;
kw——水相渗透系数,代表当水力坡度为1时液体在土体的渗流速度,单位为长度/时间,如m/d(或cm/s);
∂hw/∂y——y方向的水力梯度,∂hw/∂y=iwy。
水相的渗透系数kw取决于流体的性质和孔隙介质的性质。不同类型的流体(密度及黏度不同)或不同类型的土(黏土、粉土或砂土)具有不同的渗透系数kw值。
Darcy定律用于描述稳定的层流渗透规律,但当渗流速度达到一定值后层流就会向紊流转变,除产生黏滞阻力外,还会产生较大的惯性阻力,此时水流通量与土水势梯度不再呈线性关系,Darcy定律不再适用,此时的渗流速度即为Darcy定律的临界渗流速度;另外,当渗透速度很低时也会偏离Darcy定律,这说明有Darcy定律在使用时存在上限和下限(王勇等,2009)。
饱和土中水相的流动服从Darcy定律,对某特定的饱和土,其水相渗透系数kw接近于常数。水相在非饱和土中的流动也符合Darcy定律。Childs和CollisCeorge(1950)研究表明,在一特定含水率下,通过非饱和土的水相流速与土水势梯度呈线性比例关系,水相渗透系数为常数,这与饱和土的情况相同。
Richards(1931)扩展了Darcy定律,用以描述非饱和土中水相的运动规律,即广义Darcy定律
![]()
式中 vx、vy、vz——非饱和土中三个方向的水相流速,即单位时间内通过单位截面积的水相流量;
Ψ——土体土水势;
∂Ψ/∂x、∂Ψ/∂y、∂Ψ/∂z——x、y、z方向的土水势梯度。
将式(2.2)代入水流连续方程,得
![]()
式中 θ——土体的体积含水率,可表示为土体中水的体积与土体的总体积之比,即θ=vw/v=nSr。
体积含水率θ与质量含水率w(土体中水质量与干土质量重的比值,w=mw/ms)之间有如下换算关系
![]()
式中 ρd——土体干密度;
ρw——水的密度。
Liakopoulos(1965)发现天然沉积砂的饱和度或体积含水率与基质吸力间关系表现出明显的滞回现象,水相渗透系数与体积含水率与饱和度是直接相关的,因此,水相渗透系数与基质吸力间关系也有着明显的滞回,但水相渗透系数与体积含水率间的关系没有滞回现象,如图2.2所示。
非饱和土的水相渗透性远比饱和土复杂。首先,非饱和土保持水分的能力与它的吸力有关;其次,在非饱和土中水相渗透系数不是常数,而是随土样吸力或含水率的变化而变化;最后,非饱和土的水相渗透性与土体孔隙的弯曲因子(Tortuous Factor)有关,非饱和土孔隙的弯曲因子又直接与应力状态、土体吸力和土体结构有关(徐永福等,2005)。
非饱和土水相渗透系数还与击实条件、黏土含量和液塑限等因素有关,除此以外还与有效应力、水头梯度和饱和度等因素有关,分别解释如下。(https://www.xing528.com)
在饱和土中,渗透系数是孔隙比的函数,孔隙比与有效应力直接相关,随着有效应力的增加而减小。有效应力对饱和土渗透系数的影响可归结为有效应力对孔隙比的影响。对于非饱和土而言,有效应力不仅影响土体的孔隙比,而且对孔隙弯曲因子也有影响(徐永福等,2005)。
Dunn(1984)研究发现水相渗透系数会随着水头梯度的增加而减小。水头梯度增加引起水相渗透系数减小的原因主要有:①水流拖曳力增加使得土粒移动堵塞水流通道;②土体产生附加固结变形,孔隙比减小;③改变土体空间结构,使土粒定向排列。而Imamura等(1996)认为水头梯度增加会使土体中产生管涌现象,细颗粒被冲刷流走,使土体水相渗透系数增加。
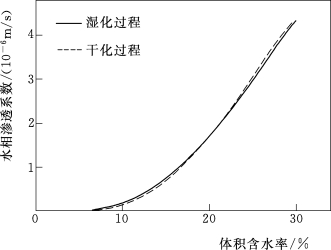
图2.2 水相渗透系数与体积含水率间的关系曲线(Liakopoulos,1965)
非饱和土水相渗透系数还受土的饱和度(或含水率)变化的影响。非饱和土孔隙比对水相渗透系数的影响可能不明显。但是,饱和度变化对其的影响则十分显著(Fredlund和Xing,1994)。由于液体只会通过被液体所充填的孔隙空间流动,因此被液体充填孔隙的比例是非常重要的因素。当一种土变成非饱和时,空气首先取代某些大孔隙中的液体,导致液体通过较小孔隙流动。土的基质吸力的进一步增加导致液体占有的孔隙体积进一步减少,气水界面越来越靠近土颗粒,使得水相渗透系数随着可供液体流动的空间减少而急剧降低。另一种解释为饱和度低,孔隙中的气占据了较大的体积,阻碍液体的流动,过水断面面积也缩小,水相渗透系数相应减小。总之,非饱和土的水相渗透系数随其饱和度的减小而减小。
由式(2.3)可知,土体为饱和状态时,∂θ/∂t=0,水相渗透系数kw为常数。土体为非饱和状态时,水相渗透系数kw与体积含水率θ或吸力s有关,通过试验曲线拟合出经验公式,常用的形式有
![]()
式中 s——土中的吸力;
θs——饱和土体积含水率,θ/θs=Sr;
n、a、b——试验测定的经验参数;
ks——饱和土渗透系数。
Xu和Sun(2002)亦推导出非饱和土的水相渗透系数kw与饱和土的渗透系数ks之间的关系为
![]()
式中 Se——有效饱和度,Se=(Sr-Sres)/(1-Sres),Sr和Sres分别为饱和度和残余饱和度;
λ——与土体孔径分布指标有关的常数。
由式(2.5)、式(2.6)可见,非饱和土的水相渗透系数与土体的饱和度、体积含水率和吸力有关,随着饱和度、体积含水率的增加呈几何级数增加趋势。
非饱和土水相渗透系数的确定比饱和土的要复杂。可以通过间接方法确定非饱和土的渗透系数,即由测出的基质吸力与饱和度关系曲线得到土体孔径大小分布,再用经验公式计算得到非饱和土水相渗透系数的近似值(Ng和Pang,1999)。Xu和Sun(2002),Xu和Dong(2003)用分形理论描述了非饱和土的孔径分布特征,导出了符合各类非饱和土常规渗透试验结果的渗透系数理论公式。用间接方法获得非饱和土水相渗透系数近似值依赖于所用的经验公式,相同的土体采用不同的经验公式得到的水相渗透系数差别会很大。
也可以通过非饱和土渗透试验直接测量非饱和土水相渗透系数,但试验耗时较长。在直接量测过程中,水力梯度可以保持为常数,也可以随时间变化。相应地,试验方法亦可分为两类,即稳态试验方法(流速不随时间的变化而变化)和非稳态试验方法(流速随时间的变化而变化,其代表方法为瞬时截面法)。
在稳态法中,流经试样的流量、水力梯度和含水率等是常量,不随时间变化;而非稳态法中上述参数为变量。稳态法假定Darcy定律在非饱和状态下也有效,一定吸力或饱和度对应的水相渗透系数可通过相应的流量和水力梯度计算(Huang等,1998;赵彦旭等,2010)。非稳态法中的瞬时截面法通过测量一维渗流状态下流量和含水率的时间与空间剖面,求解瞬态流控制方程,得到非饱和土水相渗透系数。
稳态法测量范围小,其测量范围为10-1~10-8cm/s。对于黏土含量不高的天然土样,其渗透系数一般大于10-8cm/s,可以选用稳态法来测量其水相渗透系数,既具有较高的测量精度,又能满足实际工程的需要。非稳态法测出的水相渗透系数精确度要低一些,但测量范围大,水相渗透系数的量测范围为10-1~10-13cm/s。
稳态法所用试验装置与饱和土常水头试验相似,主要区别是增加了气压控制装置,为了能将水压和气压分开,还设置了陶土板。该方法适用于水相渗透系数较大的非饱和土。徐永福等(2005),邵龙潭等(2005),赵晓霞(2010)和王念秦等(2014)先后研发了非饱和土稳态渗流试验装置。而对于水相渗透系数较低的黏土,水相渗透系数测试过程中,液体出流量很少,不仅试验时间长,而且对出流液体体积的量测精度要求高,同时还要防止出流液体的蒸发。为量测这类非饱和土的水相渗透系数,通常采用非稳态的方法。瞬时截面法是一种常用的非稳态方法,可用于实验室或原位试验。王文焰等(1990)研制了一种用马氏容器供水的非饱和土水分运动参数测试设备,陈正汉等(1993)用该设备测定了非饱和黄土的水相渗透系数;高永宝等(2005)利用水气运动联合测试仪量测了一定湿密状态下黄土的渗透特性;王铁行等(2008)采用水平土柱入渗法得到了压实黄土的水分扩散率与体积含水率的关系,分析了黄土水相渗透系数随干密度和含水率的变化规律;叶为民等(2009a)采用瞬时截面法研究了侧限状态下非饱和高压实高庙子膨润土的水相渗透特性;李旭(2014)采用湿润锋前进法和瞬时截面法计算了砂土、粉土、黏土三种土体的非饱和水相渗透系数函数;文杰等(2015)用原位瞬时截面法处理黄土地区降雨入渗监测数据,得到非饱和黄土的水相渗透系数与体积含水率之间的关系。
Gardner方法和θ法也可以用来确定水相渗透系数。Gardner(1958)提出了基于Richards控制方程的测量技术。施加某一气压时,吸力有一增值,在此增值的作用下,土样开始脱水,试验过程中,跟踪排水量随时间的变化,假设所加吸力增量足够小,可以认为弥散度在排水过程中为常数,再通过对Richards方程的简化应用获得水相渗透系数。Libardi等(1980)提出了一种测定非饱和土水相渗透系数的方法,即θ法,该方法假设蒸发及入渗作用微弱,地下水的重分布只受到重力场的作用。假定土体在某深度以上的平均体积含水率与该深度处的体积含水率线性相关,由水相渗透系数与体积含水率的函数关系得到非饱和土水相渗透系数。
稳态法和非稳态法中的瞬时截面法是非饱和土水相渗透系数测定试验中较常用的方法,以下分别进行介绍。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




