值得指出的是,由图10.4可直观判断出对桩基非线性动力响应有显著影响的关键参数及影响微小的次要参数。确定出系统动力响应的关键参数后,可通过调整关键参数值实现动力参数设计,使得桩基的非线性动力响应特性达到预期目标。为完善参数影响效应研究,基于图10.4的结果,挑选桩基的抗压刚度EA和弹性地基的Winkler参数k0为变化参数,通过桩基的主共振响应变化研究参数对系统非线性动力响应的影响[95]。
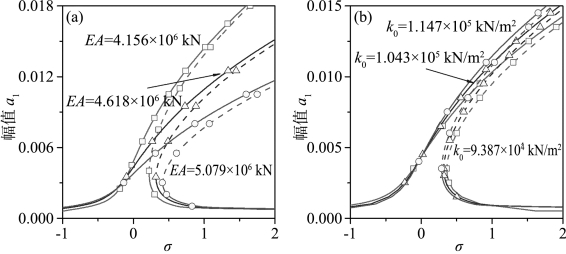
图10.5 参数对于自由-铰支桩基主共振幅频响应的影响对比
(a)桩基抗压刚度EA;(b)弹性地基Winkler参数k0
图10.5给出了自由-铰支桩基的主共振幅频响应曲线,其中图10.5(a)和(b)反映出显著参数及非显著参数对非线性动力响应的影响。由图10.5(a)可知,随抗压刚度EA增强,幅频响应的共振区域及多值区域变化不大,但响应的硬弹簧特性愈发显著。而且,不同抗压刚度对应的幅频曲线在高响应幅值时差异较大。然而,当调整弹性地基Winkler参数k0的值时,主共振响应的幅频曲线变化并不明显。但应注意到,弹性地基Winkler参数k0的增长会引起非线性响应硬弹簧特性的减弱,特别是在响应幅值较高时这种现象更明显。对比图10.5(a)和(b)可知,由Pareto图判定出的不同影响效应参数对桩基动力响应影响不同,且标准化效应显著的因素为关键参数,在工程实践中对其进行合理调整更易于得到理想结果。(https://www.xing528.com)
为完善研究内容,图10.6给出了自由-自由桩基的主共振幅频响应曲线。由图10.6(a)可知,抗压刚度对有效非线性系数标准化效应的减弱导致该参数对系统主共振响应的影响也减弱。显然,三种情况的骨架曲线间差异并不是特别显著。然而,抗压刚度增大导致共振区域减小,并使得响应幅值及多值区域均有明显减小。由于桩端约束对系统动力响应的影响,弹性地基Winkler参数k0对共振响应的影响进一步弱化,三种情况间幅频响应差异微弱(见图10.6(b))。
综上所述,数值结果证实在确定的目标响应情况下,由Pareto图直观反映出的各参数影响效应可用于指导动力参数设计。而且,通过统计分析方法得出的显著效应参数可作为设计中的敏感参数。对敏感参数进行合理的调整,可以在最节省的情况下迅速达到调整动力响应的预期目标,并实现对于动力系统的参数设计。
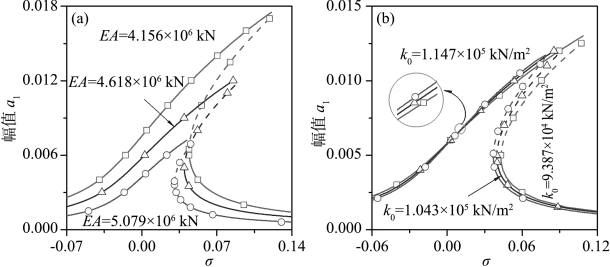
图10.6 参数对于自由-自由桩基主共振幅频响应的影响对比
(a)桩基抗压刚度EA;(b)弹性地基Winkler参数k0
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




