与试验研究相对应,为深入分析各参数对系统各项性能的影响,在理论分析时也需在合理的参数范围内充分分析各参数效应。为全面合理分析各参数对结构动力响应的影响,首先需要对分析过程进行参数设计试验,即设计出既全面又合理的参数组合,并对其结果进行分析。总体而言,在进行统计分析计算时,常用的试验设计方法有:正交、均匀试验设计方法,单纯形、双水平单纯形优化方法,回归正交设计方法和序贯试验设计方法等。结合本章研究结构动力响应的特点,选择运用正交试验设计方法收集结构物的各关键参数对动力响应目标函数影响的数据。
另一方面,作为数据收集的一种常见手段,试验设计通常是参数分析的基础,也是数理统计的重要分支。对于多参数分析而言,正交试验设计(OED)是一种实用的试验设计方法。实际这种方法也是遗传算法的一个特例,在科研和实践中被普遍应用[90]。值得指出的是,对参数设计的全体因素而言,正交试验是一种部分试验,但是对多参数中的某两个参数而言,正交试验又是一种全面试验(等重复)。在本章中,为了选取最少的数值计算量并达到全面收集数据的目的,本章的参数设计研究基于正交试验设计进行参数数据收集。
正交试验设计是适用于多因素多水平参数研究的一种设计方法,其运用正交性挑选出具有代表性(等差散布、均匀可比)的特征参数点进行试验,且具有高效、经济的特点。为便于进行正交试验设计,日本学者提出了正交试验表用于进行参数组合分析。运用多参数的排列组合,正交试验表可极大地减少试验工作量。另一方面,可以根据研究对象参数的特征,选取合理的正交试验表,而且目前已有多种正交表可供查询和应用。正交表可表示为Ln(tc),其中L为正交符号;n为进行试验次数;t表示试验中各因素的状况(称为水平);c为正交表列数,即试验研究过程中的参数个数。例如L9(34)表示该正交表需做9次试验,在试验过程中研究4个参数,且各参数均为3水平。(https://www.xing528.com)
表10.1 L9(34)正交试验表
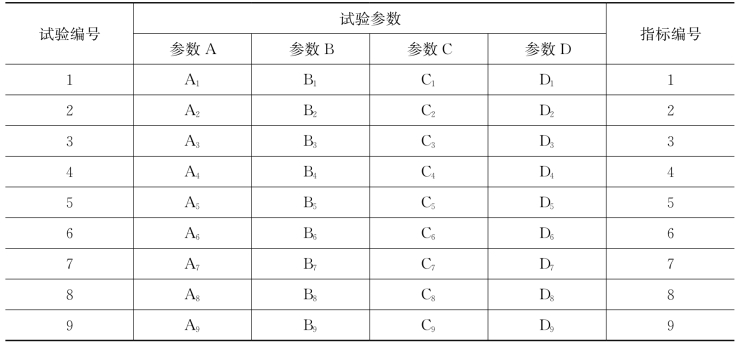
其中,A(B,C,D)i(i=1,2,3)表示参数的水平。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




