【摘要】：忽略式中的外激励项、阻尼项和非线性项，可以得到不可伸长桩基线性自由振动方程。为了讨论桩基的线性响应以及地基模型的影响，接下来分析不同地基模型支承桩基的固有频率及模态。基于给定的桩基物理参数，表7.1、表7.2和表7.3分别给出三种约束桩基的前六阶固有频率。值得指出的是，对于自由-固支约束，引入剪切参数K1可能导致桩基低阶频率减小而高阶频率增大。
忽略式（7.1a）中的外激励项、阻尼项和非线性项，可以得到不可伸长桩基线性自由振动方程。对比不可伸长弹性地基梁的线性自由振动方程（式（3.3）），两者在形式上并不存在明显的差别，两者的固有频率和模态基本相似。为简便起见，本节忽略相应的求解过程。另一方面，选取弹性地基物理参数：Es=23.94 MPa，νs=0.2，ν=0.25；桩基的物理参数：长度l=6.096 m，半径R=0.243 m，密度ρ=2.403×103kg/m3，弹性模量E=2.482×104MPa。
为了讨论桩基的线性响应以及地基模型的影响，接下来分析不同地基模型支承桩基的固有频率及模态。根据工程中细长桩的约束情况，假设桩基上端无约束，而下端约束分别可取为固支（嵌岩桩）、铰支（弹性地基刚度较大情况）和自由（一般性的细长桩）等情况。
基于给定的桩基物理参数，表7.1、表7.2和表7.3分别给出三种约束桩基的前六阶固有频率。总体而言，由于Winkler参数K0远大于剪切参数K1，因此，桩基的固有频率主要由Winkler参数K0确定。然而由于第二弹性层的引入，三参数地基模型导致Winkler参数K0的影响明显减小。值得指出的是，对于自由-固支约束，引入剪切参数K1可能导致桩基低阶频率减小而高阶频率增大。更为重要的是，当弹性地基刚度足够大时，桩基非线性响应可能存在1∶1内共振现象。
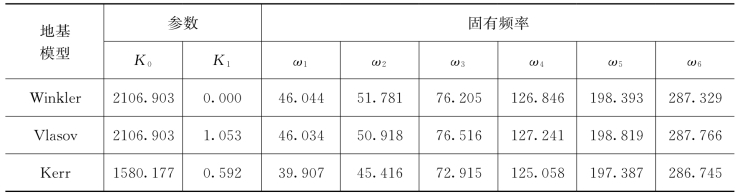
表7.1 地基模型对桩基频率的影响（下端固支）
(www.xing528.com)
表7.2 地基模型对桩基频率的影响（下端铰支）
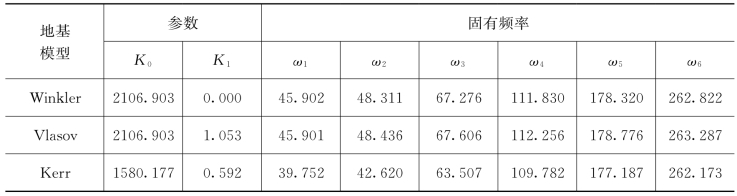
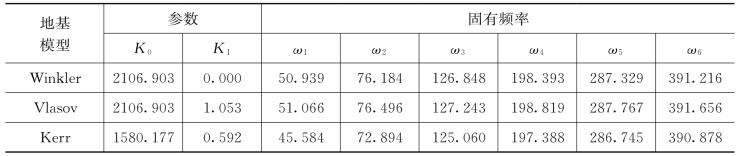
表7.3 地基模型对桩基频率的影响（下端自由）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
