地基模型对比研究：土-结构相互作用中的动力设计

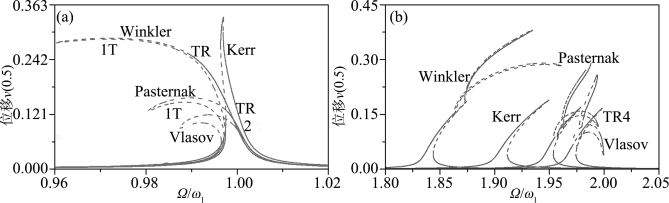
为了说明地基模型的影响，选取如下的参数值：n=3，Es=8.9 MPa，νs=0.2，ν=0.25，γ=1和p=0.10。图6.10分别给出地基模型对弹性地基梁在主共振区（Ω/ω1≈1.0）（图6.10（a））和亚谐波共振区（Ω/ω1≈2.0）（图6.10（b））内幅频响应曲线的影响。总体而言，地基模型参数K0和K1影响了弹性地基梁的固有频率以及用于确定离散模型系数的固有模态。因此地基模型明显影响弹性地基梁的非线性响应。从图6.10可以看出基于不同地基模型得到的幅频响应曲线呈现明显的不同。对于低阶模态，剪切参数Gp（弹簧系数c）对非线性响应起软化（硬化）效应。事实上，Vlasov模型得到了最强的软弹簧行为，相反Kerr模型得到了硬弹簧行为，如图6.10（a）所示。值得指出的是，目前已有的试验结果揭示了桩基的软化行为。因此从弹性地基这个角度而言，由二次弯矩导致的平方非线性可以为这种非线性行为提供较为合理的解释。相反对于高阶模态而言，这些影响基本可以忽略，如图6.10（b）所示。然而，地基模型仍然明显影响主共振区和2T周期解分支，并且在幅频响应曲线呈现出定性和定量的差别。

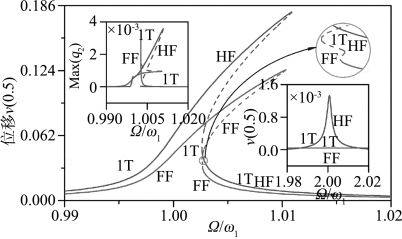
图6.9　铰支-自由梁和自由-自由梁的幅频响应曲线（p=0.10）

(www.xing528.com)

图6.10　地基模型对弹性地基梁幅频响应曲线的影响（p=0.10）

（a）Ω/ω1≈1.0；（b）Ω/ω1≈2.0

另外，值得指出的是幅频响应曲线中的动态分岔。实际上，由于较大的激励幅值，一些幅频响应曲线存在一些环面分岔点。然而，除了2T分支外，Kerr模型不能得到任何环面分岔。相反，由Vlasov模型获得的不稳定2T周期解通过环面分岔获得稳定，如图6.10所示。